二叉搜索树
前缀树

二叉树

  1. 翻转等价二叉树

    二叉搜索树

    image.png

    ×95.96.不同的二叉搜索树-

    （1）动态规划 叛徒

    image.pngimage.png ```python class Solution: def numTrees(self, n: int) -> int: store = [1,1] #f(0),f(1) if n <= 1:
    1.  return store[n]
    for m in range(2,n+1):
    1.  s = m-1
    2.  count = 0
    3.  for i in range(m):
    4.      count += store[i]*store[s-i]
    5.  store.append(count)
    return store[n]
  1. <a name="dCVrA"></a>
  2. ### （2）递归
  3. ![image.png](https://cdn.nlark.com/yuque/0/2021/png/1411624/1618306854731-f96bdf6f-a644-41b1-adf2-4f9914915921.png#height=31&id=HIB47&margin=%5Bobject%20Object%5D&name=image.png&originHeight=31&originWidth=425&originalType=binary&size=4367&status=done&style=none&width=425)<br />这道理搞清代码的逻辑关系最重要<br />![image.png](https://cdn.nlark.com/yuque/0/2021/png/1411624/1618307726965-a9a08fe3-fe99-4d7a-98fb-48df83ab5fa2.png#height=563&id=fnJYO&margin=%5Bobject%20Object%5D&name=image.png&originHeight=563&originWidth=842&originalType=binary&size=92724&status=done&style=none&width=842)
  4. ```python
  5. class Solution:
  6.     def generateTrees(self, n: int) -> List[TreeNode]:
  7.         if(n==0):
  8.             return []
  9.         def build_Trees(left,right):
  10.             all_trees=[]
  11.             if(left>right):
  12.                 return [None]
  13.             for i in range(left,right+1):
  14.                 left_trees=build_Trees(left,i-1)
  15.                 right_trees=build_Trees(i+1,right)
  16.                 for l in left_trees:
  17.                     for r in right_trees:
  18.                         cur_tree=TreeNode(i)
  19.                         cur_tree.left=l
  20.                         cur_tree.right=r
  21.                         all_trees.append(cur_tree)
  22.             return all_trees
  23.         res=build_Trees(1,n)
  24.         return res

√98. 验证二叉搜索树

image.png
可以利用中序遍历结果来进行验证 - 783二叉搜索树节点最小距离

  1. class Solution:
  2.     def isValidBST(self, root: TreeNode) -> bool:
  3.         self.vals = []
  4.         self.inOrder(root)
  5.         for i in range(len(self.vals)-1):
  6.             if self.vals[i+1]<=self.vals[i]:
  7.                 return False
  8.         return True
  10.     def inOrder(self, root):
  11.         if not root:
  12.             return 
  13.         self.inOrder(root.left)
  14.         self.vals.append(root.val)    # 中序遍历 得到的有序序列
  15.         self.inOrder(root.right)

×99. 恢复二叉搜索树（困难）

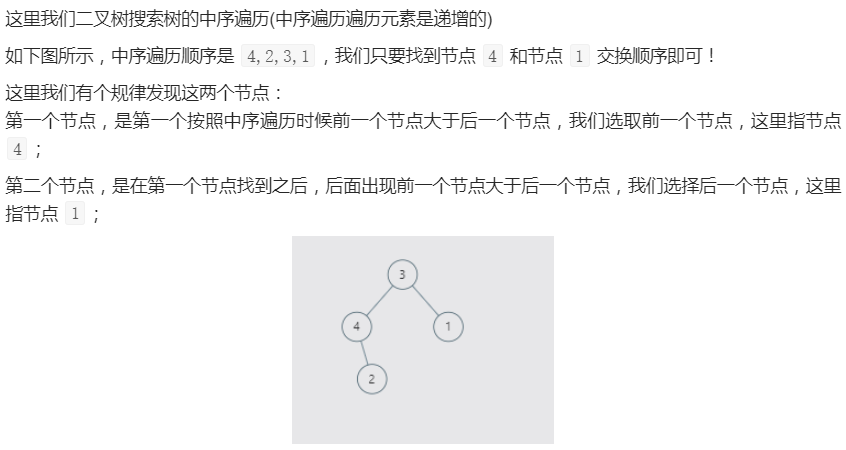
image.png

  1. class Solution:
  2.     def recoverTree(self, root: TreeNode) -> None:
  3.         self.firstNode = None  # 双指针
  4.         self.secondNode = None
  5.         self.preNode = TreeNode(float("-inf"))   # 负无穷
  7.         def in_order(root):
  8.             if not root:  # 终止条件
  9.                 return
  10.             in_order(root.left)
  11.             # 中序遍历
  12.             if self.firstNode == None and self.preNode.val >= root.val:
  13.                 self.firstNode = self.preNode
  14.             if self.firstNode and self.preNode.val >= root.val:
  15.                 self.secondNode = root
  16.             self.preNode = root
  18.             in_order(root.right)
  20.         in_order(root)
  21.         self.firstNode.val, self.secondNode.val = self.secondNode.val, self.firstNode.val

109. 有序链表转换二叉搜索树

173. 二叉搜索树迭代器

235. 二叉搜索树的最近公共祖先

√783. 二叉搜索树节点最小距离

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。
「二叉搜索树（BST）的中序遍历是有序的」

  1. class Solution(object):
  2.     def minDiffInBST(self, root):
  3.         self.vals = []
  4.         self.inOrder(root)
  5.         return min([self.vals[i + 1] - self.vals[i] for i in range(len(self.vals) - 1)])
  7.     def inOrder(self, root):
  8.         if not root:
  9.             return 
  10.         self.inOrder(root.left)
  11.         self.vals.append(root.val)    # 中序遍历 得到的有序序列
  12.         self.inOrder(root.right)

前缀树

×208. 实现 Trie (前缀树)

image.png
image.png

  1. class Trie:
  2.     def __init__(self):
  3.         self.d = {}
  5.     def insert(self, word: str) -> None:
  6.         t = self.d
  7.         for c in word:
  8.             if c not in t:
  9.                 t[c] = {}
  10.             t = t[c]        #字典迭代
  11.         t['end'] = True     #标记单词终点
  13.     def search(self, word: str) -> bool:
  14.         t = self.d     # 浅复制，b=a，接着对b所有的操作都会在a上也操作一次，如果不想这样，想让b，a没有关联就得import copy.deepcopy
  15.         for c in word:
  16.             if c not in t:   # 如果字典里没有这个字母，那一定搜索不到
  17.                 return False
  18.             t = t[c]  #  如果搜索到这个字母，接着后面搜
  19.         return 'end' in t
  21.     def startsWith(self, prefix: str) -> bool:
  22.         t = self.d
  23.         print(t)
  24.         for c in prefix:
  25.             if c not in t:
  26.                 return False
  27.             t = t[c]
  28.         return True
  31. # Your Trie object will be instantiated and called as such:
  32. # obj = Trie()
  33. # obj.insert(word)
  34. # param_2 = obj.search(word)
  35. # param_3 = obj.startsWith(prefix)

相关题型

211. 添加与搜索单词 - 数据结构设计

212. 单词搜索 II

421. 数组中两个数的最大异或值