动态规划基本框架
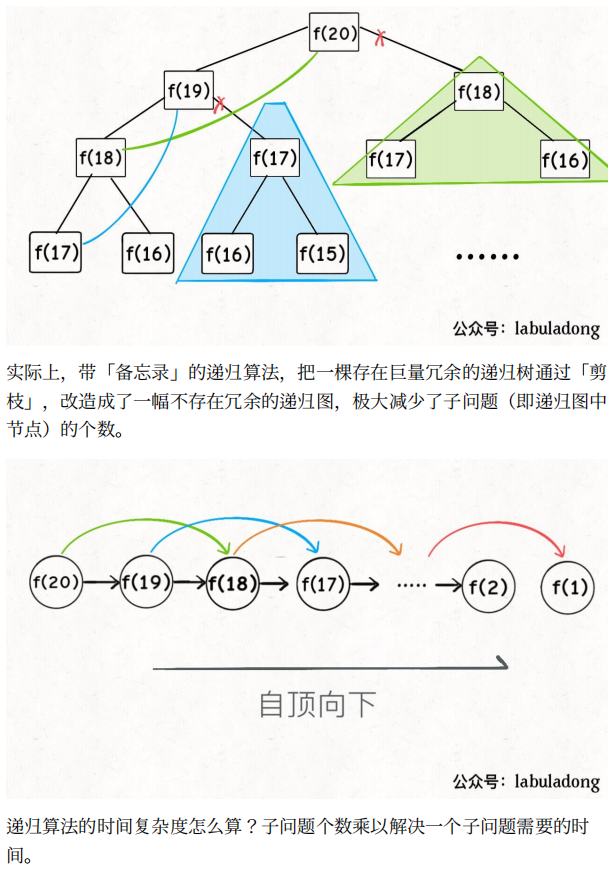
⼀、斐波那契数列

def fib(N:int):if N==1 or N==2 return 1return fib(N-1)+fib(N-2)



def fib(N):if N<1: return 0memo=[0]*(N+1)return helper(memo,N)def helper(memo,n):if n==1 or n==2: return 1if memo[n] != 0 : return memo[n]; memo[n] = helper(memo, n - 1) + helper(memo, n - 2); return memo[n]; }
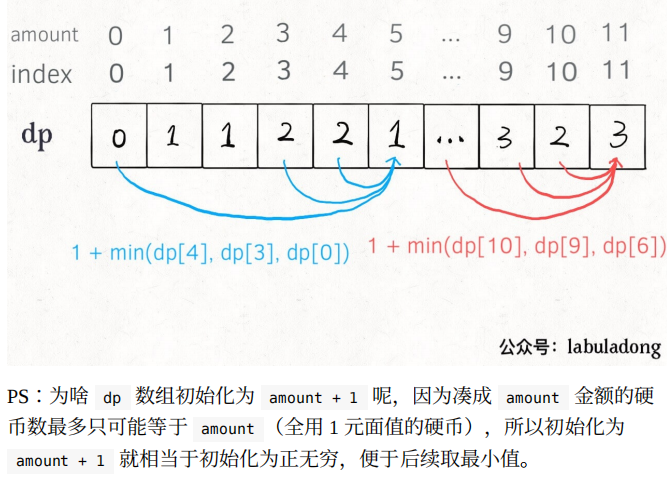
⼆、凑零钱问题

// coins 中是可选硬币⾯值,amount 是⽬标⾦额def coinChange(coins, amount):








def coinChange(coins,amount):dp=[amount+1]*(amount+1)dp[0]=0for i in range(amount+1):for coin in coins:if i-coin<0: contine # 跳出循环dp[i]=min(dp[i],1+dp[i-coin])return dp[amount]==amount+1 ? -1 : dp[amount] # 重点语句
三、最后总结
进阶答疑
一、最优子结构详解
1、最优子结构并不是动态规划独有的一种性质,能求最值的问题大部分都具有这个性质;但反过来,最优子结构性质作为动态规划问题的必要条件,一定是让你求最值的。找最优子结构的过程,其实就是证明状态转移方程正确性的过程,方程符合最优子结构就可以写暴力解了,写出暴力解就可以看出有没有重叠子问题了,有则优化,无则 OK。
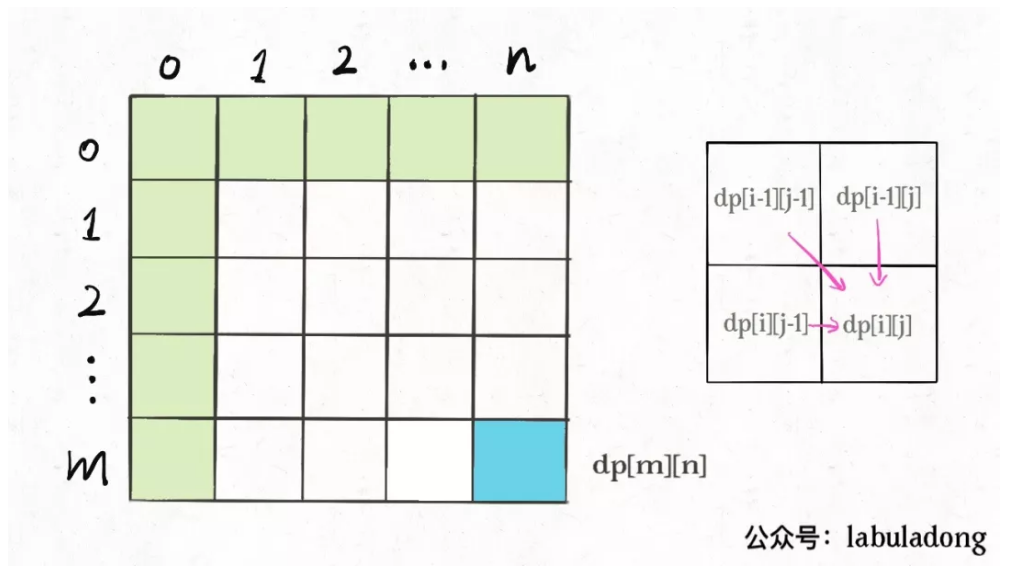
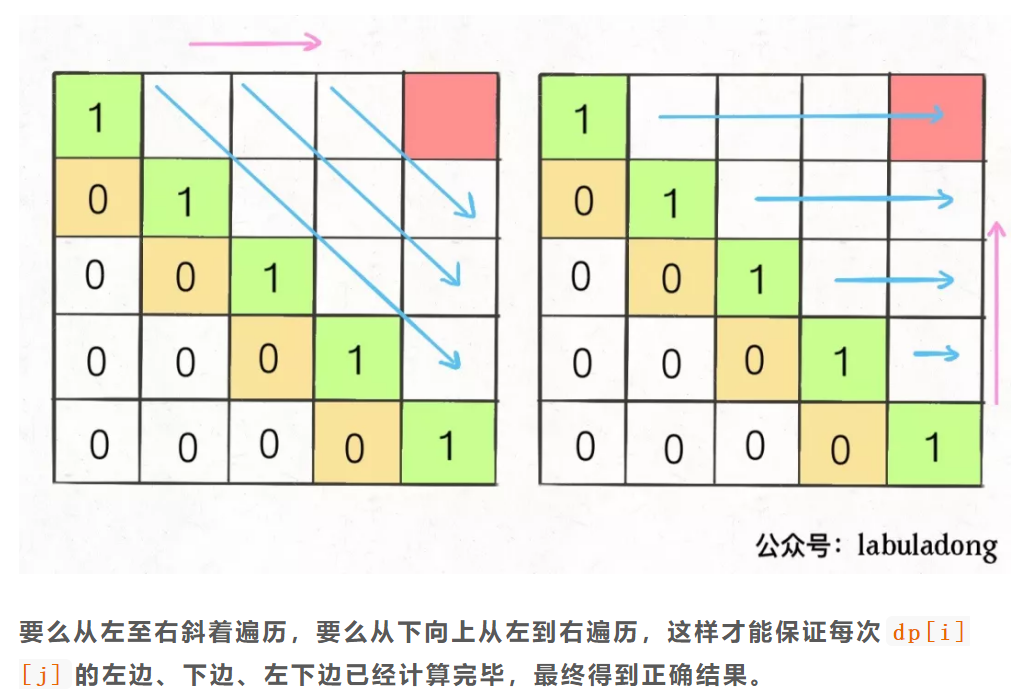
2、遍历的过程中,所需的状态必须是已经计算出来的。遍历的终点必须是存储结果的那个位置。主要就是看 base case 和最终结果的存储位置,保证遍历过程中使用的数据都是计算完毕的就行,




二、dp 数组的遍历方向

股票买卖 https://www.yuque.com/u1165446/ip7hhh/flp6xo
经典动态规划:编辑距离https://www.yuque.com/u1165446/ip7hhh/pybal9
经典动态规划:最长公共子序列



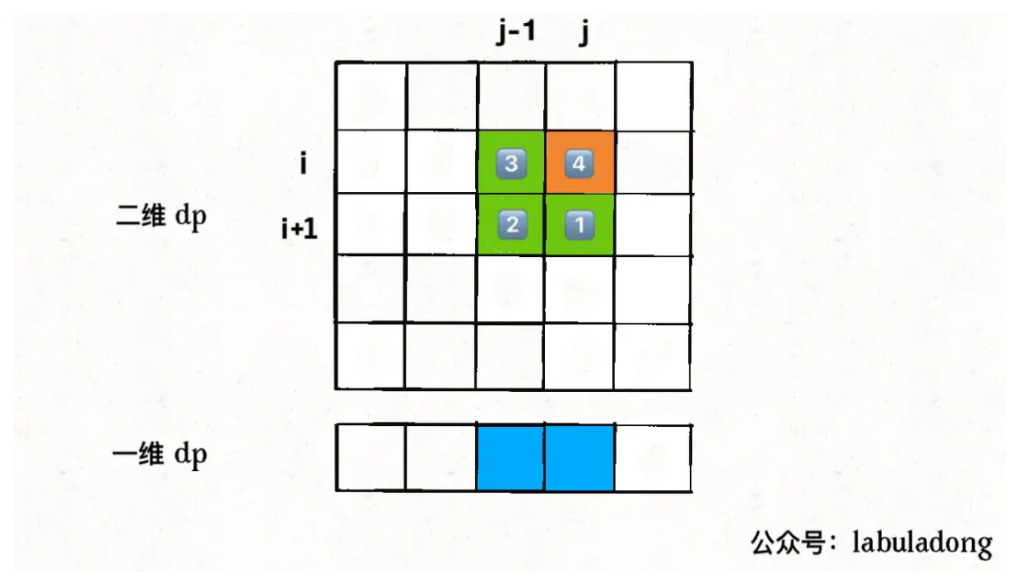
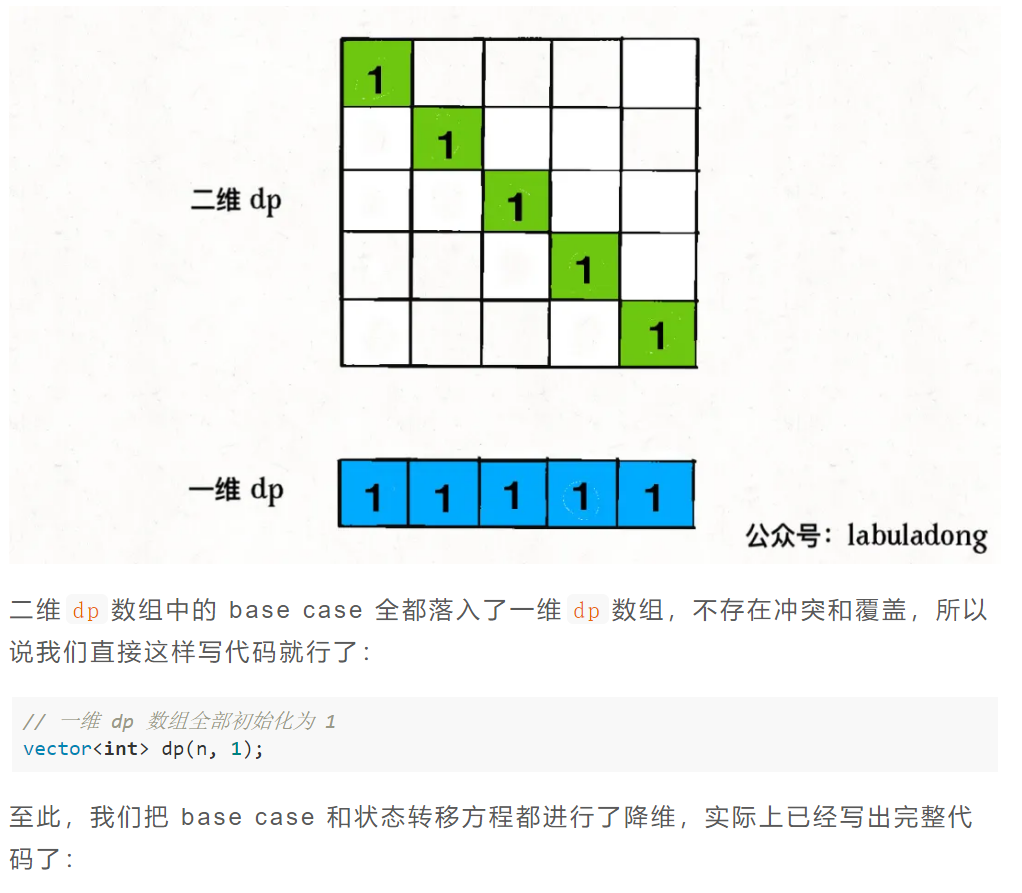
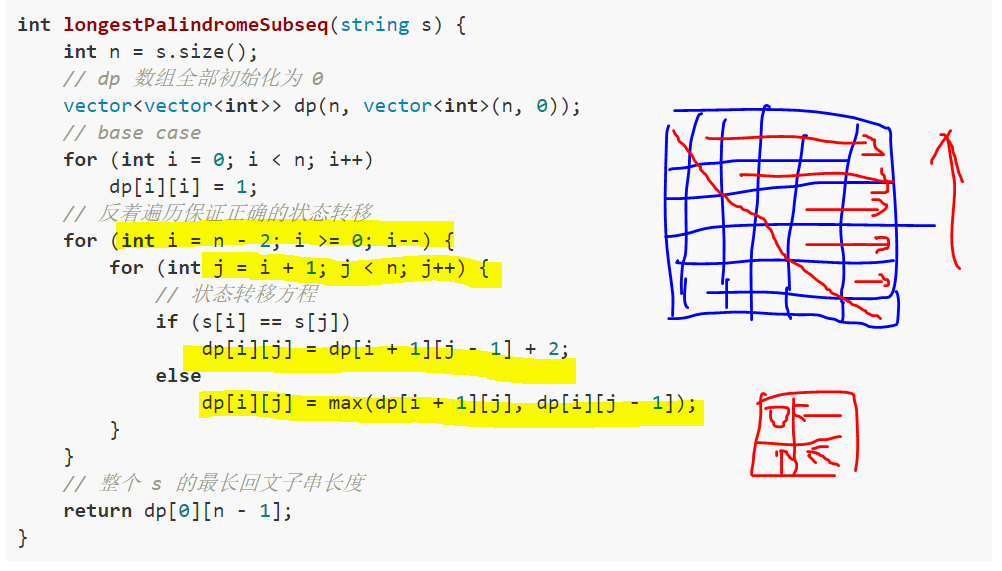
三、状态压缩


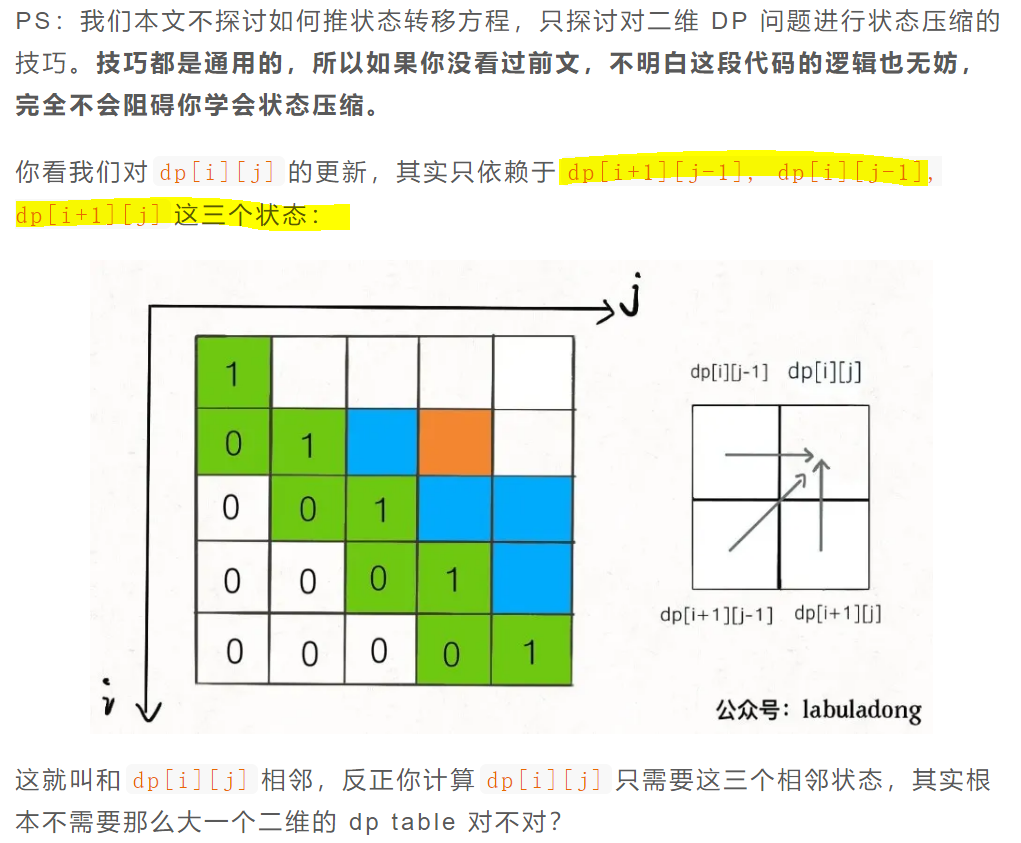
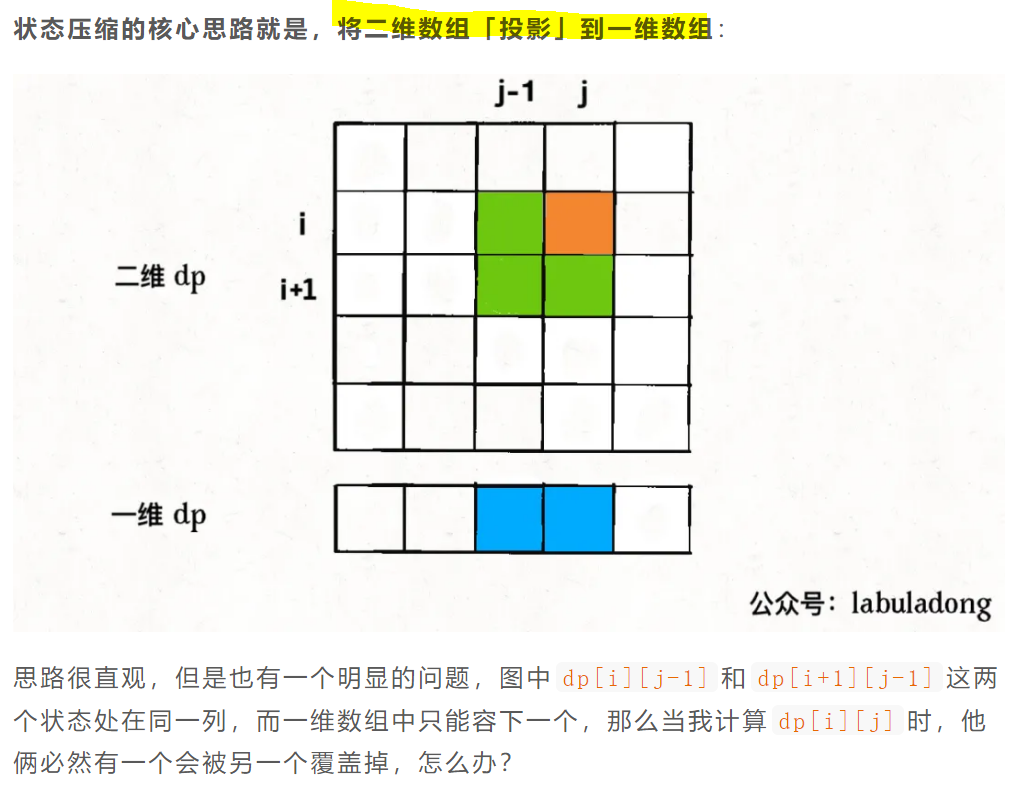


(绝了这里,我还傻乎乎的想D[J]是D[I][J],D[J+1]=D[I+1][J+1],换了之后,要根据新式子确定)