原作：

⼀、数据结构的存储⽅式

⼆、数据结构的基本操作

def traverse(arr):
    for i in range(len(arr)):

class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None
def traverse(self, head: ListNode):
    p = head
    while p:  # 迭代
        p = p.next
# 递归
 def traverse(self, head: ListNode):
    traverse(head.next)

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
# 递归
def traverse(self, root: TreeNode) :   
    traverse(root.left)
    traverse(root.right)

class TreeNode:
    def __init__(self, val=0, children=None):
        self.val = val
        self.children=TreeNode
def traverse(self,root:TreeNode):   # 瞎写的，不会
    for child in root.children:
        traverse(child)

三、算法刷题指南

def traverse(self, root: TreeNode) :   
    # 前序
    traverse(root.left)
    # 中序
    traverse(root.right)  
    # 后序

https://leetcode-cn.com/problems/binary-tree-maximum-path-sum/

class Solution:
    def maxPathSum(self, root: TreeNode) :
        self.maxsum = float('-inf')
        def dfs(root):
            if not root: return 0
            left = dfs(root.left)
            right = dfs(root.right)
            self.maxsum = max(self.maxsum, left + right + root.val)
            return max(0, max(left, right) + root.val)   # 神来之笔
        dfs(root)
        return self.maxsum

https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        if not preorder or not inorder:  # 递归终止条件
            return
        root = TreeNode(preorder[0])  # 先序为“根左右”，所以根据preorder可以确定root
        idx = inorder.index(preorder[0])  # 中序为“左根右”，根据root可以划分出左右子树
        # 下面递归对root的左右子树求解即可
        root.left = self.buildTree(preorder[1:1 + idx], inorder[:idx])
        root.right = self.buildTree(preorder[1 + idx:], inorder[idx + 1:])
        return root

https://leetcode-cn.com/problems/recover-binary-search-tree/

class Solution:
    def recoverTree(self, root: TreeNode) -> None:
        """
        Do not return anything, modify root in-place instead.
        """
        Trees = lambda x: [] if not x else Trees(x.left) + [x] + Trees(x.right)
        a = Trees(root)
        sa = sorted(a, key=lambda x: x.val)
        p, q = [a[i] for i in range(len(a)) if a[i] != sa[i]]
        p.val, q.val = q.val, p.val

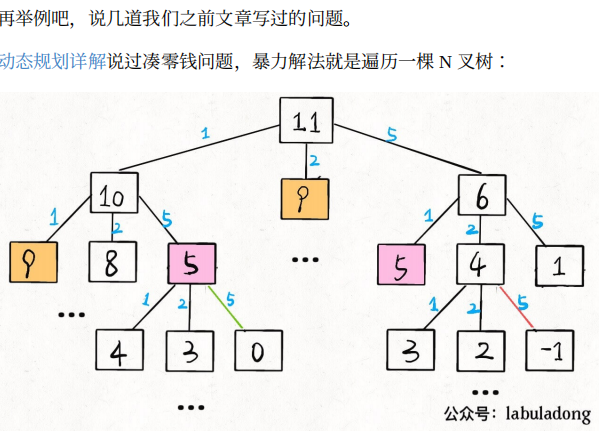
def coinChange(coins: List[int], amount: int): 
    def dp(n):   # 为组成金额 n 所需最少的硬币数量
        if n == 0: return 0 
        if n < 0: return -1 
        res = float('INF') 
        for coin in coins: 
            subproblem = dp(n - coin) 
            # ⼦问题⽆解，跳过 
            if subproblem == -1: continue 
            res = min(res, 1 + subproblem) 
        return res if res != float('INF') else -1
    return dp(amount)

# 不过是⼀个 N 叉树的遍历问题⽽已 
def dp(n): 
    for coin in coins: 
        dp(n - coin)

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        res = []
        s = "." * n
        def backtrack(i, tmp,col,z_diagonal,f_diagonal):
            if i == n:
                res.append(tmp)
                return 
            for j in range(n):
                if j not in col and i + j not in  z_diagonal and i - j not in f_diagonal:
                    backtrack(i+1,tmp + [s[:j] + "Q" + s[j+1:]], 
                              col | {j}, z_diagonal |{i + j} , f_diagonal |{i - j}  ) 
        backtrack(0,[],set(),set(),set())    
        return res