一、算法框架

queue = [起始点]    # 队列实现BFS
visited = set()    # 记录访问过的元素点，避免“回头”访问，陷入循环
visited.add(起始点)
step = 0
while queue:
    # 将所有节点同时向前扩散一步
    for _ in range(len(queue)):
        cur = queue.pop(0)
        if 找到目标:
            return 结果
        # 将cur的【所有相邻且没被访问过的节点】加入队列
        for near in cur的邻近节点：
            if near not in visited:
                queue.append(near)
                visited.add(near)
    step += 1    # 记录路径长度

def BFS(start, target):
    queue = collections.deque()     # 核心数据结构-队列
    visited = set()                 # 记录走过的路径，避免走回头路--使用集合，检索速度更快
    queue.append(start)    # 将起点加入队列
    visited.add(start)     
    step = 0                        # 记录扩散的步数
    while queue:
        size = len(queue)           
        for i in range(size):      # 将当前队列中的所有节点向四周扩散
            cur = queue.popleft()
            if cur == target:     # 判断是否到终点
                return step
            for node in cur:        # ？？？这里感觉代码不对，将cur的相邻节点加入队列
                if node not in visited:
                    queue.append(node)
                    visited.add(node)
        step += 1    # 更新步数
    return step

⼆、⼆叉树的最⼩⾼度

https://leetcode-cn.com/problems/minimum-depth-of-binary-tree/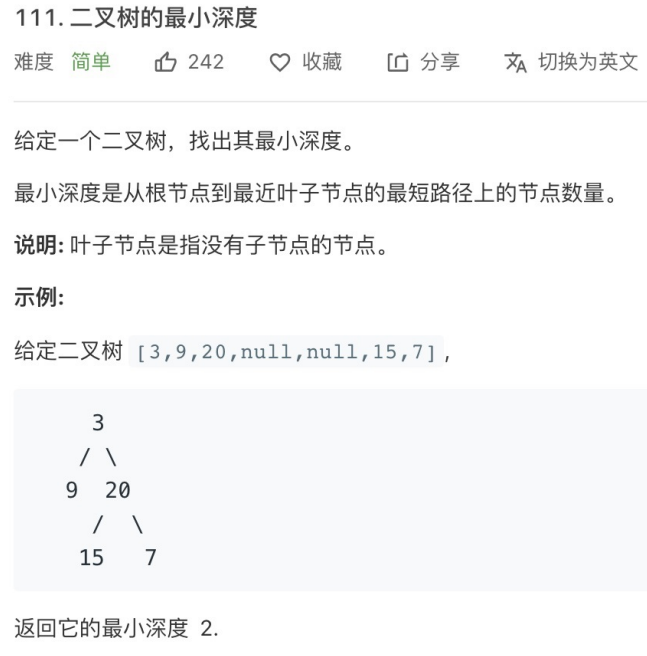

if not node.left and not node.right:

（下面的代码缺了扩散那一步，但是二叉树只有两个结点，同时按顺序出栈的，所以在循环过程中就已经扩散了）

class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        from collections import deque
        q = deque([(root, 1)])    # root本身是1层，初始化为1
        while q:
            node, depth = q.popleft()
            if not node.left and not node.right:
                return depth
            if node.left:
                q.append((node.left, depth + 1))
            if node.right:
                q.append((node.right, depth + 1))
        return 0

三、解开密码锁的最少次数

# 将 s[j] 向上拨动一次
def up(self, s:str, i:int) -> str:
        s_list = list(s)
        if s_list[i] == '9':
            s_list[i] = '0'
        else:
            s_list[i] = str(int(s_list[i]) + 1)
        return "".join(s_list)
# 将 s[i] 向下拨动一次
def down(self, s:str, i:int) -> str:
        s_list = list(s)
        if s_list[i] == '0':
            s_list[i] = '9'
        else:
            s_list[i] = str(int(s_list[i]) - 1)
        return "".join(s_list)
def openLock(self, deadends: List[str], target: str) -> int:
        # BFS
        queue = ['0000']
        visited = set()
        visited.add('0000')
        step = 0
        while queue:
            for _ in range(len(queue)):   # 向周围扩散
                cur = queue.pop(0) 
                #  判断是否到达终点
                for i in range(4):   # 将当前cur元素的所有邻近元素加入队列和visited
                    up = self.up(cur, i) 
                    queue.append(up)
                    visited.add(up)
                    down = self.down(cur, i)
                    queue.append(down)
                    visited.add(down)
            step += 1
        return -1

def openLock(self, deadends: List[str], target: str) -> int:
        # BFS
        queue = ['0000']
        visited = set()
        visited.add('0000')
        deadset = set(deadends)
        step = 0
        while queue:
            for _ in range(len(queue)):
                cur = queue.pop(0)
                if cur in deadset:
                    continue             # 如果cur是死亡数字，则不选这条路径
                if cur == target:
                    return step          # 如果cur = target，则找到目标，返回step
                # 将当前cur元素的所有邻近元素加入队列和visited
                for i in range(4):
                    up = self.up(cur, i)
                    if up not in visited:
                        queue.append(up)
                        visited.add(up)
                    down = self.down(cur, i)
                    if down not in visited:
                        queue.append(down)
                        visited.add(down)
            step += 1
        return -1

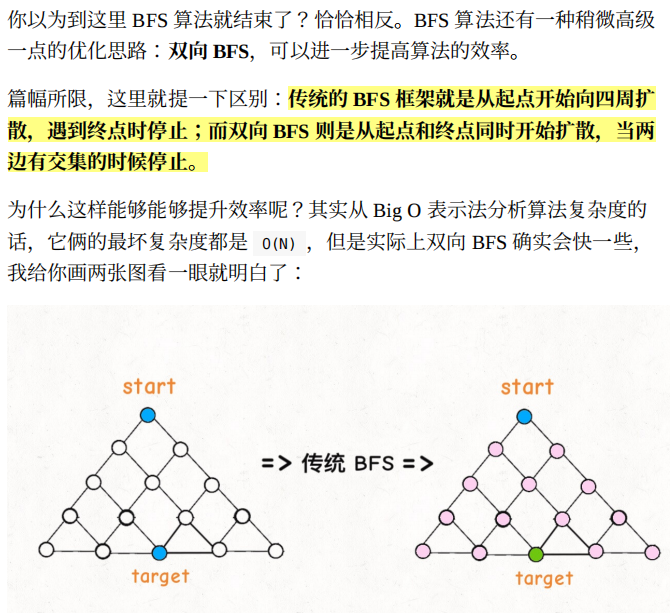
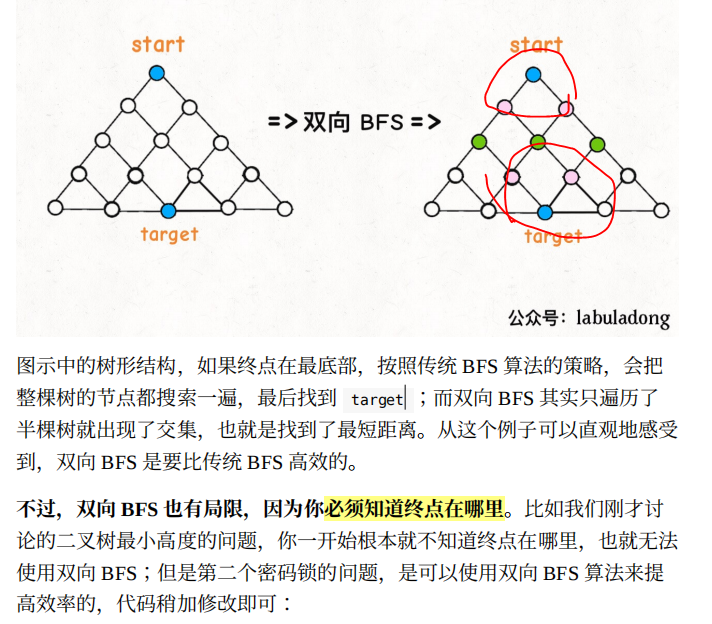
四、双向 BFS 优化

def openLock(self, deadends: List[str], target: str) -> int:
        # 双向BFS，用集合记录两边的扩散，set效率比list高，便于判断是否发生交集
        q1 = set()
        q1.add('0000')
        q2 = set()
        q2.add(target)
        visited = set()
        deadset = set(deadends)
        step = 0
        while q1 and q2:
            if len(q1) > len(q2):   # 选择⼀个较⼩的集合进⾏扩散，效率就会⾼⼀ 些
                q1, q2 = q2, q1
            temp = set()    # 记录扩散的结点
            for cur in q1:
                if cur in deadset:
                    continue
                if cur in q2:       # 如果两边扩散的元素出现交集，说明找到了最短路径
                    return step
                visited.add(cur)
                for i in range(4):
                    up = self.up(cur, i)
                    if up not in visited:
                        temp.add(up)
                    down = self.down(cur, i)
                    if down not in visited:
                        temp.add(down)
            step += 1
            # 交换q1和q2，q2存储着上一次q1扩散的结果temp
            q1 = q2
            q2 = temp       # q2始终记录上一次扩散时得到的元素
        return -1