二维DP

×10. 正则表达式匹配

class Solution:
    def isMatch(self, s: str, p: str) -> bool:
        m, n = len(s) + 1, len(p) + 1
        dp = [[False] * n for _ in range(m)]
        dp[0][0] = True
        # 初始化首行
        for j in range(2, n, 2):
            dp[0][j] = dp[0][j - 2] and p[j - 1] == '*'
        # 状态转移
        for i in range(1, m):
            for j in range(1, n):
                if p[j - 1] == '*':
                    if dp[i][j - 2]: dp[i][j] = True                              # 1.
                    elif dp[i - 1][j] and s[i - 1] == p[j - 2]: dp[i][j] = True   # 2.
                    elif dp[i - 1][j] and p[j - 2] == '.': dp[i][j] = True        # 3.
                else:
                    if dp[i - 1][j - 1] and s[i - 1] == p[j - 1]: dp[i][j] = True # 1.
                    elif dp[i - 1][j - 1] and p[j - 1] == '.': dp[i][j] = True    # 2.
        return dp[-1][-1]

×72. 编辑距离（困难）

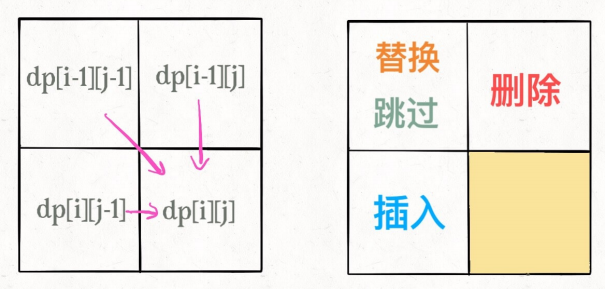
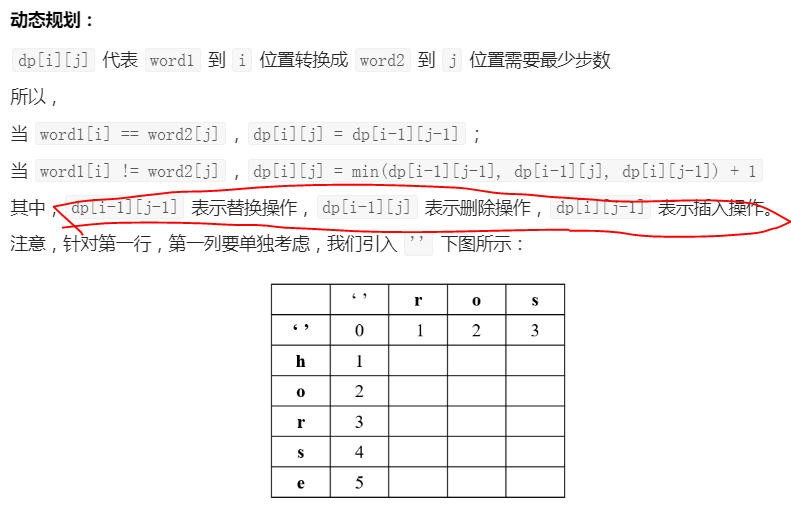
【i-1】【j-1】表示将word[i]替换成word[j]，删除表示删除word1[i-1]，插入表示在word1[j-1]前面插入

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        n1 = len(word1)
        n2 = len(word2)
        dp = [[0] * (n2 + 1) for _ in range(n1 + 1)] # 注意，行数为word1+1,列数为word2+1,dp[i][j]表示1到2的步数
        # 第一行，空字符到 word2
        for j in range(1, n2 + 1):
            dp[0][j] = dp[0][j-1] + 1
        # 第一列，word1 到空字符串
        for i in range(1, n1 + 1):
            dp[i][0] = dp[i-1][0] + 1
        for i in range(1, n1 + 1):  # 注意索引值
            for j in range(1, n2 + 1):
                if word1[i-1] == word2[j-1]:
                    dp[i][j] = dp[i-1][j-1]
                else:
                    dp[i][j] = min(dp[i][j-1], dp[i-1][j], dp[i-1][j-1] ) + 1
        #print(dp)      
        return dp[-1][-1]