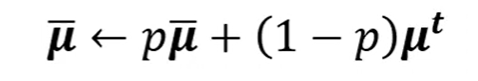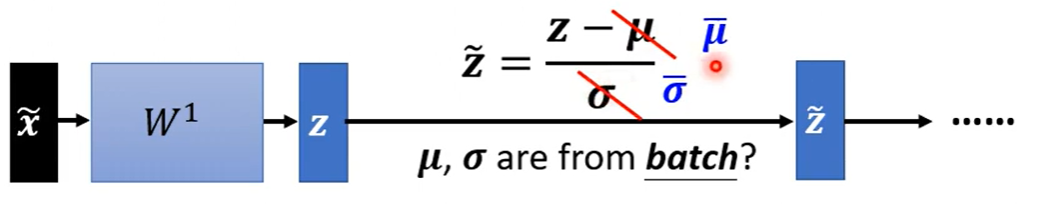1. 局部最小值（local minima）与鞍点（saddle point）

1.1 如何判断local minima & local maxima & saddle point

Gradient（梯度）和hessian（黑塞矩阵）的计算方法：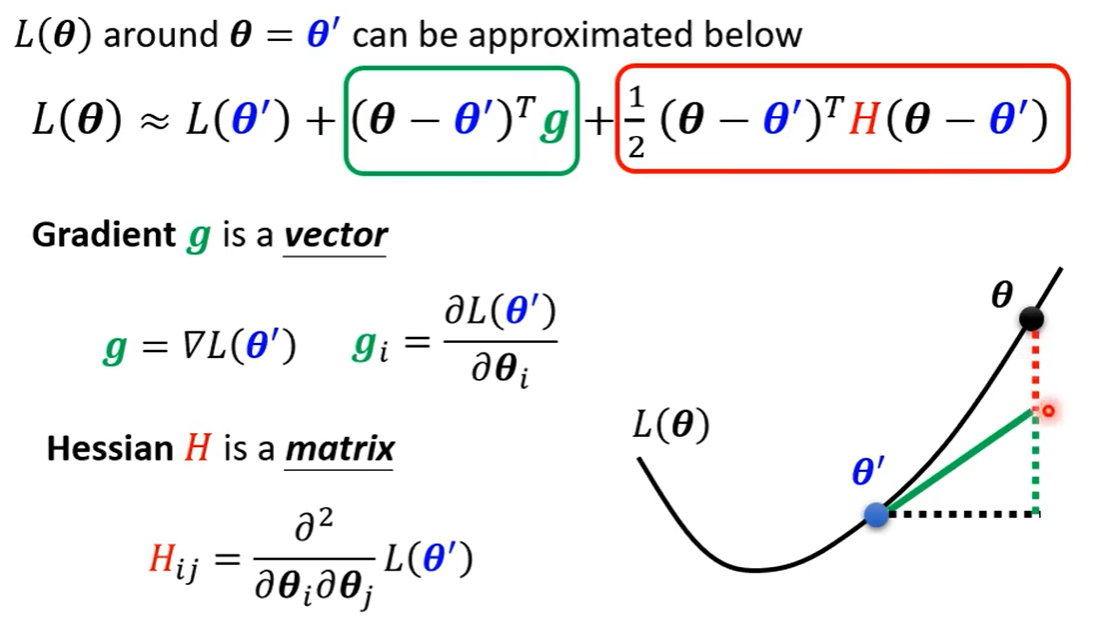
image.png
训练不起来 -> 遇到了critical point（驻点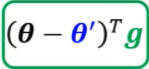）-> image.png 为0
因此只需要看 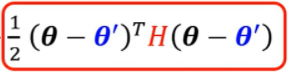image.png 的正负

  • H的特征值均为正数：Local minima
  • H的特征值均为负数：Local maxima
  • H的特征值有正有负：Saddle point

    1.2 local minima & saddle point 哪种情况更常见

    多数情况下，实验中都不会达到一个真实的local minima，而是卡在了saddle point

2. 批次（batch）与动量（momentum）

2.1 Small Batch & Large Batch

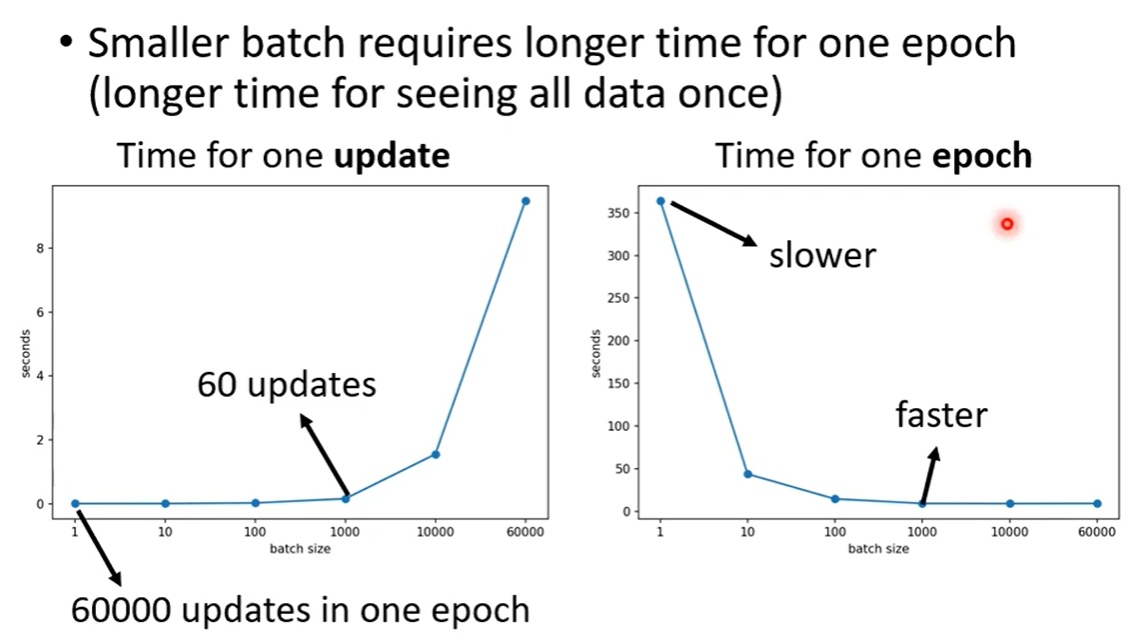
image.png
有些情况下，Small Batch表现更好，原因是如果遇到Saddle Point，Full Batch无法继续训练，而Small Batch可以换下一个Batch来继续计算Loss.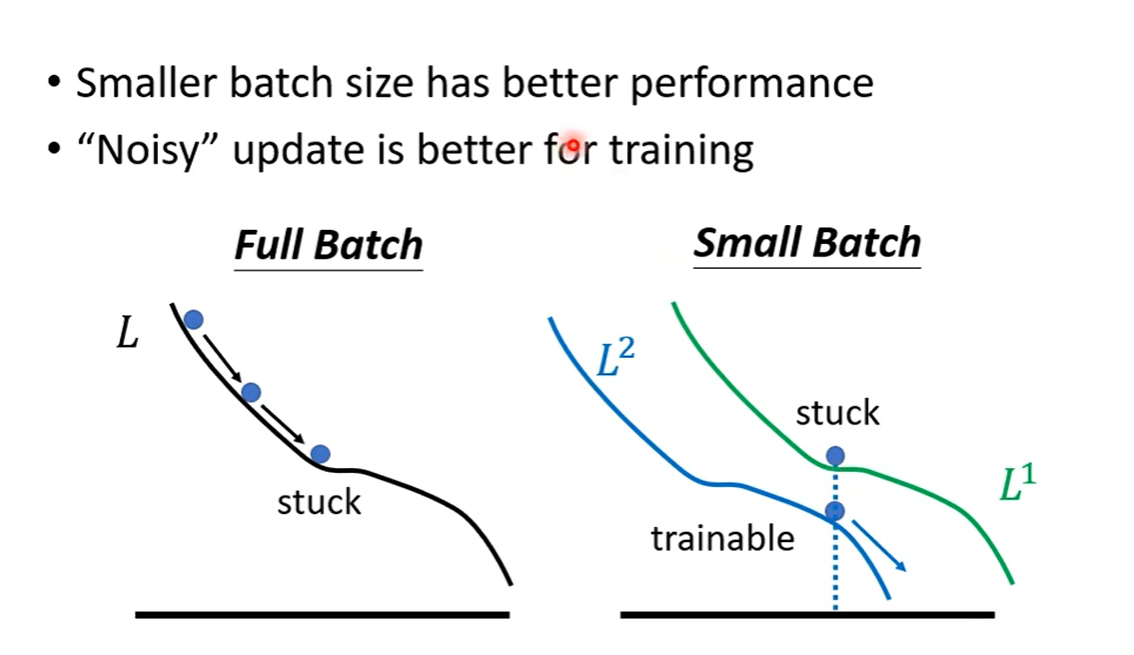image.png
Batch size也是需要调的超参数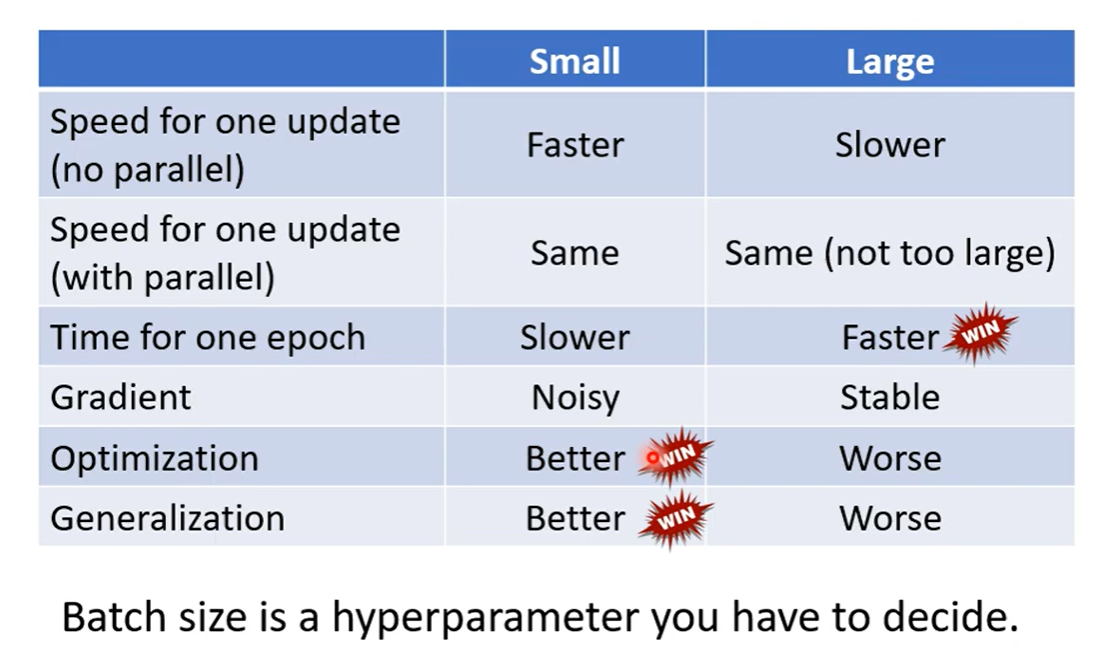
image.png
下一次update的方向由Gradient和Momentum（上一步的方向）共同决定，可以逃离Local minima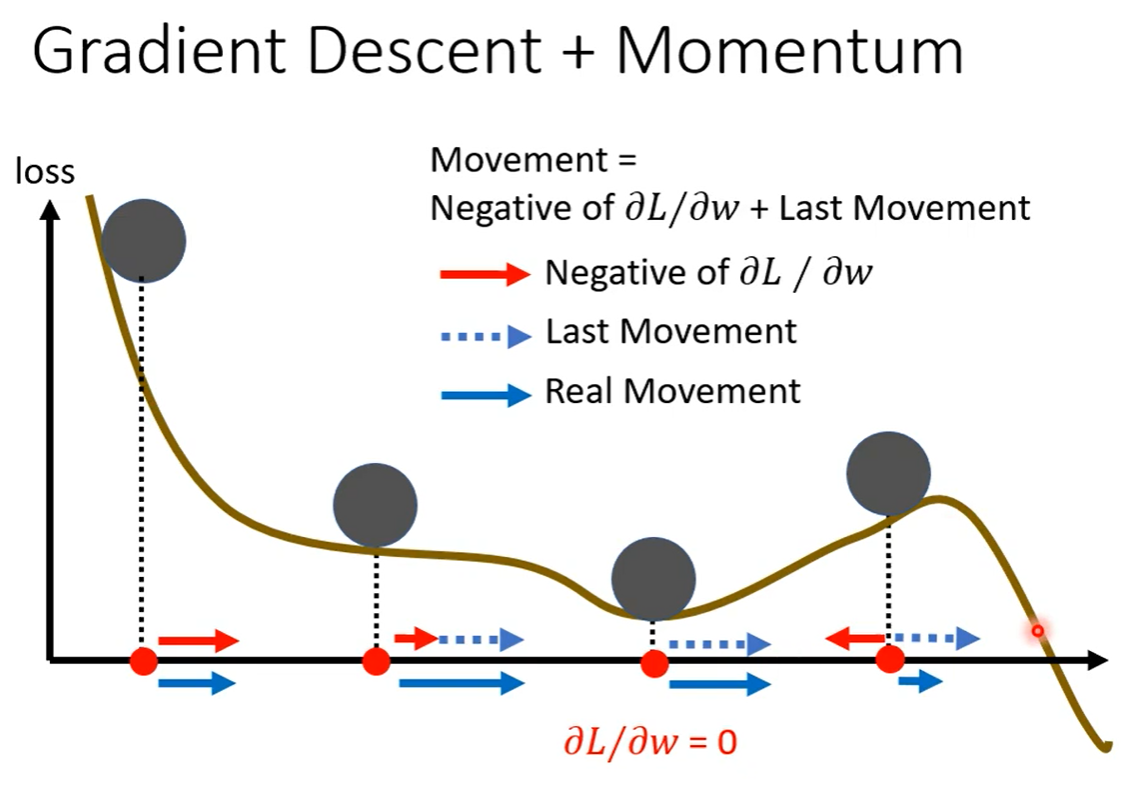
image.png

3. 自动调整学习速率（Learning Rate）

Learning Rate采用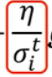image.png，来update参数
gradient小的时候，Learning Rate大
gradient大的时候，Learning Rate小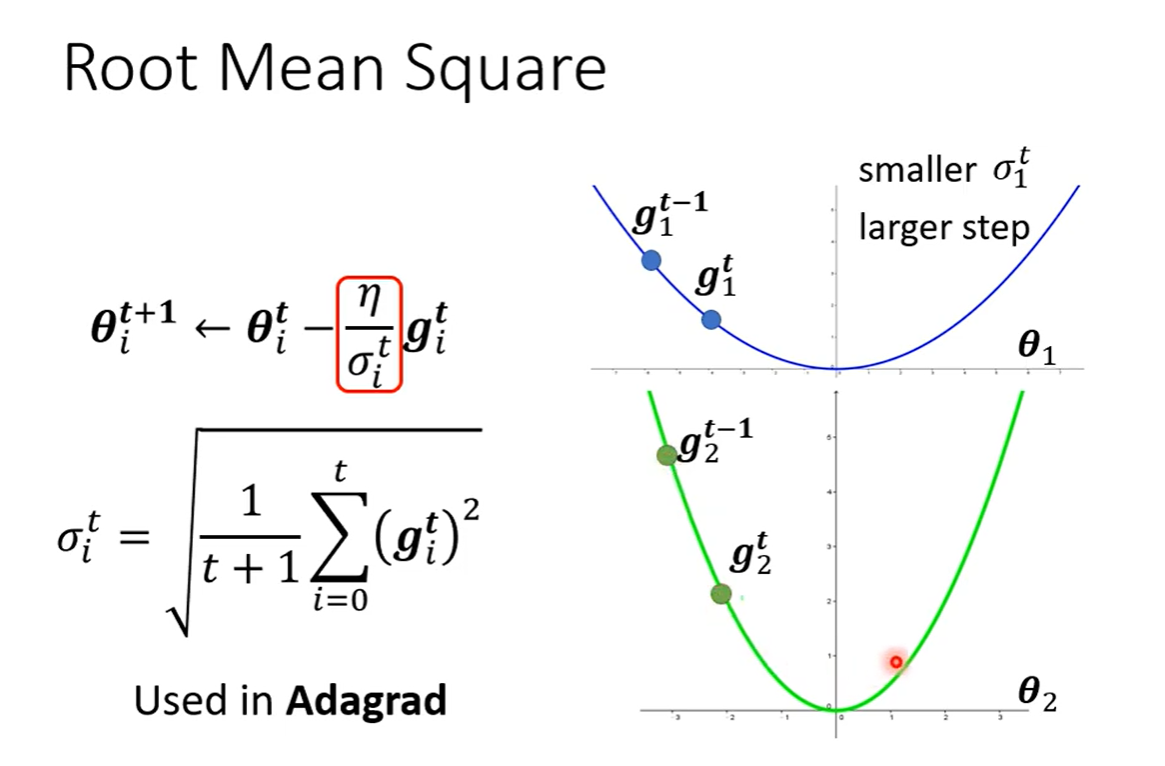
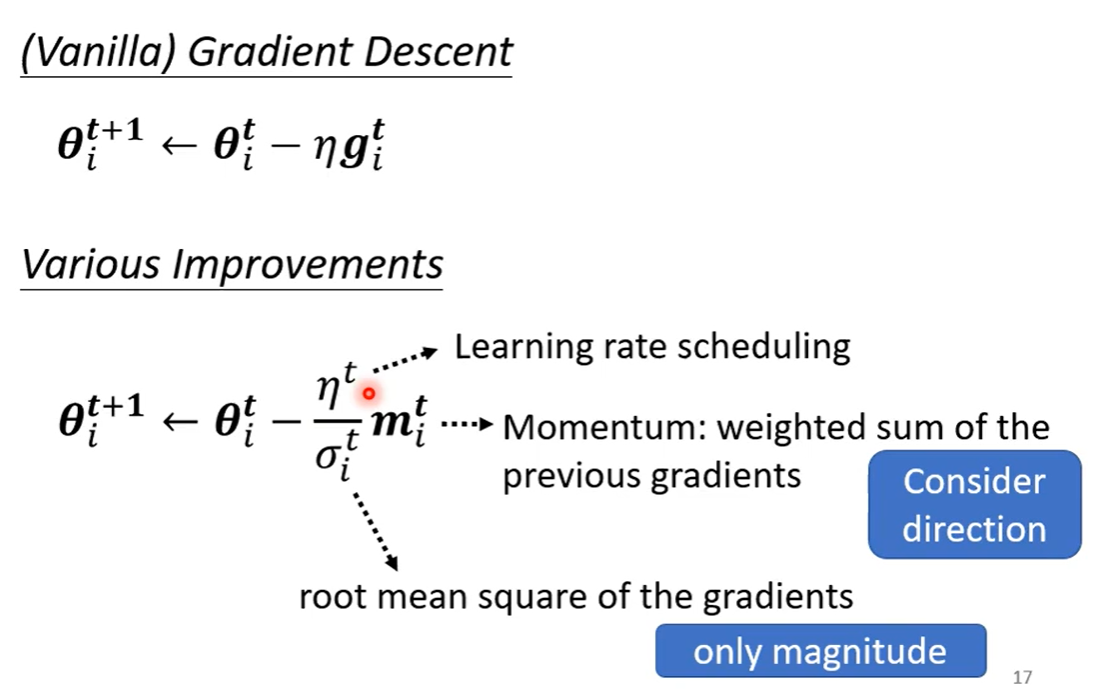
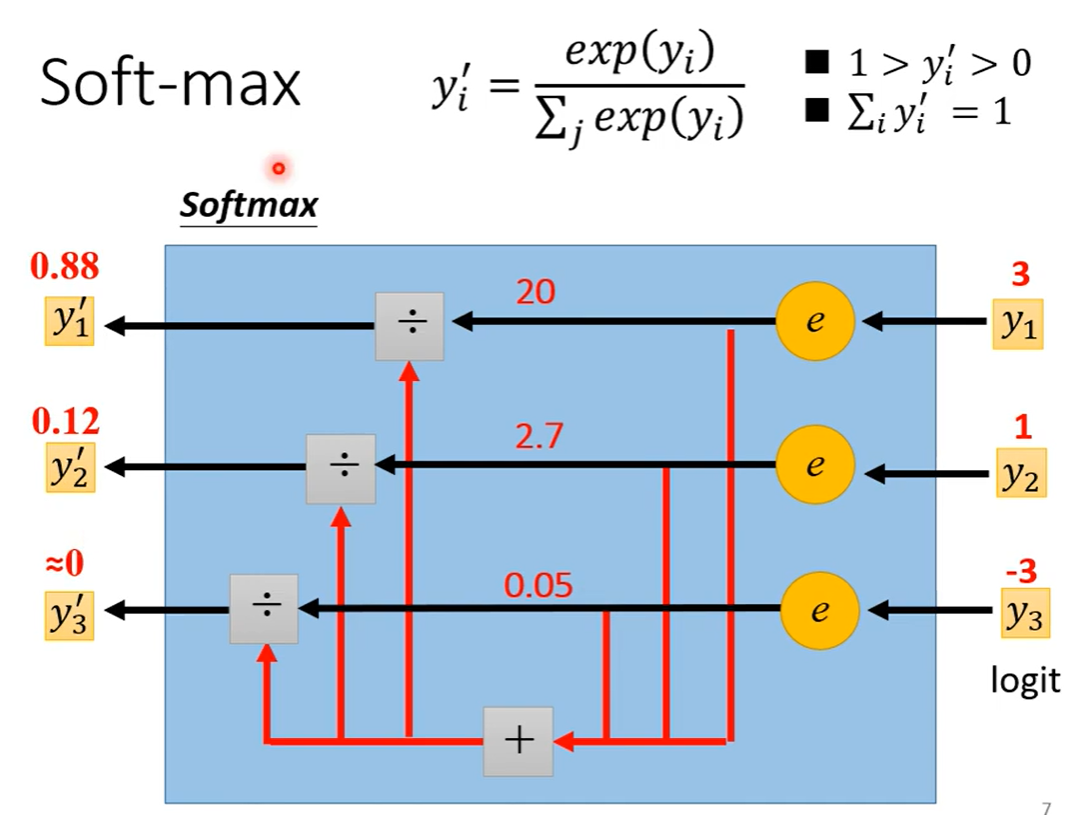
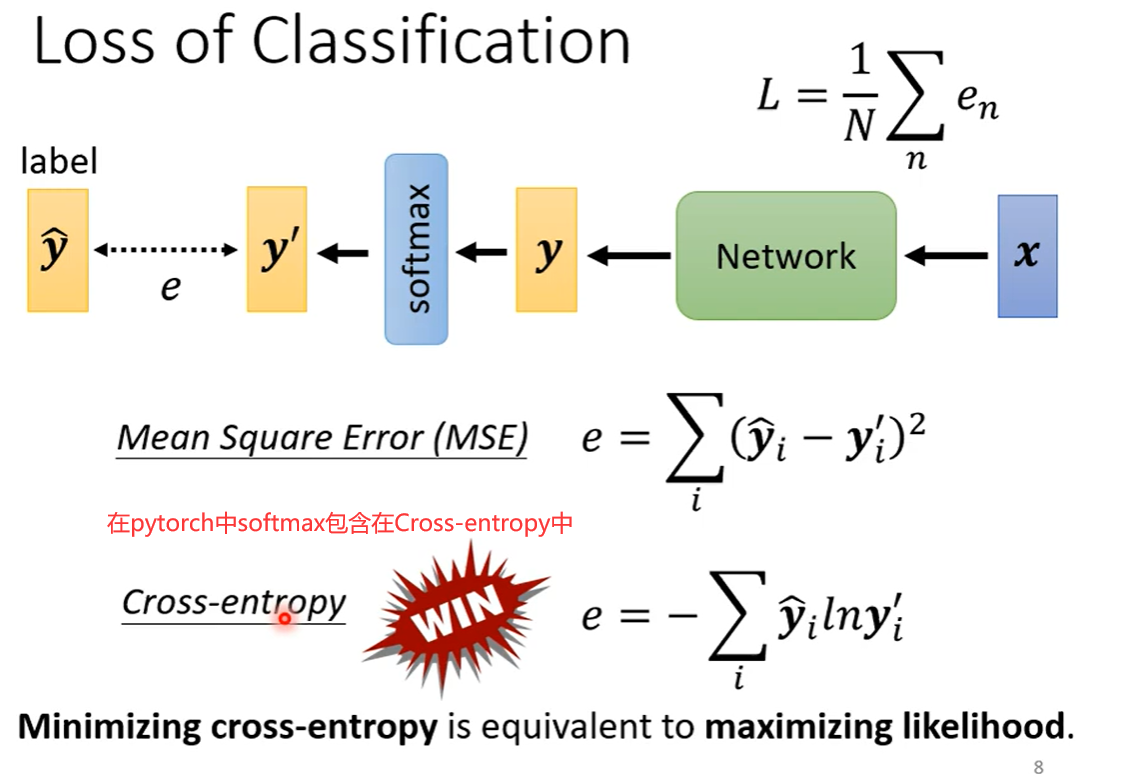
image.png
image.png

4. 损失函数（Loss）也可能有影响

softmax函数：把参数值移到0~1之间
image.png
image.png

5. 批次标准化（Batch Normalization）

Batch Normalization，批次标准化，和普通的数据标准化类似，是将分散的数据统一的一种做法，也是优化神经网络的一种方法。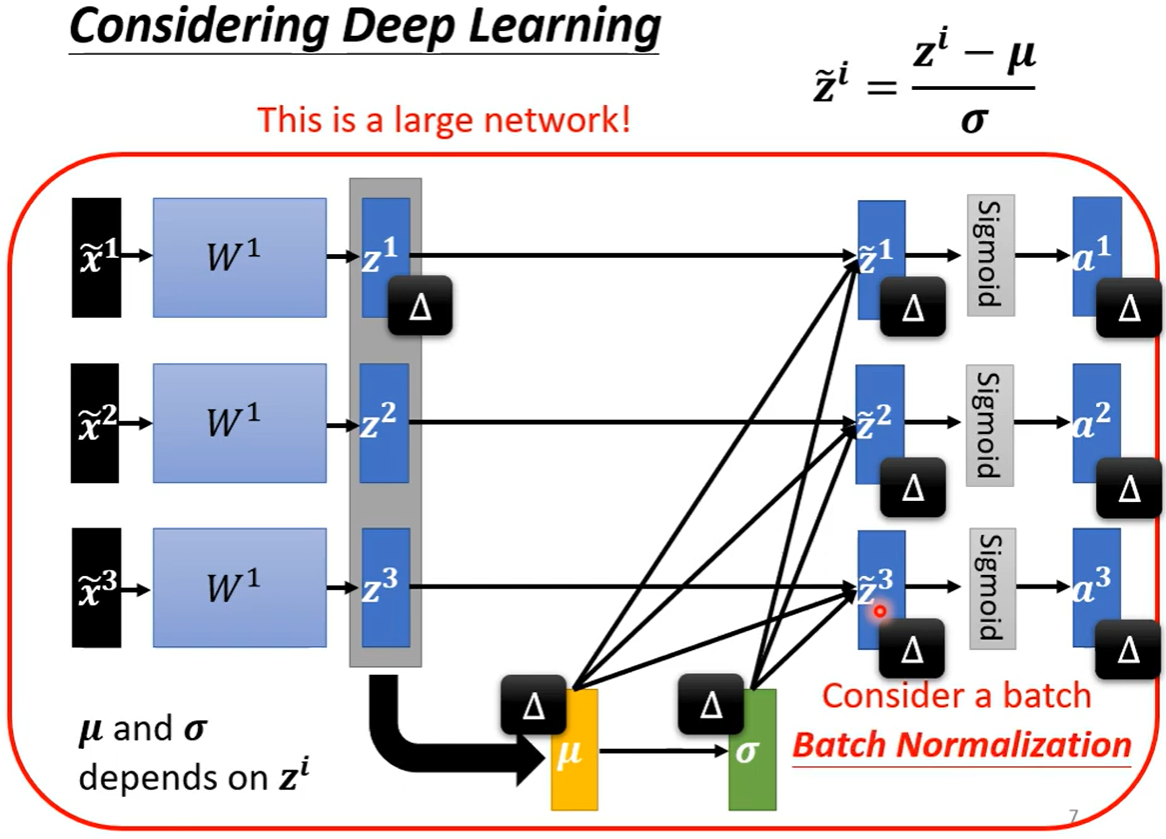
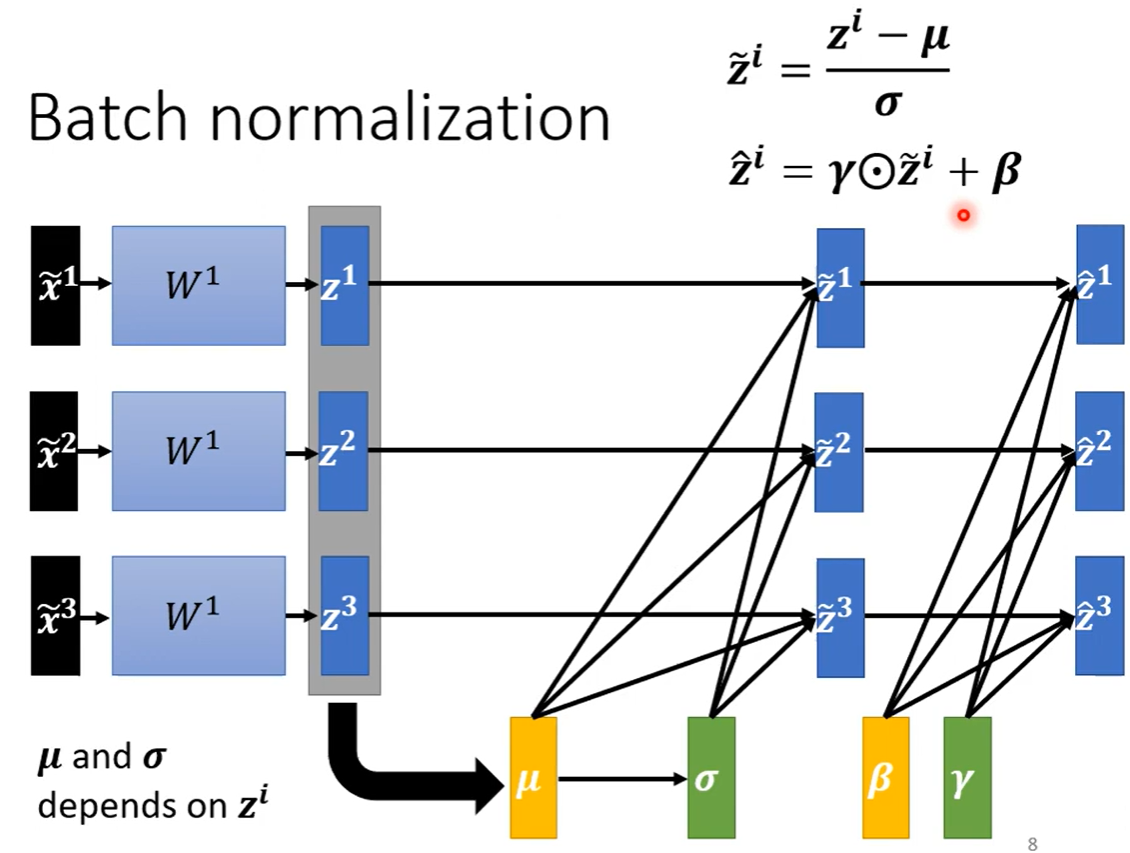
image.png
image.png
Training的时候，每次取一个batch出来的时候就算出一个μ和σ
Testing的时候只需要代入μ和σ的平均值
image.png
image.png