图解
文档
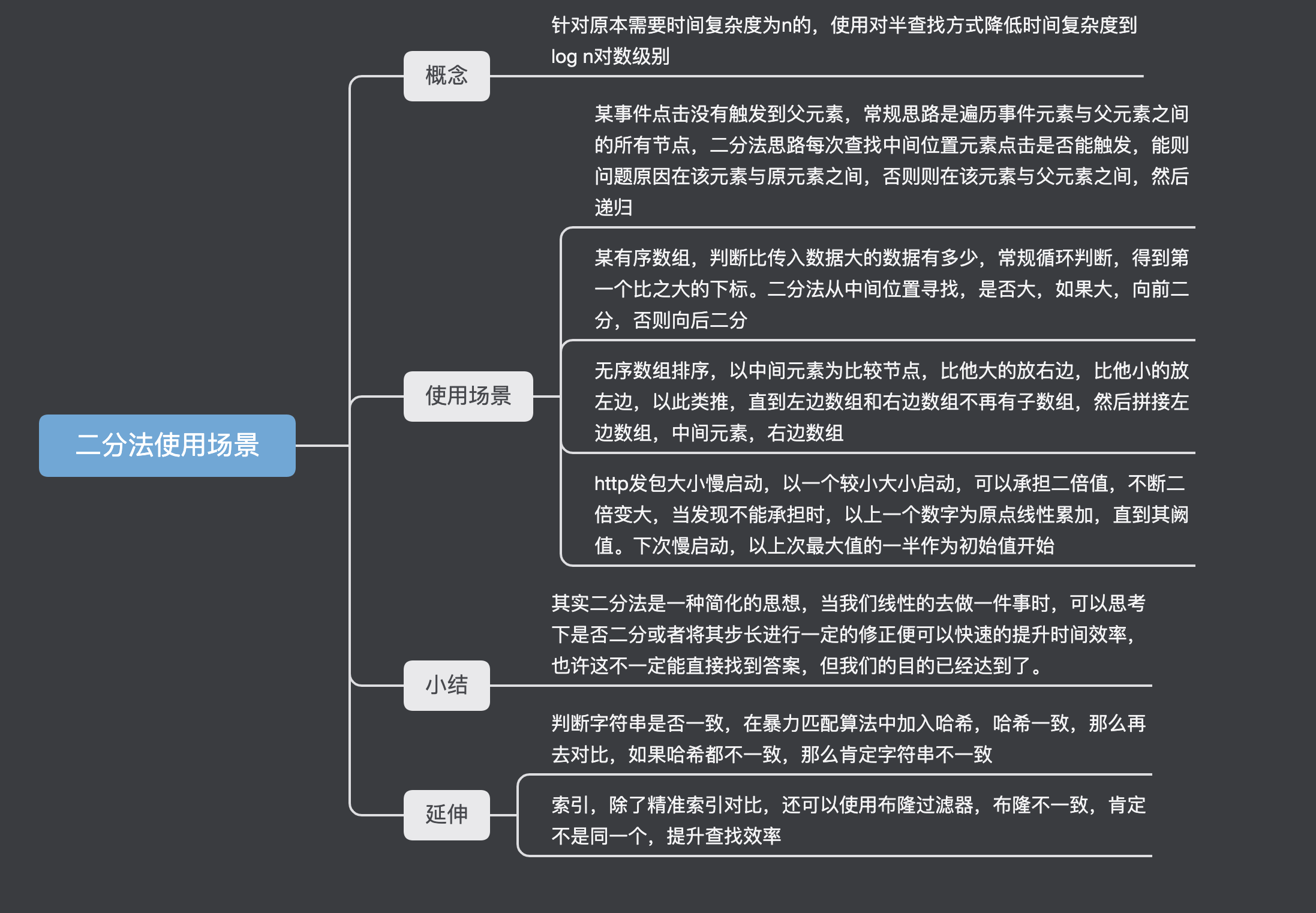
概念
- 针对原本需要时间复杂度为n的,使用对半查找方式降低时间复杂度到log n对数级别
使用场景
某事件点击没有触发到父元素,常规思路是遍历事件元素与父元素之间的所有节点,二分法思路每次查找中间位置元素点击是否能触发,能则问题原因在该元素与原元素之间,否则则在该元素与父元素之间,然后递归
某有序数组,判断比传入数据大的数据有多少,常规循环判断,得到第一个比之大的下标。二分法从中间位置寻找,是否大,如果大,向前二分,否则向后二分
无序数组排序,以中间元素为比较节点,比他大的放右边,比他小的放左边,以此类推,直到左边数组和右边数组不再有子数组,然后拼接左边数组,中间元素,右边数组
http发包大小慢启动,以一个较小大小启动,可以承担二倍值,不断二倍变大,当发现不能承担时,以上一个数字为原点线性累加,直到其阙值。下次慢启动,以上次最大值的一半作为初始值开始
小结
- 其实二分法是一种简化的思想,当我们线性的去做一件事时,可以思考下是否二分或者将其步长进行一定的修正便可以快速的提升时间效率,也许这不一定能直接找到答案,但我们的目的已经达到了。
延伸
判断字符串是否一致,在暴力匹配算法中加入哈希,哈希一致,那么再去对比,如果哈希都不一致,那么肯定字符串不一致
索引,除了精准索引对比,还可以使用布隆过滤器,布隆不一致,肯定不是同一个,提升查找效率

