前言

rk算法是bf算法的进化版本，

理论解释

rk算法主要是优化主串的子串与模式串的比对，原来的对比时间复杂度为m，经过优化之后整体的时间复杂度变为O(n).

简化子串与模式串的比较

为了简化比较的逻辑，我们将字符串的使用范围变为字母a-z。

哈希值比较

于是，我们按照26进制去考虑，然后将每个串可以变为一个哈希值。但是这样存在一个问题，就是相加得到的哈希值很容易导致冲突。

解决哈希冲突的有效方式，将原来的自然数变为素数，这样就大程度的降低了重复的概率。

  1. const hashFn = (str)=>{
  2.   let strArr = str.split(''),hash=0,hashDict={
  3.     'a':1,
  4.     'b':2,
  5.     'c':3,
  6.     'd':5,
  7.     'e':7,
  9.   }
  10.   strArr.forEach(function(s,index){
  11.     hash += hashDict[s] * Math.pow(26,index)
  12.   })
  13.   return hash
  14. }
  16. // 原来的循环比较算法变为
  17.  if(hashFn(target.substring(i,i+m))===hashFn(pattern)){
  18.       return true
  19.   }

如果担心素数得到的哈希仍有冲突，可以补充进进一步直接比较字符串的方式

if(hashFn(target.substring(i,i+m))===hashFn(pattern) && target.substring(i,i+m)===pattern){ return true }

当然你也可以优化hashFn，如果发现这个hash值已经存在 那么返回的哈希值在进行额外的加值，降低哈希冲突的可能。

缓存发现具有规律的子串

在对比中我们发现当从第一个子串到第二个子串进行哈希计算的时候，发现其中具有m-1个字符串是相同的，并且每两个相邻的都具有如此的特征。

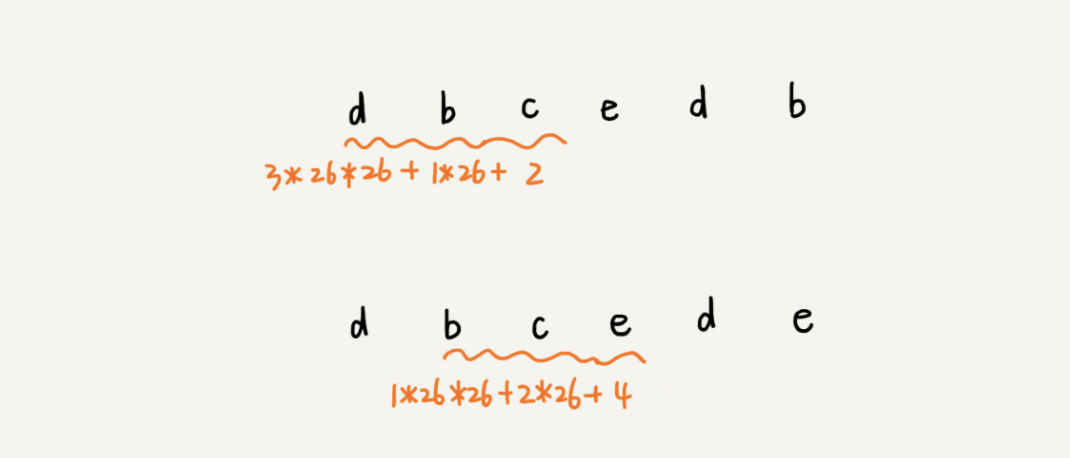
image.png

也就是h(i) 与 h(i-1)中间部分的字符串具有相同的结果，减去其第一个值,剩下的值乘26可以得到后续的值，再加上其最后的值就是h(i)的值。

另外在哈希的计算中，发现从26,一直到26^m,为了避免在每次hash值中重复计算，我们预先将其计算好，缓存起来，供查询使用，可以大幅度提高运行的效率。

代码实现

代码地址： https://codepen.io/robinson90/pen/eYORqGV