递归

题目：台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

找到中止条件，然后判断假定是最后一步是定死的，就是一步或者两步，然后等于前面所有方法数之和即可。

即使前面的跳法有很多相同的，只要最后一步是不同的，那么就是不同的

代码

function jumpFloor(number)
{
    if(number>3){
        return jumpFloor(number-1) + jumpFloor(number-2)
    }else {
        return number
    }
}

升级版

这次可以跳1-n级台阶，有多少中跳法 ？

代码

思路类似，只是中止条件不同了。另外可以发现，实际每次台阶都是两次选择，可以选择直接跳，也可以选择忽略这个台阶。

function jumpFloorII(number)
{
    let sum = 0 
    if(number>2){
        return 2*jumpFloorII(number-1)
    }else {
       return number 
    }
}

function jumpFloorII(number)
{
       return Math.pow(2,number-1) 
}

矩形拼接

我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。请问用n个21的小矩形无重叠地覆盖一个2n的大矩形，总共有多少种方法？比如n=3时，23的矩形块有3种覆盖方法：

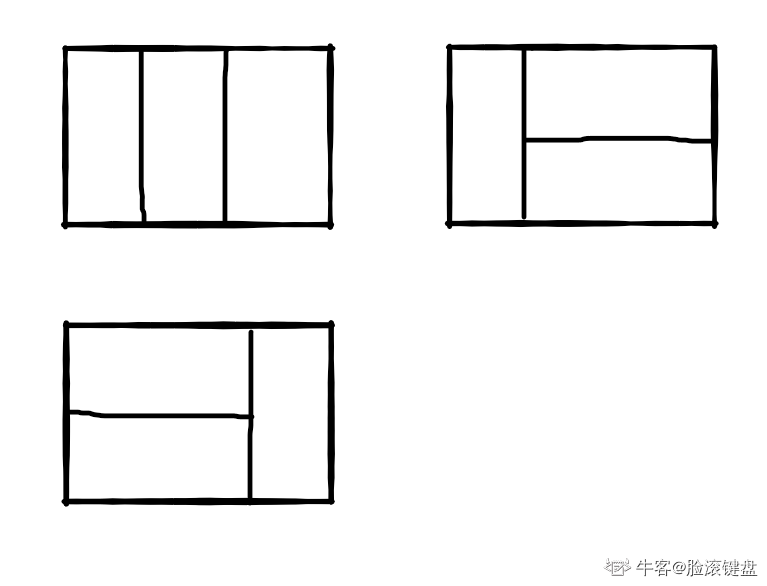
function rectCover(number)
{
    if(number<=2){
        return number
    }else {
       return  rectCover(number-2)+ rectCover(number-1)
    }
}

当然也可以从前面的算法累加到当前，更节省内存。

function rectCover(number)
{
    if(number<=2){
        return number
    }else {
        let prev = 2,prev_2 = 1,temp=0
        for(let i =2;i<number;i++){
            temp = prev + prev_2
            prev_2 = prev
            prev = temp 
        }
        return temp 
    }
}