1. 超越经典概述
1.1 超越经典搜索
- 单一类别的问题,其解决方案是具有如下特点的一系列动作
- 可观测(observable)
- 确定性(deterministic)
- 已知环境( known environment)
本章我们将讨论
搜索算法被设成系统地探索问题的空间。
- 该系统性是由以下方法得到的
在内存中保持一条或多条路径,并且在沿着该路径的每个点上记录哪些已被探索过。
- 目标被找到时,该路径也就构成问题的一个解。然而,在许多问题中,到达目标的路径是无关紧要的。
局部搜索算法和最优化问题例子:n-皇后向题
在 nxn 棋盘上摆放n个皇后,使得任意两个皇后互相都攻击不到
我们关心最后的棋局,而不是皇后加入的先后次序。
1.3 局部搜索
局部搜索是一种不同类型的算法,具有如下特点
- 它不介意什么路径
- 局部搜索算法使用一个当前节点(而不是多条路径),并且通常仅移动到该节点相邻的节点通常,搜索后不保留该路径。
优点
在很多的最优化问题中,不需要知道到达目标的路径,目标状态本身才是问题的解。
- 除了寻找目标之外,局部搜索算法对解决纯优化问题也很有效。
- 优化的目的是根据—个目标函数找到其最好的状态。
- 但是许多优化问题并不适合采用前面介绍的搜索算法。
例如,达尔文进化论可以被看作是试图优化,但对于这—问题,即没有“目标测试"、也没有“路径代价”。
(将「适者生存」作为自然界的优化函数。当然这个问题不好做「目标测试」和计算「路径耗散」)
- 对于这类问题,可以采用局部搜索算法,通过不断改进当前状态,直到它满足约束为止。
许多应用问题是与路径无关的,目标状态本身就是解。例如:
是一个沿着值增加的方向持续移动的简单循环过程
- 当到达一个山峰时就停止。
- 爬山法不根据当前状态考虑计划未来后继节点。就像雾中登山一样。
- 当有多个继节点时,爬山法选取最优后继节点集中的一个。
特点
大多数基本的局部搜索算法都不保持一棵搜索树。
最陡爬坡版( Steepest-ascent version )
当前节点每一步都用最佳邻接点(具有最高值的邻接点)替换,否则到达一个"峰值’
优缺点
- 爬山搜索算法是最基本的局部搜索方法。
- 它常常会朝着一个解快速地进展,因为通常很容易改善—个不良状态。
- 爬山法也往往被称为局部贪婪搜索, 因为它只顾寻找一个好的邻接点的状态,而不提前思考下一步该去哪儿。
- 尽管贪婪被认为是“七宗罪”之一,但是贪婪算法往往表现的相当好。
爬山搜索: 8皇后问题
- 问题形式化: 完全状态形式化。
- 后继函数: 移动—个皇后到同列另—个方格中的所有可能状态。
7*8=56个后继状态
- 启发函数: 可以互相攻击的皇后对数(直接或间接)。该函数的全局最小值是0.
h =互相攻击到的皇后对数
如图这个状态: h =17
- 一个局部最小值点(h = 1)
依照爬山法该问题求解以失败结束
统计结果:8皇后问题86%都会卡住,但算法速度很快成功的最优解平均步数是4。被卡住的平均步数是3
几个概念:目标函数、全局最优、局部最优、山肩、平原…
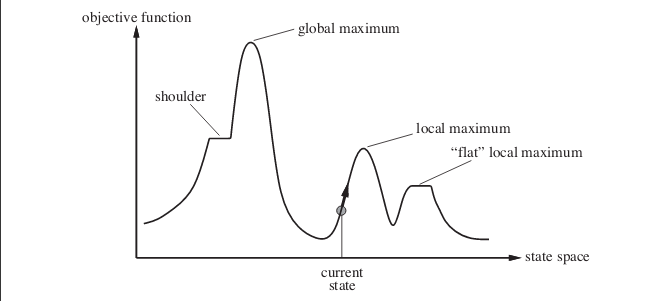
- 依赖千初始状态,容易陷千局部最优。
爬山法的弱点
如下三种情况经常被困:
- 局部极大值(Local maxima)
高于相邻节点但低于全局最大值。
- 高原(Plateaux) :
平坦的局部最大值,或山肩。即—块状态空间区域的评价函数值是相同的。
- 山脊(Ridges):
—系列连续的局部极大值,对于贪婪算法去引导的搜索是困难的。
爬山法变种(Variants of Hill Climbing) :
随机爬山法
以上二种:试着避开局部最大。
随机重启开始爬山法
随机生成的初始状态直到找到目标。它十分完备,重新开始
这个算法完备率接近1 。
侧向移动:采用限制次数的方法限制侧移次数,避免死循环。
改进后的8皇后问题,侧移设置为100次成功率由14%上升到94% 。
2.2 局部束搜索(Local Beam Search)
内存中仅保存一个节点似乎是对内存限制问题的极端反应。
局部束搜索: 保存k状态,而不是一个状态
- 从K 个随机产生的状态开始
- 每次迭代,产生K 个状态的所有后续
- 如果任何一个新产生的状态是目标状态,则停止。否则从所有后续中选择 k 个最好的后续,重复迭代。
//同随机重新开始的区别:在K条线程中共享信息。
- 缺点: 局部束搜索会很快地集中在状态空间的某个小区域内,使得搜索代价比爬山要昂贵。缺乏多样性。
改进的随机变种:它不是选择k个最佳后继节点,而是以选择后继节点的概率是其值的递增函数,来随机地选择k个后继节点。(随机束搜索有些类似于自然选择的过程)
2.3 禁忌搜索(Tahu Search)
基本思想
禁忌(prohibited or restricted by social custom),指的是不能触及的事物。
禁忌搜索是由弗雷德·格洛弗于1986年提出,1989年加以形式化。
- 它是一种元启发式算法,用于解决组合优化问题。
- 它使用一种局部搜索或邻域搜索过程,从一个潜在的解x到改进的相邻解x’ 之间反复移动,直到满足某些停止条件。
-
禁忌搜索的三种策略
禁止策略:控制何物进入该禁忌表。
- 释放策略:控制何物以及何时退出该禁忌表。
- 短期策略:管理禁止策略和释放策略之间的相互作用来选择试验解。
特赦策略:禁忌搜索算法中,迭代的某一步会出现候选集的某一个元素被禁止搜索,但是若禁该元素,则会使评价函数有所改善,因此我们需要设置一个特赦规则,当满足该时该条时该元素从禁忌表中跳出。
可用禁忌搜索解决的问题
旅行推销员问题
- 旅行比赛问题
- 车间作业调度问题
- 网络加载问题
- 图着色问题
- 硬件/软件划分
- 最小生成树 问题
最小生成树问题(Minimum Spanning Tree Problem
目标:用最小代价连接所有节点
约束1:仅当包含连接DE时,才可以包含连接AD。(处罚:100)
约束2:至多可以包含三个连接(AD,CD和AB)中的一个。
(处罚:若选择了三个中的两个则处罚100,选择了全部三个则罚200)
步骤略(P25
禁忌搜索的应用领域
- 资源规划通讯
- 设计
- 金融分析
- 调度
- 空间规划
- 能源分配
- 分子工程
- 后勤保障
- 柔性生产
- 废物管理
- 矿产勘探
- 生物医药分析
-
3. 优化算法
3.1 模拟退火 Simulated Annealing
基本思想
引论:爬山法从不下山的策略导致其不完备性,而纯粹的随机行走,又导致效率的低下,把单纯的爬山法和纯粹的随机相结合就是以下的模拟退火算法的思想。
- 思想:通过允许向不好的状态移动来避开局部最值点,但频率逐渐降低。
- 起源:冶金的退火原理。
- 退火用于对金属和玻璃进行回火或硬化。
- 将一个固体放在高温炉内进行加热,提升温度至最大值。在该温度下,所有的材料都处于液体状态,并且粒子本身随机地排列。随着高温炉内的温度逐渐冷却,该结构的所有粒子将呈现低能状态。
- 例子: 弹球的分析
- 剧烈的摇动(=高温)
- 减少晃动(=降温)
- 模拟退火是一种给定函数逼近全局最优解的概率方法。发表于 1953 年。
- 具体来说,是一种在大搜索空间逼近全局最优解的元启发式方法 。
优化与热力学
目标函数 x 能量极位
可接受解 x 系统状态
相邻解 x 状态变化
控制参数 x 温度
更优解 x 凝固状态
实现
- 初始解:使用随机选择启发式方法生成。
- 相邻节点:随机生成。当前解的变异。
- 接受条件:相邻节点具有较低代价值,具有较高代价值的相邻节点则以概率 P 接受。
- 停止判据:解具有比阈值低的值。已达到迭代最大总次数。
一种允许部分下山移动的随机爬山法的版本。下山移动在退火调度的早期容易被接受,随着时间的推移逐步降低。
模拟退火搜索的性质
- 可以证明: 如果 T 降低的足够慢,则模拟退火能以趋近于1的概率找到最优解。
-
3.2 遗传算法 Genetic Algorithms
基本思想
遗传算法的一些要素是1960年代提出的。通过约翰·霍兰在1970年代早期的工作,尤其是他的《神经元与人工系统的适应性》(1975年)一书,使得遗传算法流行起来。
它是一种模仿自然选择过程的搜索启发式算法。
遗传算法是局部束搜索的变形:与自然选择过程有些相似性,通过把二个父代结合产生后继(有性繁殖),而不是修改单一状态(无性繁殖)。
特点
遗传算法属于进化算法这个大分类。
- 该算法采用自然进化所派生的技法来生成优化问题的 解,例如遗传、 突变 、选择、以及杂交(inheritance , mutation , selection , and crossover)
- 通过结合两个状态来产生后续状态
- 该算法开始时从具有一组k 个随机产生的状态开始(种群,population)
- 每个状态(个体)表示成字符串 (染色体)
- 评估函数(适应值函数,fitness function)
- 通过选择,交叉和变异操作来产生新一代种群。
遗传算法的应用
- 生物信息学
- 计算科学
- 工程
- 经济学
- 化学
- 制造
- 数学
- 物理
- 种系遗传学
- 定量药理学
4. 群体智能
4.1 蚁群优化 (Ant Colony Optimization)
基本思想
- 它是一种解决计算问题的概率技术,可以用于发现一个图上的最佳路径。
- 最初是由Marco Dorigo于1992年在他的博士论文中提出的。
该算法是受蚂蚁在蚁巢和食物源之间寻找路径行为的启发而形成的。
蚁群优化的概念
蚂蚁从蚁巢到食物源之间盲目地游荡:
- 最短路径是通过费洛蒙嗅迹(pheromone trails)发现的
- 每个蚂蚁随机地移动
- 费洛蒙就遗留在路径上
- 蚂蚁察觉到前面蚂蚁的路径,跟随而去
-
蚁群优化算法
在路径段上积累“虚拟”嗅迹
- 开始时随机选择某个节点
- 随机选择一条路径:基于从初始节点至合适路径上出现嗅迹的量;具有较多嗅迹的路径则具有较高的概率
- 蚂蚁到达下一个节点后,再选择下一个路径
- 重复直到更多的蚂蚁在每个循环中都选择同一个路径
例: 旅行推销员问题Travelling Salesperson Problem (TSP)
- 一个推销员花时间访问 n 个城市。
- 他每次仅访问一个城市,最后回到他出发的地方。
他应该按什么顺序访问这些城市才能使距离最短?
TSP 的要点如下:不是 一个状态空间问题;
「状态」= 可能的旅行路线 = (n-1)!/ 2
TSP 是组合优化中的一个NP 难问题 ,在运筹学和理论计算机科学中非常重要
最早的蚁群优化算法旨在解决旅行推销员问题,其目标是找到连接所有城市的最短往返旅程。一般的算法相对简单,基于一群蚂蚁,每个都能够沿着这些城市形成一个可能的往返旅程。
蚁群优化的应用
- 进度安排问题
- 车辆路径问题
- 分派问题
- 物理设计中的设备量尺问题
- 图像处理中的边缘检测
- 数据挖掘
4.2 粒子群算法 (Particle Swarm Optimization)
粒子群优化 Particle Swarm Optimization(PSO)
由詹姆斯·肯尼迪和拉塞尔·埃伯哈特于1995年提出。受鸟类和鱼类的社会行为的启发。
- 采用若干粒子构成一个围绕搜索空间移动的群体来寻找最优解。
- 搜索空间的每个粒子根据它自己的飞行经验和其它粒子的飞行经验调整它的“飞行”。
Bird Flocking 鸟群
- 一群鸟在一个区域随机地寻找食物。
- 在该被搜索区域仅有一块食物。
- 但它们在经过每次环飞后知道食物有多远。
- 因此发现食物的最好策略是什么?
- 最有效的方法是跟随离食物最近的鸟。
- 仅需三个简单的规则
- 避免与相邻的鸟碰撞;
- 保持与相邻的鸟相同的速度 ;
- 靠近相邻的鸟。
PSO的应用
人工神经网络
- ANN 是一种大脑简单模型的计算范型,而反向传播算法是训练 ANN 的最受欢迎的方法之一。
- 已经有重要的的研究工作,为了改进 ANNs 的一个或多个方面,应用了进化计算计算(evolutionarycomputation (EC))。
- 若干篇论文报告了采用粒子群优化来替代 ANN 中的反向传播学习算法。
论文表明, PSO 是一种训练 ANN 的有前途的方法,它快速并且在多数情况下取得了更好的结果。
5. 小结
局部搜索:爬山法在完整状态形式化上进行操作;局部束搜索法保持k个状态的轨迹;禁忌搜索采用一种带约束的邻域搜索。
- 优化与进化算法:模拟退火在大搜索空间逼近全局最优解;遗传算法模仿自然选择的进化过程。
- 群体智能:蚁群优化可以寻找图的最好路径;粒子群优化通过迭代来改善一个候选解。
为了找出地球上最高的山,一群有志气的兔子们开始想办法。
- 兔子朝着比现在高的地方跳去。他们找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是爬山法,它不能保证局部最优值就是全局最优值。
- 兔子喝醉了。他随机地跳了很长时间。这期间,它可能走向高处,也可能踏入平地。但是,他渐渐清醒了并朝他踏过的最高方向跳去。这就是模拟退火。
- 兔子们知道一个兔的力量是渺小的。他们互相转告着,哪里的山已经找过,并且找过的每一座山他们都留下一只兔子做记号。他们制定了下一步去哪里寻找的策略。这就是禁忌搜索。
- 兔子们吃了失忆药片,并被发射到太空,然后随机落到了地球上的某些地方。他们不知道自己的使命是什么。但是,如果你过几年就杀死一部分海拔低的兔子,多产的兔子们自己就会找到珠穆朗玛峰。这就是遗传算法。

