4.0 搜索技术概述
引言:搜索技术概述 有这样一个问题,农夫、狼、羊、白菜刚开始在河的岸边,现在有一条船,要使他们全部过河,最终到达河的另一岸,但在过河时有三个限制条件:
- 只有农夫能开船
- 船上除了农夫外只能放一样物品
- 没有农夫看管时,狼会吃羊,羊会吃白菜
请问如果你是农夫,你该如何制定过河的策略?
- 在所有策略中:
- 究竟哪一种策略能够使农夫过河
- 哪一种策略使得过河的步骤最少
这就是搜索要解决的问题,搜索技术就是用搜索方法寻求问题解答的技术
搜索
搜索是实现人工智能的一个重要组成部分,它能使机器像人一样思考,它会影响到智能系统的性能和运行效率
搜索技术在人工智能领域有非常多的应用,在现实中能够解决许多问题,例如:
许多复杂的问题可以逐步解决,每走一步,问题就达到新的状态
- 当前状态和下一状态之间存在联系,做成图,就成为状态转移图
- 搜索的目标,就是在状态转移图中寻找最优的路线
如何搜索
盲目搜索
启发式搜索
在搜索中加入了与问题有关的启发性信息,使得机器能够更“聪明”地实现搜索,降低尝试的次数,每一步都尽可能选择最优路径,以最(较)快的速度找到问题的解。
博弈搜索
许多问题需要两人或者多人参与,在有对弈者参与的状态空间下进行的搜索称为博弈搜索,这种情况不仅要考虑自己每一步的策略,同时还要考虑对方可能执行的操作。
4.1 问题求解 Agent
1.1 人工智能中问题求解
- 解:是一个达到目标的动作序列。
- 过程:寻找该动作序列,称其为搜索。
- 问题形式化:给定一个目标,决定要考虑的动作与状态。
- 为何搜索:对于某些NP)完或者NP)难问题,只能通过搜索来解决。
- 问题求解智能体:是一种基于目标的智能体,通过搜索来解决问题。
1.2 简单的问题求解智能体的算法
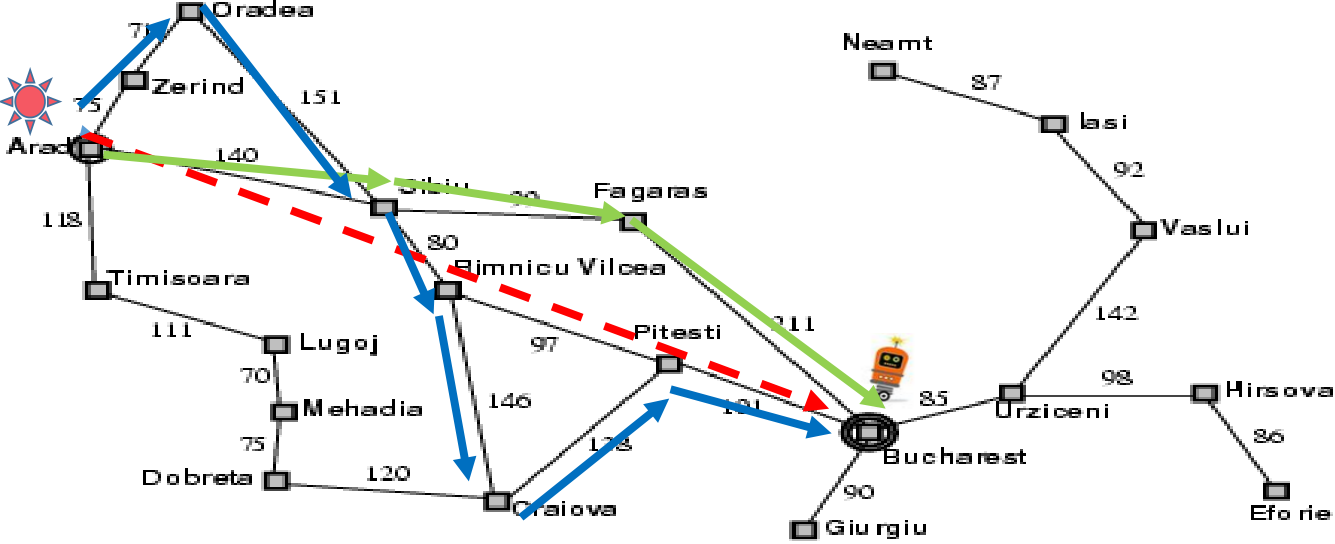
例子:罗马尼亚Romania度假问题
1.3 相关术语
相关定义
例如,该智能体位于Arad的初始状态可以记作:In(Arad).
- 动作:描述该智能体可执行的动作
ACTION(s)返回s状态下可执行的动作序列。例如,{Go(Zerind), Go(Sibiu), Go(Timisoara)}.
- 转换模型(后继函数):描述每个动作做什么
RESULT(s, a) 返回s,动作a之后的状态。例如,RESULT(In(Arad), Go(Zerind)) = In(Zerind)
- 目标测试:确定一个给定的状态是否是目标状态
例如 :智能体在 Bucharest的目标是单元素集合:{In(Bucharest)}.
- 路径代价:即每条路径所分配的一个数值代价
例如:状态s下执行动作a到达状态s’ 的步骤代价表示:c(s, a, s’).
4.2 问题实例
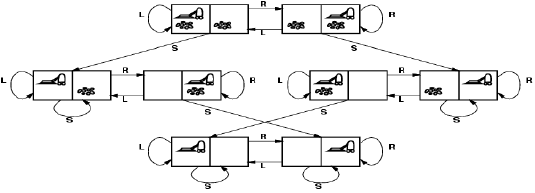
2.1 真空吸尘器世界状态空间图
- 状态:机器人的位置及灰尘位置
- 动作: 向左,向右,吸
- 转换模型:该动作应有的预期效果的预期效果(除无效动作)
- 目标测试:所有位置都干净
- 路径代价:每做一个动作计代价为1
2.2 八数码问题(九宫问题)
问题描述
3×3棋盘上有8个数字棋子和一个空格。与空格相邻的滑块可以移向该空格,目的是达到一个指定的目标状态。
8数码难题属于滑块数码难题家族,这个难题家族,这个被 认为是 NP-完的。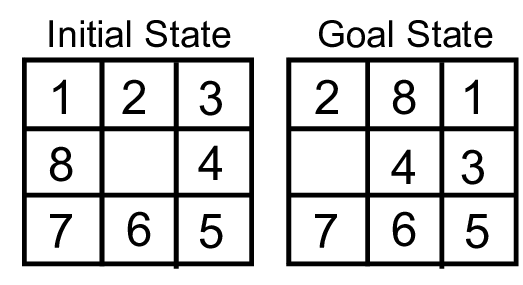
- 状态: 8个数字块的放置情况
- 动作:空格向上,向下,向左,向右移动
- 转换模型:移动后,产生数字块和空格的互换
- 目标测试: 目标状态(给定的)
- 路径代价: 每移动一步代价为1
数码的问题空间与运行时间:
- 8-puzzle → 9! = 362,880 states 0.036 sec
- 15-puzzle → 16! ~ 2.09 x 1013 states 55 hours
- 24-puzzle → 25! ~ 1025 state >
years
2.3 八皇后问题
问题描述
八皇后问题是一个以国际象棋为背景的问题:如何能够在8×8的国际象棋棋盘上放置八个皇后,使得任何一个皇后都无法直接吃掉其他的皇后,为了达到此目的,任两个皇后都不能处于同一条横行、纵行或斜线上。
八皇后问题可以推广为更一般的n皇后摆放问题:这时棋盘的大小变为n×n,而皇后个数也变成n。当且仅当n = 1或n ≥ 4时问题有解。
N皇后问题启示:
- 特点:一个解是最终的节点而不是一条路径;
- 状态空间的数目:100个皇后问题初始状态有10400个状态,改进后为1052,但仍然是很大;
- 但是通过对状态空间分布的研究可以很好的解决n很大的皇后问题。
求解智能体问题四个基本步骤:
形式化——搜索——执行
- 目标形式化(Goal formulation)
成功的状态描述
- 问题形式化(Problem formulation)
根据所给的目标考虑行动和状态的描述
一个问题可以由四个组成部分来形式化:
- 初始状态
- 动作
- 转换模型或后续函数
- 目标测试
- 路径代价
- 搜索(Search)
通过对行动序列代价计算来选取最佳的行动序列.
- 执行(Execute)
给出 “解”执行行动.
一个解是从初始状态到目标状态的动作系列: 解、代价、耗散值、最优解、无解
4.3 通过搜索求解
3.1 问题求解的方法
- 搜索状态空间(记住空间的复杂性取决于状态表示)
- 通过显式生成树搜索
- 根=初始状态。
- 节点和叶子通过后继函数生成。
- 在一般的搜索生成图(相同的状态,通过多条路径)
3.2 采用树搜索方法
- 基本思想: 通过产生已经探索到的状态的后续状态的方法来离线地进行状态空间的模拟搜索。
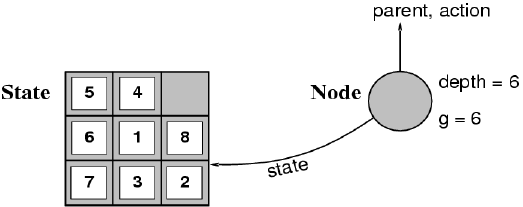
- 状态是一个物理配置的表示
- 节点是一个数据结构,包含:状态、父亲节点、动作、路径代价和深度
fringe (亦称open list):一种数据结构,用于存储所有的叶节点 explored (亦称closed list):一种数据结构,用于存储每个已扩展节点 该算法中采用,将在explored或fringe中的曾出现过的节点丢弃的方法。
3.3 采用图搜索方法
通过图搜索在该罗马尼亚地图上生成一系列搜索路径。
每个路径在每个阶段 通过每一步加以扩展。
注意在第 3 阶段,最北部城市 (Oradea)的后继节点均已出现过,所以,相当于成为一个dead end.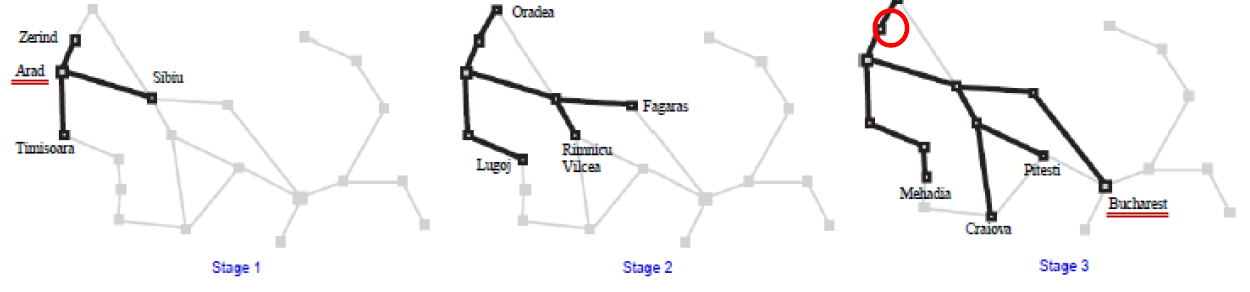
4.4 无信息搜索策略
简介
- 无信息搜索(又名盲目搜索),在搜索时,只有问题定义信息可用。
- 有信息的搜索:在搜索时,当有策略可以确定一个非目标状态比另一种更好的搜索。
- 盲目搜索策略仅利用了问题定义中的信息,所有的搜索策略是由节点扩展的顺序加以区分。
搜索策略评价
- 搜索策略
指节点扩展顺序的选择。
- 搜索策略的性能由下面四个方面来评估:
- 完备性: 如果问题的解存在时它总能找到解。
- 时间复杂性: 产生的节点个数。
- 空间复杂性: 搜索过程中内存中的最大节点数。
- 最优性: 它总能找到一个代价最小的解。
- 问题难度的定义:
- 由时间和空间复杂度的定义来度量的:
时间和空间复杂度根据下面三个量来表达:
- b: 搜索树的最大分支数
- d: 最小代价解所在的深度
- m: 状态空间的最大深度(可能是∞)
4.1 宽度优先搜索
搜索策略
优先扩展最浅层的未扩展节点实现方法
Fringe表采用先进先出队列( FIFO queue),即新的后续节点总是放在队列的末尾性能指标
- 完备性:具备 (只要 b 是有限的)
- 时间:
- 空间:
-
缺点
空间是一个比时间更严重的问题.
指数复杂性的搜索问题不能通过无信息搜索的方法求解。(除了规模极小的数据)
4.2 一致代价搜索
搜索策略
实现方法
性能指标
在单步代价相等时与宽度优先搜索一样
完备性: Yes, 只要单步代价不是无穷小
- 时间: 代价小于最优解的节点个数,
最优解的代价
是至少每个动作的代价
取上整
- 空间: 代价小于最优解的节点个数,
-
4.3 深度优先搜索
搜索策略
实现方法
实现:fringe = 后进先出队列(LIFO queue)
性能指标
完备性: No: 在无限状态空间中不能保证找到解
- 时间:
- 空间?
, i.e., 线性空间!
-
4.4 深度优先改进
递归实现
完备性: No
- 时间: O(bl)
- 空间: O(bl), i.e., 线性空间!
-
迭代深入
深度有限搜索(Deep limited search, DLS)搜索到d层时产生的节点数:
迭代深入搜索(iterative deepening search ,IDS)搜索到d层时产生的节点数: 完备性: Yes
- 时间: (d+1)b0 + d b1 + (d-1)b2 + … + bd = O(bd)
- 空间:
-
4.5 双向搜索
搜索策略
实现方法
检查当前节点是否是其他fringe表的节点。
- 每个节点的前状态应是有效的可计算。
- 行动是容易可逆的。
性能指标
如果双向都采用宽度优先则算法是完备的和最优性的.
比较 b=10 以及 d=6 的问题扩展节点数:缺点
空间复杂度仍然是最大的问题4.6 无信息搜索的比较
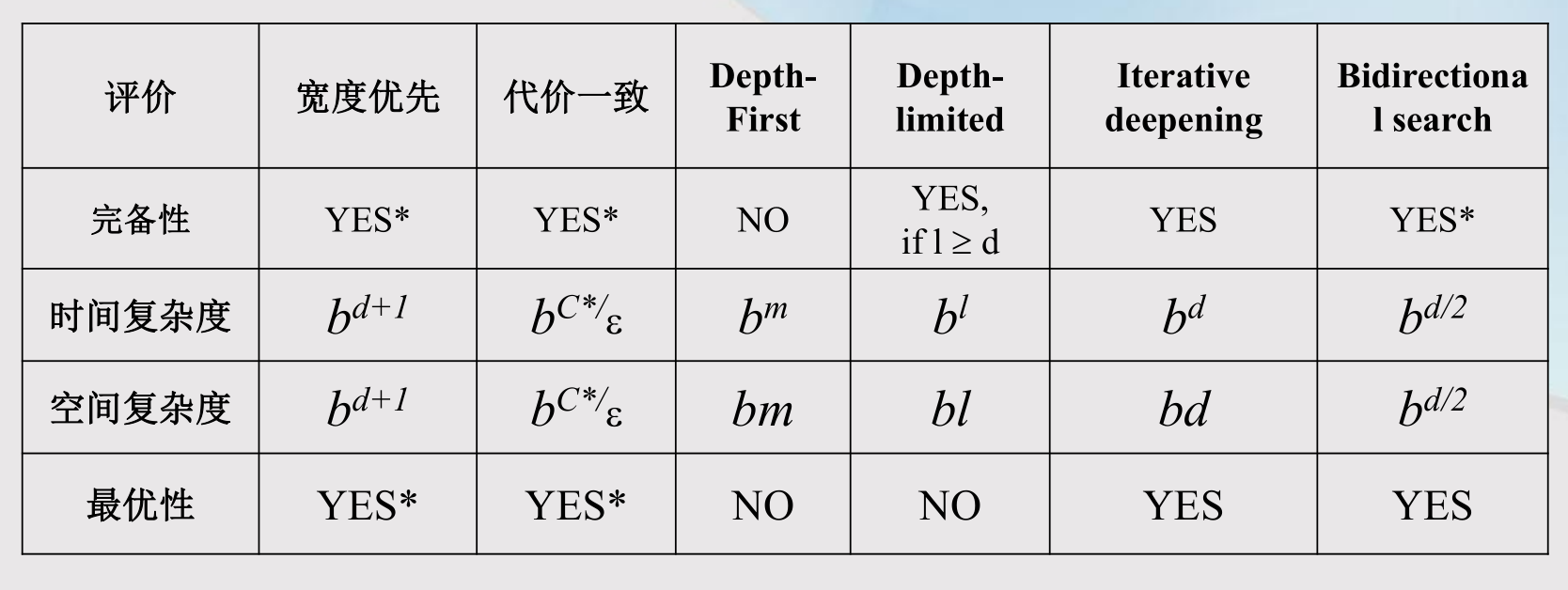
重复状态
如果不能检测重复的状态,会导致把一个线性空间问题变成指数级的问题(不可解)。
4.7 图搜索
性能指标
- 完备性:是的
- 最优性:
- 图搜索截断了新路径,这可能导致局部最优解。
- 当单步代价相同宽度搜索或代价一致的搜索时是最优的。
- 时间和空间复杂度:
- 与状态空间的大小成比例的(可能远远小于O(bd))
- 深度和迭代深度搜索算法不再是线性空间。(因为,需要保存explored表)。
4.8 无信息搜索课堂思考题
传教士和野人问题M-C问题(Missionaries & Cannibals Problem)
- 已知:传教士人数M=3,野人人数C=3,一条船一次可以装载不超过2人K<=2。
- 条件:任何情况下,如果传教士人数少于野人人数则有危险。
- 问题:传教士为了安全起见,应如何规划摆渡方案,使得任何时刻,河两岸以及船上的野人数目总是不超过传教士的数目。
即求解传教士和野人从左岸全部摆渡到右岸的过程中,任何时刻满足:M(传教士数)≥C(野人数)和M+C≤k的摆渡方案。
- 要求:
- 形式化该问题,并计算状态空间大小;
- 应用无信息搜索算法求解;(考虑重复状态?)
- 这个问题状态空间很简单,你认为是什么导致人们求解它和困难?
4.5 有信息搜索策略
无信息搜索又名盲目搜索:
- 在搜索时,只有问题定义信息可用。
- 盲目搜索策略仅利用了问题定义中的信息。
有信息搜索:
思想:
使用一个评估函数 f(n)给每个节点估计他们的希望值。 优先扩展最有希望的未扩展节点。
- 实现:fringe表中节点根据评估值从大到小排序
- 最佳优先搜索策略有:
- 贪婪最佳优先搜索
- A* 搜索
贪婪最佳优先搜索
- 贪婪最佳优先搜索优先扩展看上去更接近目标的节点(启发式函数评估出来的)
评估函数: f(n) = h(n) (heuristic,启发函数)
= 估计从节点n到目标的代价
例如:hSLD(n) = 从节点 n 到 Bucharest的直线距离
性能
完备性? No – 可能陷于死循环当中
- 时间?O(bm), 但一个好的启发式函数能带来巨大改善
- 空间?O(bm)
-
A* 搜索
5.2 A*算法
思想
评估函数
f(n) = g(n) + h(n)
g(n) = 到达节点n已经发生的实际代价
- h(n) = 从节点n到目标的代价估计值
f(n) =评估函数,估计从初始节点出发,经过节点n,到目标的路径代价的估计
可采纳的启发式函数(admissible heuristic):
如果启发式函数h(n)对于任意的节点n都满足 h(n) ≤ h(n),这里 h(n)是指从节点n到达目标的真正代价,则称h(n)是可采纳的(admissible heuristic)。
定理: 如果h(n)是可采纳的,则 A* 树搜索算法是具有最优性。
A* 的最优性证明
性能指标
完备性?Yes
- 时间?指数级
- 空间?将所有产生的节点存储在内存中
- 最优性?Yes(如果h(n)是可采纳的)
5.3 A*的改进方法
存储受限制的启发式搜索
思想:迭代加深的A*算法,用一个f-cost代替有限制的深度优先中的d作为截断值,进行剪枝。递归最佳优先搜索(RBFS)
尝试模拟标准的最佳优先搜索而只需线性空间。
- 最优性:同A*一样,如果h是可采纳的,则有最优性;
- 空间复杂度:线性的O(bd);
- 时间复杂度:难以描述:取决于h的精确和最佳路径变换的次数。
存储限制的A* (简单)
思想
利用所有可以用的内存;扩展所有最佳节点直到内存满了;当内存满了,摘掉最差的那些叶子(当内存满了的时候删除最坏的节点);将该节点值备份到父节点中;
如果所有的节点都有相同的 f值怎么办?
某些节点被选出了扩展或被删除;简化的存储限制通过扩展新节点和删除最老的节点来简化处理。
(这是什么思想?深度还是宽度?)
性能
如果有解,简化的存储限制是完备的,也有最优性。
可采纳的启发式函数分析
对于 8-数码问题
- h1(n) = 错放的数字块个数
- h2(n) =状态n到目标状态的曼哈顿距离
占优势的启发式函数-启发性(控制能力)
有效分支因子b*
- 如果A算法生成的总节点数是N,在解深度为d的一致,树中所必须的分支因子b(含有N+1个节点)即有:
对于足够难的问题,该度量值是相当稳定的。
- 因此,在小规模问题集合上实验测量出的b*值,可以为研究启发式的有效性提供很好的指导。
- 一个好启发式的b*是接近1的。
5.4 如何构建启发函数
源自简化版问题的一个精确解
可采纳的启发式可以源自简化版问题的一个精确解。称为松弛问题:
对原定问题的动作的约束放宽,以松弛化问题的最优解的代价来定义原问题的一个可采纳启发式函数。
- 对于h1来说松弛8数码问题:一个牌可以移到任意的位置。因此,h1是这个问题最短路径解。
- 对于h2来说松弛8数码问题:一个牌可以移到任一相邻的位置。因此,h2是这个问题最短解。明显的, 一个松弛问题的最优解一定不会大于真实问题的最优解。
- 可采纳的启发式可以从原问题的子问题的一个解得到。
- 这个代价是真实问题代价的下界.
- 将每个可能的子问题实例的精确解存储起来作为一个模式数据库.
-
从经验中学习
经验=求解大量的8数码游戏。
例如:8数码的f(n)=g(n)+p(n)+3s(n)效率最高.
5.5 小结
- 最佳优先搜索:f(n)=g(n)+h(n)
- 贪婪最佳优先搜索: f(n)=h(n)
- A 搜索: 其中h(n)≤h(n)是可采纳的。
- A*的改进
- 启发函数的启发能力:
- 可采纳启发式设计:松弛问题 模式数据库 学习机制
6. 超越经典搜索
作业
编程实现:罗马尼亚度假问题,编程语言自选,输入罗马里亚简化地图
搜索策略
分别采用并比较算法性能: