1. CSPs 问题 (Constraint satisfaction problems
1.1 约束满足问题定义
相关概念
- 标准搜索问题: 状态是一个黑盒,通过后续函数,启发式函数和目标测试来访问。
CSP:
- 状态由多个变量Xi定义,变量Xi的值域为Di
- 目标测试是由约束集来确定,约束指定变量子集允许的赋值组合。
CSP形式化:
- 有限变量集:{X1, X2, …, Xn}
- 有限约束集:{C1, C2, …, Cm}
- 每个变量有非空可能值域:Dx1, Dx2, … Dxn
- 每个约束Ci的值可以用变量来表示:例如X1 ≠ X2
- 一个状态被定义为所有变量的赋值
一个相容的赋值:所有赋值均满足所有约束
例子: 地图着色问题
- 变量: WA, NT, Q, NSW, V, SA, T
- 域: Di = {red,green,blue}
- 约束:相邻区域不能着相同的颜色
- 解是完整而且符合约束的赋值,
如: WA = red, NT = green, Q = red, NSW = green, V = red, SA = blue, T = green
一些CSP问题要求一个目标函数的最佳解。
约束图:
- 二元CSP:每个约束都关联两个变量
- 约束图:结点表示变量,边表示约束
- CSP的特点(优势)
- 呈现出标准的模式
- 通用的目标和后继函数
- 通用的启发函数(无域的特别技术)
CSP的变量类型
- 离散变量
- 有限域:
- n 个变量, 域大小为d O(dn)
- 无限域:
- 作业调度,变量是工序的起始和结束日期
- 约束:StartJob1 + 5 ≤ StartJob3
- 有限域:
- 连续变量
- 哈勃太空望远镜观测的起始和结束时间
变量约束类型
- 一元约束只涉及到一个变量
- e.g., SA ≠ green
- 二元约束涉及到两个变量
- e.g., SA ≠ WA
- 高阶约束涉及到3个以个的变量
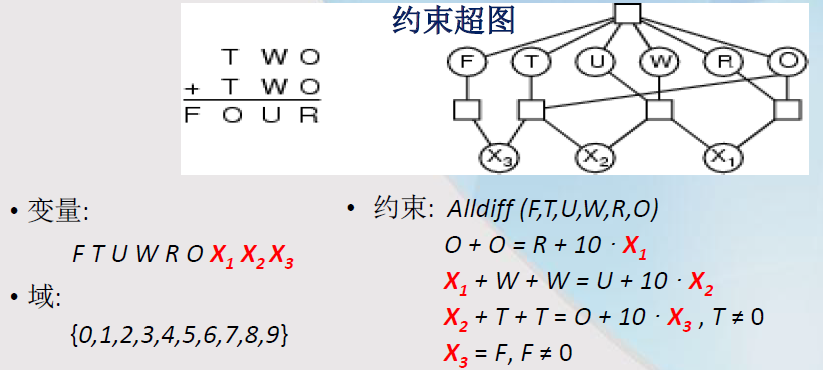
- e.g.,密码算术约束
- 偏好约束
真实世界CSPs
状态用已经给变量赋的值来表示
- 初始状态: 空{ }
- 后续函数:给一个没有赋值的变量赋值,此值与已经赋的值不能与约束冲突。
- 目标测试:当前赋值是完整赋值,即所有变量都有值。
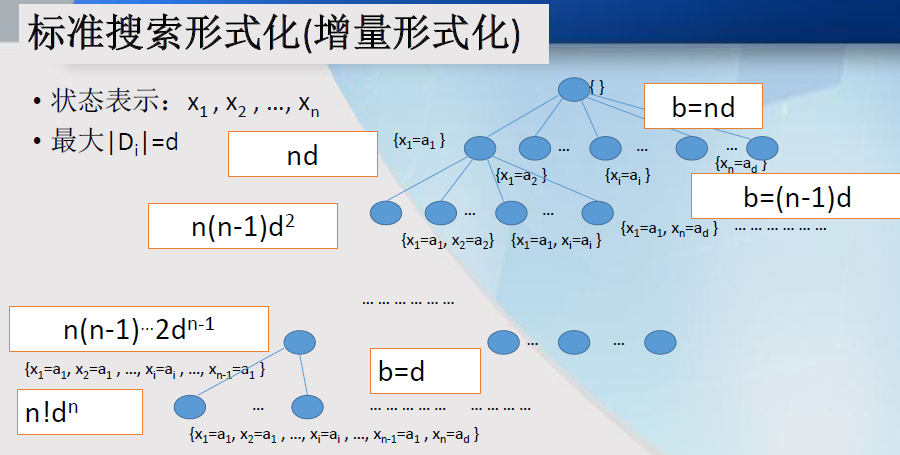
标准搜索形式化CSP(增量形式化)
- 有n个变量的问题,解都在深度为n 的层 → 可以使用深度优先搜索
- 在深度为l 时,分支数b = (n - l )d ,所以搜索树有n! ·dn 个叶子结点
1.3 回溯搜索算法求解CSP
- 变量赋值是可交换的, i.e.,
[ WA = red then NT = green ] 等同于[ NT = green then WA = red ]
- 每个结点只需要考虑给一个变量赋值 → b = d 所以dn片叶子
- 采用单变量赋值的深度优先搜索称为回溯搜索
通用方法就能巨大提高效率:
- 下一步应该给哪个变量赋值?
- 应该以一种什么顺序来试着给变量赋值?
- 能不能早些检测到不可避免的失败?
回溯改进——最大受限变量
- 最大受限变量( most constrained variables):具有最少合法赋值的变量
- 也称为最少剩余值启发式(minimum remaining values ,MRV)
- 当多个变量的MRV 值相同时, 采用最大约束准则Most constraining variable)从中选择
-
回溯改进——最少约束值
选择好了变量后,选择一个最少约束值来尝试赋值
-
前向检查
我们如何较早探测到不可避免的失败?——并且在后面避免它。
- 向前检查的思想:只保留未赋值的变量的合法值。
- 当任何变量出现没有合法可赋值的情况终止搜索。
- 跟踪未赋值变量的合法赋值,当发现有变量没有合法赋值时就停止搜索
Example: 4-Queens Problem
约束传播
- 前向检查把已经赋值变量的信息传播给未赋值变量,但不能提早检测到所有失败。
- NT 和SA 不能同时为蓝色
向前检验不能检测出该类矛盾,因为它看得不够远。
约束传播是将一个变量的约束内容传播到其它变量上的方法。
……
弧相容(Arc consistency)
- 弧相容原则能比前向检查更早检测到失败
可以在变量赋值前或后进行弧相容检查
弧相容依然不能探测出所有的不相容
- 一种K-相容的概念可以定义更强的约束传播方式
- 如果对于任何k-1个变量的相容赋值,第k个变量总能被赋予一个和前k-1个变量相容的值,那么这个csp就是一个k相容的。
- 例如:
1-相容是指每个单独的变量,自己是不矛盾的,也称为节点相容。
2-相容就是弧相容。
3-相容是指任何一对相邻的变量总可以扩展到第三个邻居变量,也称为路径相容。
K-相容的只有当它是K-相容,也是(K-1)-相容,(K-2)-相容,…,直到1-相容
- 弧相容算法AC-3时间复杂度: O(n2d3)
- 对这样的K-相容是理想化的(完美的)。因为,一个解可以在
内找到,而不是
。
- 但在最坏的情况下建立任何一个n-相容算法需要花费n的指数级时间。
进一步的改进: 检查特别的约束(以下2种代表)
- Alldif(…)约束:在要求涉及的全部变元都必须取不同的值时
- 如果约束涉及m个变元,它们共有n个不同的取值,如果有m>n,那么这个约束不可满足,要及早停止。
- 算法思想:
首先,删除约束中只有一个取值的变元;然后,将这个值也从值域中删除;
循环执行上的步骤,直到得到一个空值域或者剩下的变量数比可取值的个数多,则产生矛盾。
- Atmost(…)至多约束:对于每个变量X和它的取值的上、下界,每个变量Y都存在某个取值满足X和Y之间的约束,我们称该CSP为边界相容的。
- 这种边界传播广泛地应用于实际的约束问题中。
局部搜索算法解决CSPs
1.4 局部搜索算法求解CSPs
- 局部搜索应用到约束满足问题CSPs:
- 采用完全形式化表示(即允许状态不符合约束)
- 动作定义为:给变量重新赋值(对不满足约束的变量)
- 变量选择:随机选择一个违反约束的变量重新赋值
- 赋值方案采用最少冲突启发式原则,即选择违反最少约束的值进行赋值操作
例子: 4皇后问题
- 状态:每列摆放一个皇后(44 = 256 个不同状态)
- 动作: 将皇后在同一列内移动
- 目标测试: 互相攻击不到
- 评估函数: h(n) = 攻击到的皇后对数
任意给定一个初始状态,局部搜索算法能以很高的概率在常数时间内解决大规模n皇后问题(e.g., n = 10,000,000)
效果:
- 最小冲突法几乎是独立于问题的规模的。
- 可以在大约50步以内解决百万皇后的问题。
-
2. 联机搜索
到如今为止,我们探讨的都是非实时的,或称为脱机问题。
脱机问题(offline)=它们在执行前就可以计算出解决方案
- 联机问题(online)=它们在执行时,需要计算和行动交叉进行
- 联机搜索对于动态和半动态环境的搜索问题是必须的;
- 现实,在搜索过程中考虑所有的可能的偶发事情是不可能的。
- 常见的探究问题:
- 智能体在未知的状态以及行为。
e.g. 一个新生儿, 机器人在一个新环境, …
- 假设智能体有以下的知识:
- ACTION(s): 状态s下可能的行动列表函数
- C(s,a,s’): 单步耗散(直到智能体s知道行动的结果s’时才能得到!)
- GOAL-TEST(s):目标测试
- 事实:智能体能够记住先前的状态,不能访问下个状态。
- 行动是确定的。
- 可以使用可采纳的启发函数h(s)
e.g. 曼哈顿距离
- 目标:用最小耗散达到目标
- 耗散:整个路径的总耗散
- 竞争率=实际代价同如果已知搜索空间的解路径代价的比值。
- 当智能体偶然达到死路径可能造成无限循环。
- 一个联机智能体具有维护环境地图能力
- 随着输入的感知更新地图
- 并应用它确定下一个行动
同A*算法的区别
局部搜索:爬山法在完整状态形式化上进行操作;局部束搜索法保持k个状态的轨迹;禁忌搜索采用一种带约束的邻域搜索。
- 优化算法:模拟退火在大搜索空间逼近全局最优解;遗传算法模仿自然选择的进化过程。
- CSP问题:是一类特别的问题:状态是通过对变量集的赋值,目标测试是通过变量值的约束定义。
- 联机问题: