是不是稳定的定义就是看具有相同字段的相对位置是不是遭到破坏稳定的排序算法：简单的理解就是，能保证排序前2个相等的数所在序列的前后相对位置顺序和排序后它们两个的前后位置顺序相同。如果A1 = A2，A1原来在位置前面，排序后A1还是保持在A2位置前。不稳定的排序算法：排序前后在序列中的相对位置发生变化。

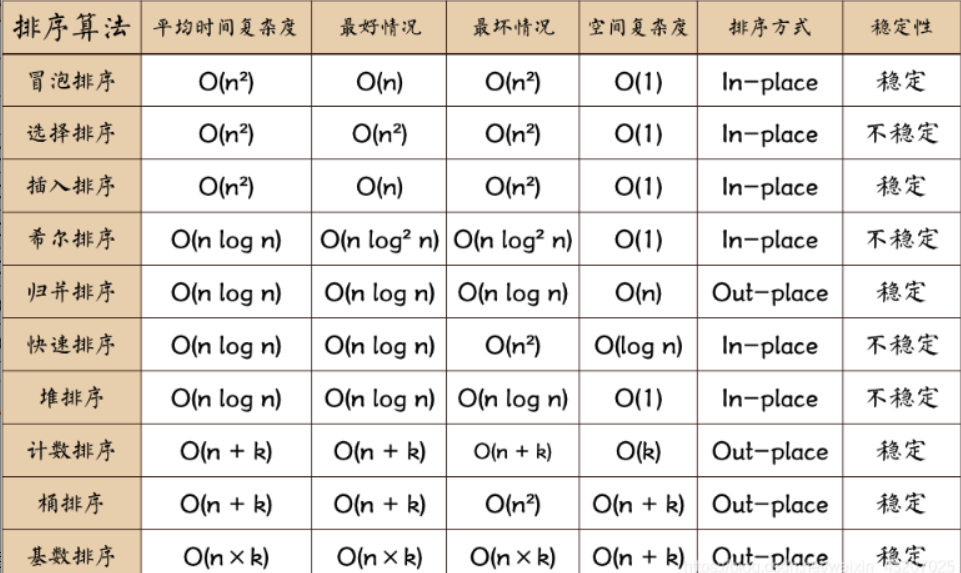
冒泡排序

平均时间复杂度是O（n²）：逆序排列
最好情况是O（n）：当输入的数据已经有序时，只需遍历一遍用于确认数据已有序
最坏情况是O（n²）
空间复杂度是O（1）
稳定性是稳定的：因为每次比较后如果两个相邻元素相等我们并不会将他们交换，
所以冒泡不会改变相同元素的下标，所以冒泡排序是一个稳定的排序。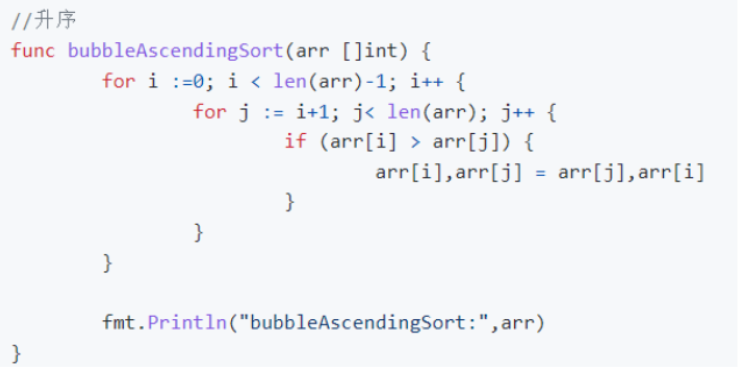

只遍历一次

选择排序

解法：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。
平均时间复杂度是O（n²）
最好情况是O（n²）
最坏情况是O（n²）
空间复杂度是O（1）
稳定性是不稳定的：举个例子，序列5 8 5 2 9，我们知道第一遍选择第1个元素5会和2交换，
那么原序列中2个5的相对前后顺序就被破坏了，所以选择排序不是一个稳定的排序算法

func SelectSort(arr []int) {
    n := len(arr)
    for i := 0; i < n; i++ {
        minIndex := i
        for j := i+1; j < n; j++ {
            if arr[j] < arr[minIndex] {
                minIndex = j
            }
        }
        if minIndex != i {
            arr[minIndex], arr[i] = arr[i], arr[minIndex]
        }
    }

插入排序

从第一个元素开始，该元素可以认为已经被排序，取出下一个元素，在已经排序的元素序列中从后向前扫描，如果该元素（已排序）大于新元素，将该元素移到下一位置，重复步骤，直到找到已排序的元素小于或者等于新元素的位置。
平均时间复杂度是O（n²）
最好情况是O（n）：当输入的数据已经有序时，只需遍历一遍用于确认数据已有序
最坏情况是O（n²）：完全逆序
空间复杂度是O（1）
稳定性是稳定的

func InsertSort(arr []int) {
    n := len(arr)
    for i := 0; i < n-1; i++ {
        if arr[i+1] < arr[i] {
            for j := i+1; j > 0 && arr[j] < arr[j-1]; j-- {
                arr[j], arr[j-1] = arr[j-1], arr[j]
            }
        }
    }
}

希尔排序

基于插入排序改进的，插入排序每次只能将数据移动一位。希尔排序是一种分组插入方法
第一步：分组。按一定的间隔分组，然后组内排序（尽量间隔取总长的一半，这样每组就是两个元素）
第二步：重新设置间隔分组，继续组内排序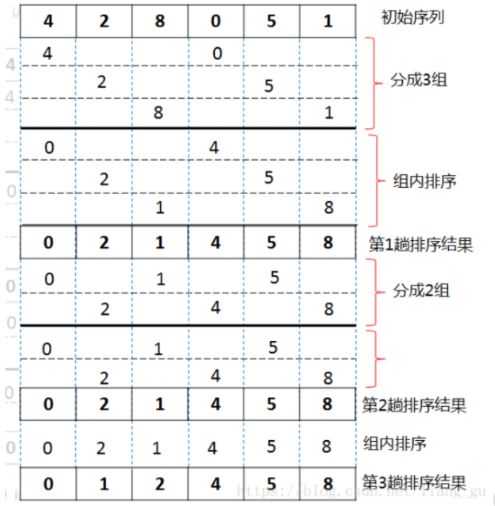

平均时间复杂度：T(n) = O(nlogn)
最坏时间复杂度：T(n) = O(nlog²n）
最坏时间复杂度：T(n) = O(nlog²n）
空间复杂度: O(1)
稳定性: 不稳定，由于多次插入排序，我们知道一次插入排序是稳定的，不会改变相同元素的相对顺序，
但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所
以shell排序是不稳定的。

func ShellSort(arr []int) {
    n := len(arr)
    increment := n
    for true {
        increment = increment/3 + 1
        for i := 0; i < increment; i++ {
            for j := i + increment; j < n; j+=increment {
                for k := j; k > i && arr[j] < arr[j-increment]; k-=increment {
                    arr[k], arr[k-increment] = arr[k-increment], arr[k]
                }
            }
        }
        if increment == 1{
            break
        }
    }
}

二分查找

func BinarySearch(arr []int, val int) int {
    l, r := 0, len(arr)-1
    for l <= r {
        mid := (l + r)/2
        tmp := arr[mid]
        if tmp == val {
            return mid
        } else if val < tmp {
            r = mid - 1
        } else {
            l = mid + 1
        }
    }
    return -1
}