77. 组合
题目描述
给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。你可以按 任何顺序 返回答案。
思路
我们可以把组合问题抽象为以下树形结构：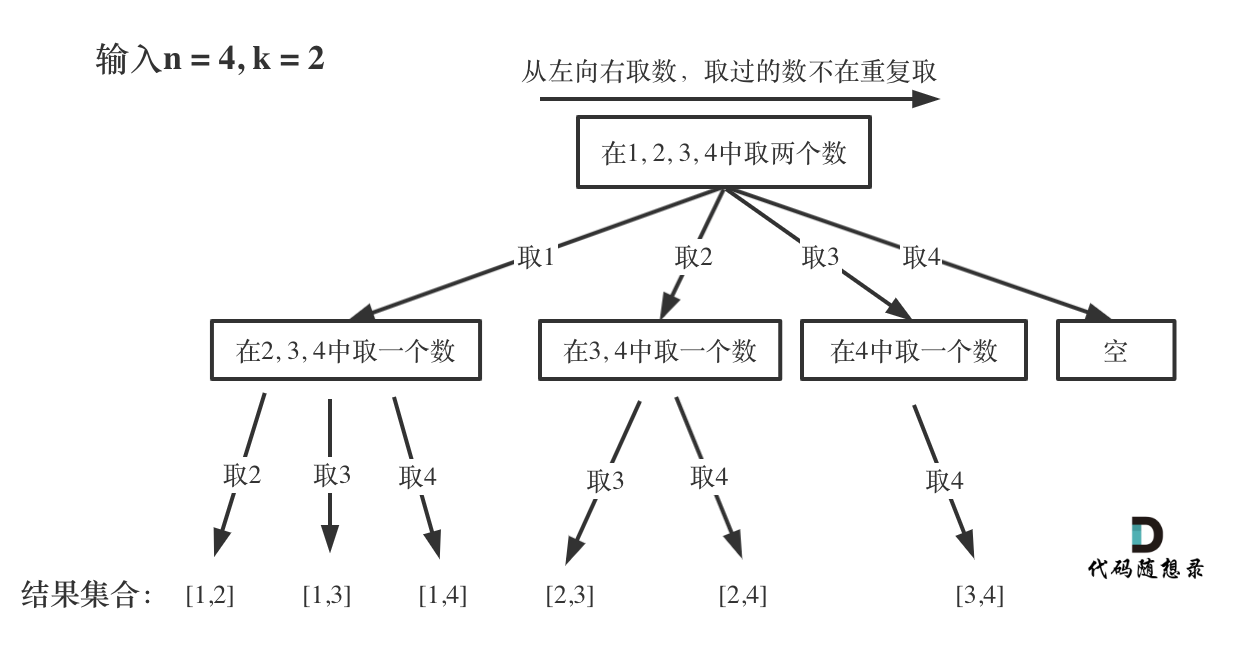
从上图可以看出，首先在[1 2 3 4 ]中取一个数，每一个数都要取一次，所以这里有个大的for循环。for i := 0; i < n ;i++
比如，取了1以后，下面在第一次取1的这个情况下进行操作。
for i := start;i <= n;i++{path = append(path,i)backtracing(n,k,i+1,path)path = path[:len(path)-1]}
当 i 取1以后开始对[2 3 4]进行取值，这里进行一下i+1，取到了2（注意这时候是在for i := 1; i < n ;i++）。这时候path里面有了2个数和k相等，这时候就要返回，第一次返回以后这时候path=[ 1 2 ]，然后走path = path[:len(path)-1]这条代码，path = [ 1 ]。for i := 1; i < n ;i++这个循环才进行一次，下一轮i = 2，path取到了3，path = [ 1 3 ]，这时候因为进行到了最后一层，所以这个循环每一次进行完以后，就会返回，path不断进行删除和添加元素操作。当这一轮的for i := 1; i < n ;i++循环走完以后。注意：每一次的添加元素和删除元素成对出现的，所以，在i取1的这个大前提下，所进行的后面每一个对path的操作都是添加删除。也即是一直在backtracing(n,k,i+1,path)这里面进行操作的。这时候backtracing(n,k,i+1,path)执行完毕后，继续执行path = path[:len(path)-1]，把1从path中删除，path为空数组。下一大轮次i就取2了。如此反复。
优化
来举一个例子，n = 4，k = 4的话，那么第一层for循环的时候，从元素2开始的遍历都没有意义了。 在第二层for循环，从元素3开始的遍历都没有意义了。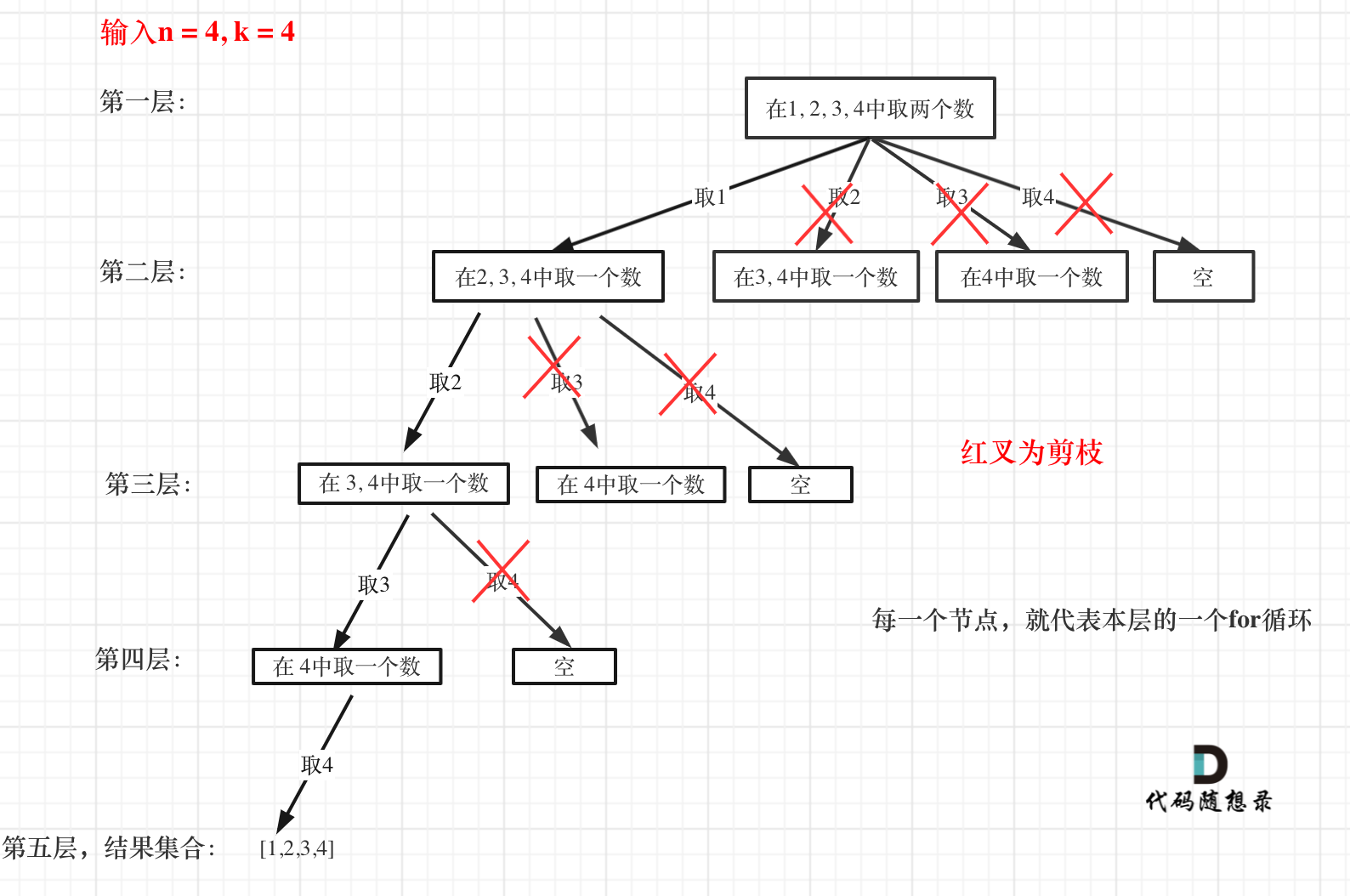
图中每一个节点（图中为矩形），就代表本层的一个for循环，那么每一层的for循环从第二个数开始遍历的话，都没有意义，都是无效遍历。
优化过程如下：
- 已经选择的元素个数：
len(path) - 还需要的元素个数为:
k - len(path) - 在集合n中至多要从该起始位置 :
n - (k - len(path)) + 1，开始遍历，为什么有个+1呢，因为包括起始位置。
举个例子，n = 4，k = 3， 目前已经选取的元素为0，n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。
从2开始搜索都是合理的，可以是组合[2, 3, 4]。
所以优化之后的for循环是：for i := start;i <= n - (k - len(path)) + 1;i++
运行代码
var res [][]intfunc combine(n int, k int) [][]int {res = [][]int{}if n <= 0 || k <= 0 || k > n {return res}backtracing(n, k, 1, []int{})return res}func backtracing(n,k,start int,path []int){if len(path) == k{temp := make([]int,k)copy(temp,path)res = append(res,temp)return}for i := start;i <= n - (k - len(path)) + 1;i++{path = append(path,i)backtracing(n,k,i+1,path)path = path[:len(path)-1]}}
上面需要注意的是，当长度等于K的时候，不可以直接res = appen（res, path），因为res中存放的是path切片，res[ 0 ] = path，res[ 1 ] = path，res[ 2 ] = path.....这样之后每次对path修改都是对切片进行修改，同时肯定就伴随着会修改res内部元素。也即出现这样的结果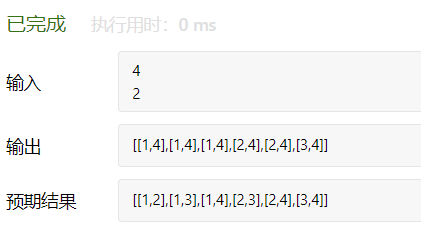
只会记录最后一次对path的修改。
为了避免这种情况我们采用代码中写法，把每一时刻的path记录下来。
216.组合总和III
题目描述
找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：
只使用数字1到9
每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。
思路
大体思路和上一题77.组合差不多。各部分解释如下：
for 循环是从1到9，k还是不变，引入一个sum。其实就只是在终止条件哪里有一点变化。
运行代码
var res [][]intfunc combinationSum3(k int, n int) [][]int {res = [][]int{}if n <= 0 || k <= 0 || k > n{return res}backtracking(n,k,1,[]int{},0)return res}func backtracking(n,k,start int,path []int,sum int){if len(path) == k{if sum == n{temp := make([]int,k)copy(temp,path)res = append(res,temp)}return}for i:=start;i<=9-(k-len(path))+1;i++{sum += ipath = append(path,i)backtracking(n,k,i+1,path,sum)sum -= ipath = path[:len(path)-1]}}
17.电话号码的字母组合
题目描述
给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。
提示：
- 0 <= digits.length <= 4
- digits[i] 是范围 [‘2’, ‘9’] 的一个数字。
思路
例如：输入：”23”，抽象为树形结构，如图所示：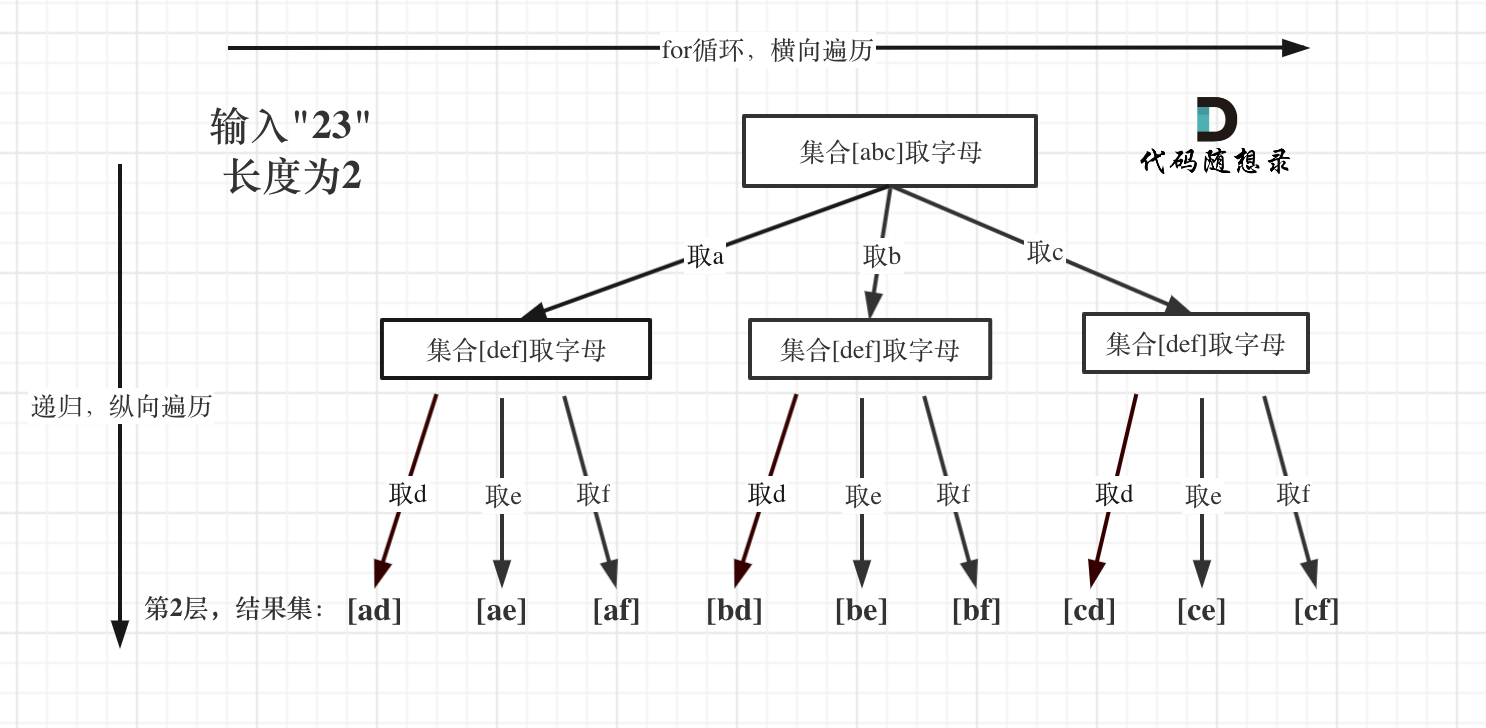
当在第一层取一个字母的时候，第二层就是第二个数字对应的字母。运行代码
var res []stringfunc letterCombinations(digits string) []string {length := len(digits)if length == 0 || length > 4{return nil}digitsMap := [10]string{"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"}res=make([]string,0)backtracking("" ,digits, 0,digitsMap)return res}func backtracking(tempString ,digits string, Index int,digitsMap [10]string){if len(digits) == len(tempString){res = append(res,tempString)return}tmpK:=digits[Index]-'0'letter:=digitsMap[tmpK]for i:=0;i<len(letter);i++{tempString=tempString+string(letter[i])//拼接结果backtracking(tempString,digits,Index+1,digitsMap)tempString=tempString[:len(tempString)-1]//回溯}}
39. 组合总和
题目描述
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有不同组合 ，并以列表形式返回。你可以按任意顺序返回这些组合。
candidates 中的同一个 数字可以无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。
对于给定的输入，保证和为 target 的不同组合数少于 150 个。
思路
这道题可以无限制重复选取数组元素，具体思路如下图：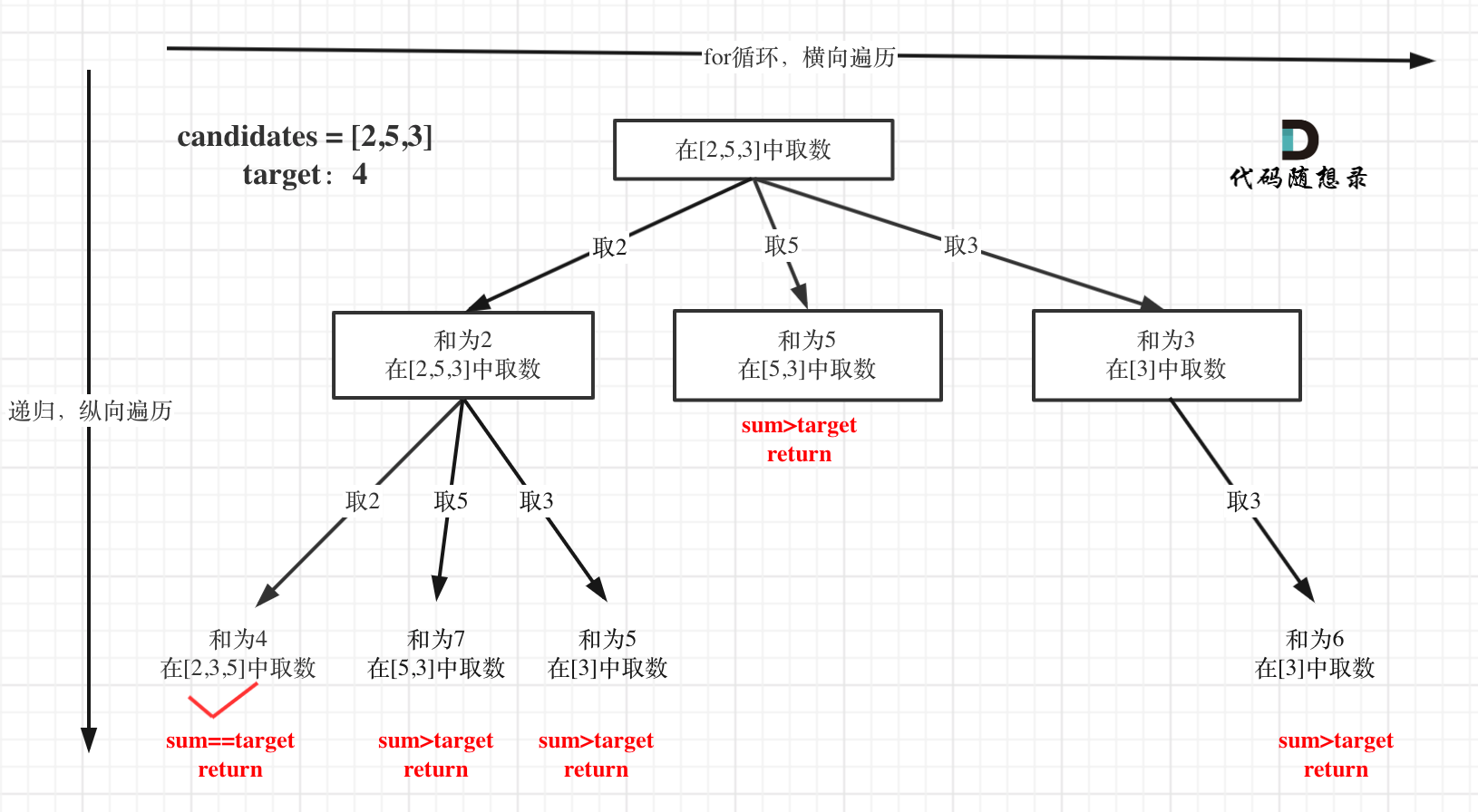
因为所有组合不能重复，所以取完第一层数据以后，第二层并不是继续原始数组。
这里主要是两点我自己没想好就开始写代码的。
1、当sum > target 的时候就应该返回，不然会无限选择。
2、对于组合问题，什么时候需要startIndex呢？
答：如果是求的组合问题，不包含重复元素，就需要每一层起始位置不一样。
这里startIndex应该和第一层取的元素下标一样即可，保证取的组合不重复。（）运行代码
var res [][]intfunc combinationSum(candidates []int, target int) [][]int {res = [][]int{}if len(candidates) == 0 || target < 0{return res}backtracing(0,target,0,candidates,[]int{})return res}func backtracing(start,target,sum int,candidates []int,path []int){if sum == target{temp := make([]int,len(path))copy(temp,path)res = append(res,temp)return}if sum > target{return}for i := start;i < len(candidates);i++{//这里起始位置一定要是start，不可以是0，因为这样才//保证组合不重复sum += candidates[i]path = append(path,candidates[i])backtracing(i,target,sum,candidates,path)sum -= candidates[i]path = path[:len(path)-1]}}
40. 组合总和 II
题目描述
给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意：解集不能包含重复的组合。
思路
一看到这个题，首先确定，求和为target，这时候应该能想到终止条件。
因为不可以含有重复组合，所以递归的时候起始位置为i。每个元素只能使用一次，所以start为 i+1。
元素也不可以重复用，所以就需要对数组进行排序，然后在for循环的时候，同一层不可以有相同元素。运行代码
```go
var res [][]int
func combinationSum2(candidates []int, target int) [][]int {
res = [][]int{}
sort.Ints(candidates)
if len(candidates) == 0 || target < 0{
return res
}
backtracing(0,target,0,candidates,[]int{})
return res
}
func backtracing(start,target,sum int,candidates []int,path []int){
if sum == target{
temp := make([]int,len(path))
copy(temp,path)
res = append(res,temp)
return
}
if sum > target{
return
}
for i := start;i < len(candidates);i++{//这里起始位置一定要是start，不可以是0，因为这样才
//保证组合不重复
if i>start && candidates[i] == candidates[i-1]{
continue
}
sum += candidates[i]
path = append(path,candidates[i])
backtracing(i+1,target,sum,candidates,path)
sum -= candidates[i]
path = path[:len(path)-1]
}
}
<a name="G8BMZ"></a>## [131. 分割回文串](https://leetcode.cn/problems/palindrome-partitioning/)<a name="ufk1Y"></a>### 题目描述给你一个字符串 s，请你将_ _s_ _分割成一些子串，使每个子串都是 **回文串** 。返回 s 所有可能的分割方案。<br />**回文串** 是正着读和反着读都一样的字符串。<br /><a name="q3D9j"></a>### 思路分析一下怎么切割，只看第一层循环，第一次切割找到start：i，也就是0：0，第一个字符，然后第二次找0：2，前两个字符，这样一次类推。这是第一层。假如找到第一个字符，然后开始切割后面的，使用同样的方法，不断找当第一种切割的前提下，其他的切割方法。<br />如下图，第一次切a，下面只能切a，切ab。第二次切aa，下一次切b，第三次切aab。<br />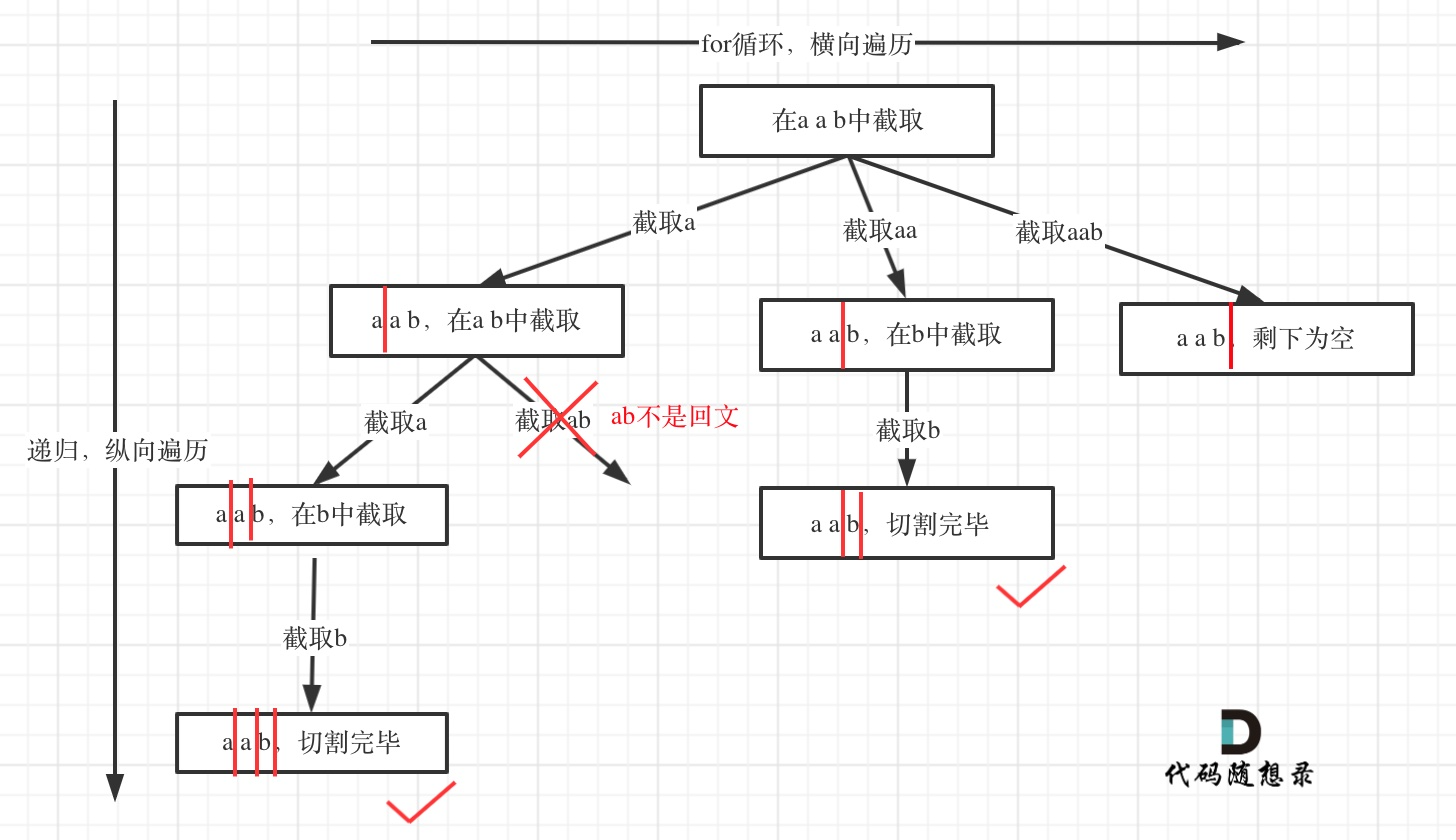<a name="e57dU"></a>### 运行代码```gofunc partition(s string) [][]string {var tmpString []string//切割字符串集合var res [][]string//结果集合backTracking(s,tmpString,0,&res)return res}func backTracking(s string,tmpString []string,startIndex int,res *[][]string){if startIndex==len(s){//到达字符串末尾了//进行一次切片拷贝，怕之后的操作影响tmpString切片内的值t := make([]string, len(tmpString))copy(t, tmpString)*res=append(*res,t)}for i:=startIndex;i<len(s);i++{//处理（首先通过startIndex和i判断切割的区间，进而判断该区间的字符串是否为回文，若为回文，则加入到tmpString，否则继续后移，找到回文区间）（这里为一层处理）if isPartition(s,startIndex,i){tmpString=append(tmpString,s[startIndex:i+1])}else{continue}//递归backTracking(s,tmpString,i+1,res)//回溯tmpString=tmpString[:len(tmpString)-1]}}//判断是否为回文func isPartition(s string,startIndex,end int)bool{left:=startIndexright:=endfor ;left<right;{if s[left]!=s[right]{return false}//移动左右指针left++right--}return true}
93. 复原 IP 地址
题目描述
思路
该题和前一道题分割字符串类似，使用回溯搜索法把所有可能性搜出来。思路图如下：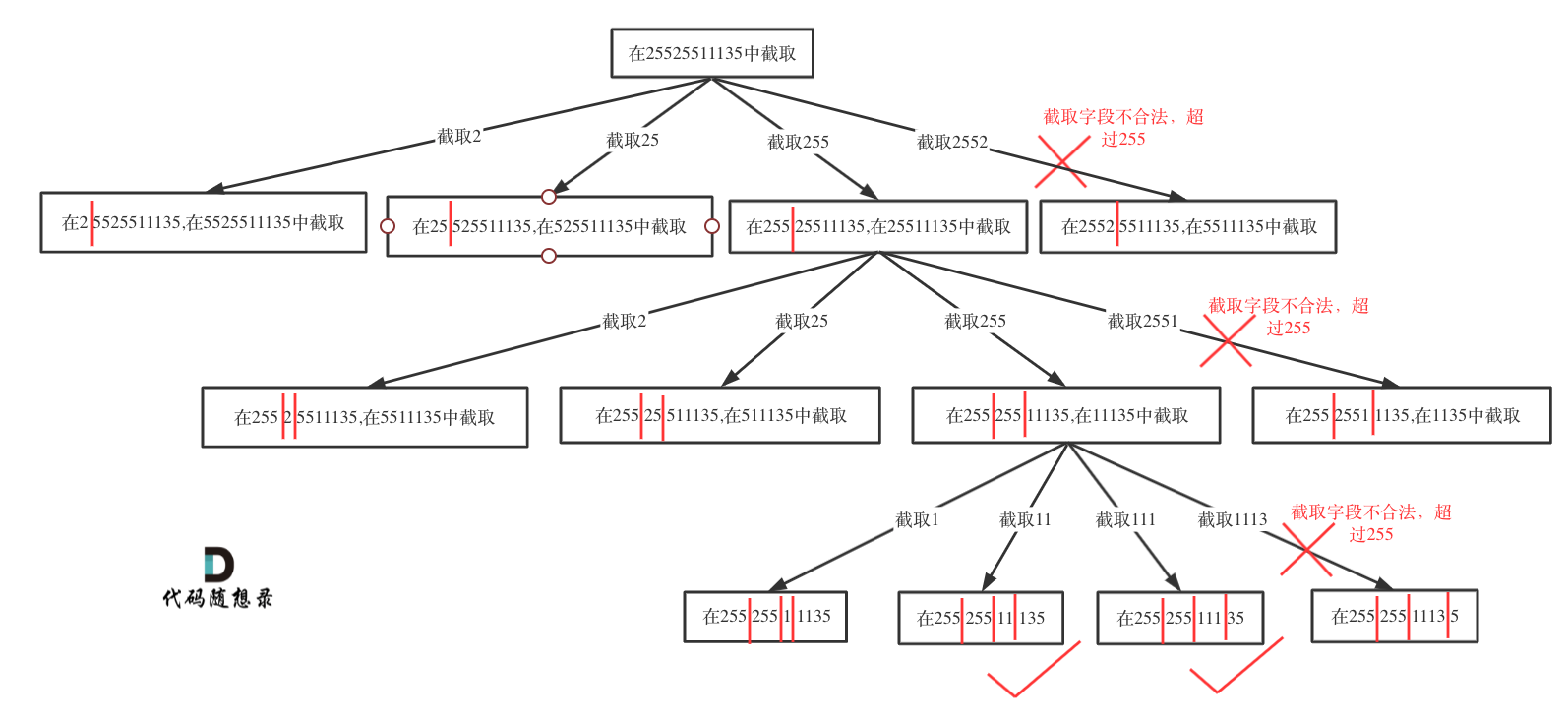
startIndex一定是需要的，因为不能重复分割，记录下一层递归分割的起始位置。
本题我们还需要一个变量pointNum，记录添加逗点的数量。
递归调用时，下一层递归的startIndex要从i+2开始（因为需要在字符串中加入了分隔符.），同时记录分割符的数量pointNum 要 +1。
回溯的时候，就将刚刚加入的分隔符. 删掉就可以了，pointNum也要-1。
运行代码
func restoreIpAddresses(s string) []string {var res,path []stringbackTracking(s,path,0,&res)return res}func backTracking(s string,path []string,startIndex int,res *[]string){//终止条件if startIndex==len(s)&&len(path)==4{tmpIpString:=path[0]+"."+path[1]+"."+path[2]+"."+path[3]*res=append(*res,tmpIpString)}for i:=startIndex;i<len(s);i++{//处理path:=append(path,s[startIndex:i+1])if i-startIndex+1<=3&&len(path)<=4&&isNormalIp(s,startIndex,i){//递归backTracking(s,path,i+1,res)}else {//如果首尾超过了3个，或路径多余4个，或前导为0，或大于255，直接回退return}//回溯path=path[:len(path)-1]}}func isNormalIp(s string,startIndex,end int)bool{checkInt,_:=strconv.Atoi(s[startIndex:end+1])if end-startIndex+1>1&&s[startIndex]=='0'{//对于前导 0的IP（特别注意s[startIndex]=='0'的判断，不应该写成s[startIndex]==0，因为s截取出来不是数字）return false}if checkInt>255{return false}return true}
78. 子集
题目描述
思路
组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点！
其实子集也是一种组合问题，因为它的集合是无序的，子集{1,2} 和 子集{2,1}是一样的。
那么既然是无序，取过的元素不会重复取，写回溯算法的时候，for就要从startIndex开始，而不是从0开始！
以示例中nums = [1,2,3]为例把求子集抽象为树型结构，如下：
本题其实就是把所有的点都遍历，每次取完一个就要往数组中添加。而且重复元素不可以加进去。
运行代码
func subsets(nums []int) [][]int {var res [][]intsort.Ints(nums)backtracking(0,nums,[]int{},&res)return res}func backtracking(start int,nums []int,path []int,res *[][]int){temp := make([]int,len(path))copy(temp,path)*res = append(*res,temp)for i:=start;i<len(nums);i++{if i >0&&nums[i] == nums[i-1]{continue}path = append(path,nums[i])backtracking(i+1,nums,path,res)path = path[:len(path)-1]}}
90. 子集 II
题目描述
思路
这道题目和上一题的区别就是集合里有重复元素了，而且求取的子集要去重。
用示例中的[1, 2, 2] 来举例，如图所示： （注意去重需要先对集合排序）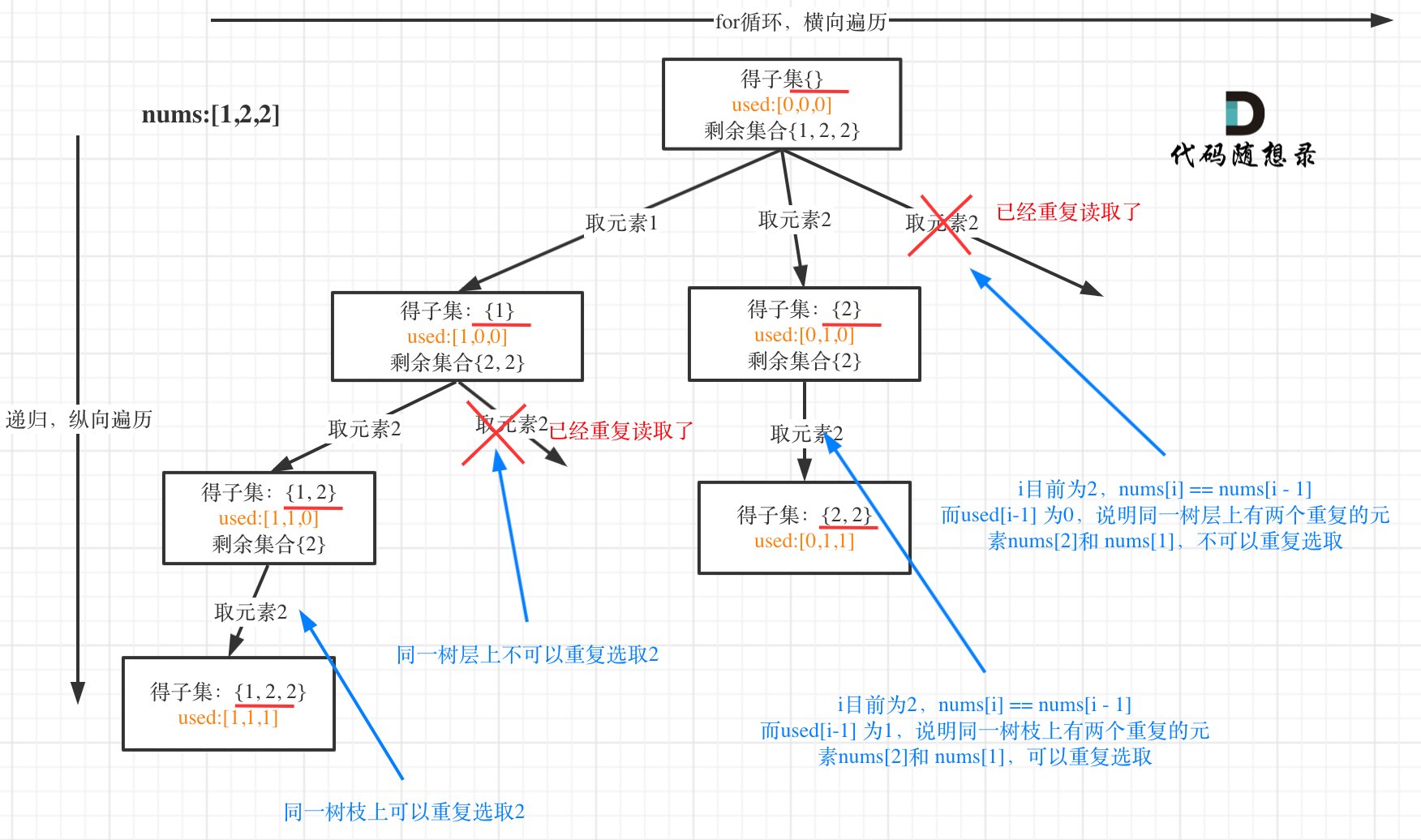
从图中可以看出，同一树层上重复取2 就要过滤掉，同一树枝上就可以重复取2，因为同一树枝上元素的集合才是唯一子集！
运行代码
func subsetsWithDup(nums []int) [][]int {var res [][]intsort.Ints(nums)backtracking(0,nums,[]int{},&res)return res}func backtracking(start int,nums []int,path []int,res *[][]int){temp := make([]int,len(path))copy(temp,path)*res = append(*res,temp)for i:=start;i<len(nums);i++{if i >start&&nums[i] == nums[i-1]{continue}path = append(path,nums[i])backtracking(i+1,nums,path,res)path = path[:len(path)-1]}}
从代码中可以看出，和上一题唯一不同的地方就是第12行，一个是大于0一个是大于start。
大于0：因为i除了第一次为0后面都不为0，也就说明，不管是同一层还是同一个树枝，都不允许后面元素重复。如下图，这里不仅仅在同一层中规定了不允许取元素2不能重复取，还规定了取1取2之后不可以再取下一层的2。这里适用于要求数组中不能包含重复数字。
大于start：只规定了，同一层不可以取相同的元素。
当然，前提都是要对数组进行排序。sort.Ints(nums)
491. 递增子序列
题目描述
思路
而本题求自增子序列，是不能对原数组经行排序的，排完序的数组都是自增子序列了。
所以不能使用之前的去重逻辑！
本题给出的示例，还是一个有序数组 [4, 6, 7, 7]，这更容易误导大家按照排序的思路去做了。
为了有鲜明的对比，我用[4, 7, 6, 7]这个数组来举例，抽象为树形结构如图：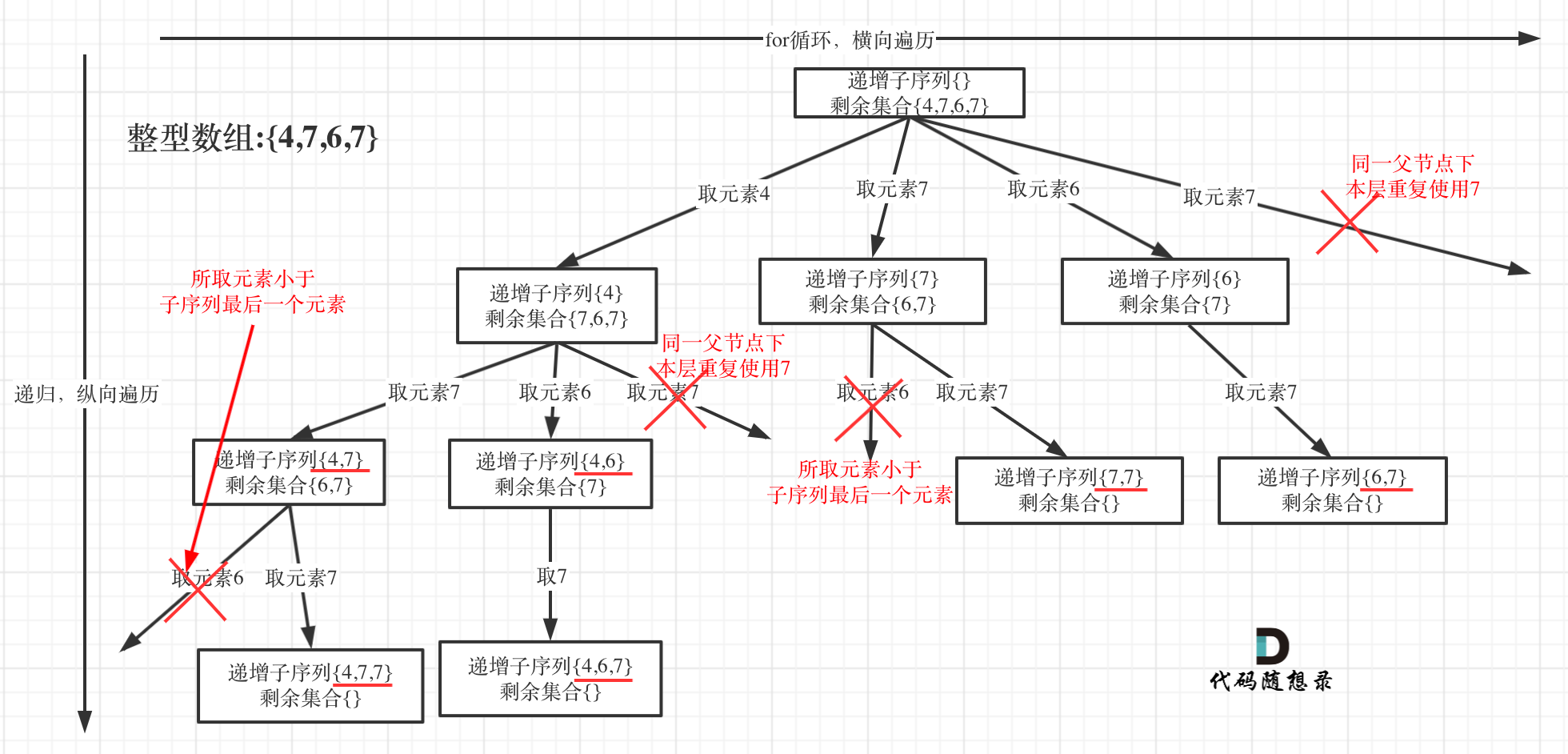
本题求子序列，很明显一个元素不能重复使用，所以需要startIndex，调整下一层递归的起始位置。
- 终止条件
本题其实类似求子集问题，也是要遍历树形结构找每一个节点，所以和回溯算法：求子集问题！(opens new window)一样，可以不加终止条件，startIndex每次都会加1，并不会无限递归。
在图中可以看出，同一父节点下的同层上使用过的元素就不能在使用了，这里因为不可以提前排序，所以不可以用nums[ i ] == nums[ i-1 ]来判断，只能使用哈希表来判断。也就是同一层中相同元素不可以重复选择。
运行代码
func findSubsequences(nums []int) [][]int {var subRes []intvar res [][]intbackTring(0,nums,subRes,&res)return res}func backTring(startIndex int,nums,subRes []int,res *[][]int){if len(subRes)>1{tmp:=make([]int,len(subRes))copy(tmp,subRes)*res=append(*res,tmp)}history:=[201]int{}//记录本层元素使用记录for i:=startIndex;i<len(nums);i++{//分两种情况判断：//一，当前取的元素小于子集的最后一个元素，则继续寻找下一个适合的元素//或者二，当前取的元素在本层已经出现过了，所以跳过该元素，继续寻找if len(subRes)>0&&nums[i]<subRes[len(subRes)-1]||history[nums[i] + 100]==1{continue}history[nums[i] + 100]=1//表示本层该元素使用过了subRes=append(subRes,nums[i])backTring(i+1,nums,subRes,res)subRes=subRes[:len(subRes)-1]}}
46. 全排列
题目描述
思路
排列是有序的，也就是说 [1,2] 和 [2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方。
可以看出元素1在[1,2]中已经使用过了，但是在[2,1]中还要在使用一次1，所以处理排列问题就不用使用startIndex了。
但排列问题需要一个used数组，标记已经选择的元素，如图橘黄色部分所示: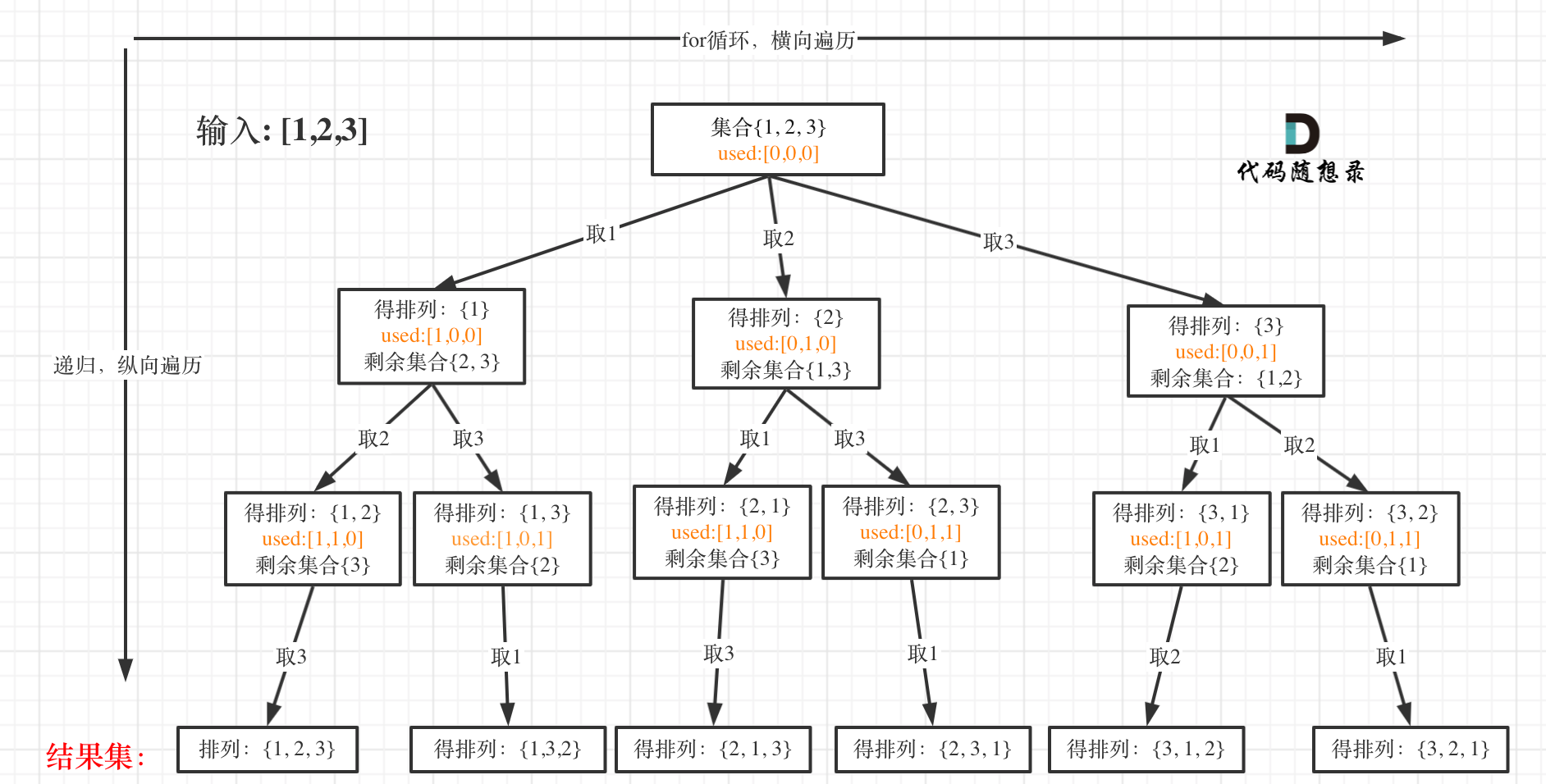
当收集元素的数组path的大小达到和nums数组一样大的时候，说明找到了一个全排列，也表示到达了叶子节点。
而used数组，其实就是记录此时path里都有哪些元素使用了，一个排列里一个元素只能使用一次。
排列问题的不同：
- 每层都是从0开始搜索而不是startIndex
-
运行代码
var res [][]intfunc permute(nums []int) [][]int {res = [][]int{}backTrack(nums,len(nums),[]int{})return res}func backTrack(nums []int,numsLen int,path []int) {if len(nums)==0{p:=make([]int,len(path))copy(p,path)res = append(res,p)}for i:=0;i<numsLen;i++{cur:=nums[i]path = append(path,cur)nums = append(nums[:i],nums[i+1:]...)//直接使用切片backTrack(nums,len(nums),path)nums = append(nums[:i],append([]int{cur},nums[i:]...)...)//回溯的时候切片也要复原，元素位置不能变path = path[:len(path)-1]}}
47. 全排列 II
题目描述
思路
运行代码
```go var res [][]int func permute(nums []int) [][]int { res = [][]int{} backTrack(nums,len(nums),[]int{}) return res } func backTrack(nums []int,numsLen int,path []int) { if len(nums)==0{
p:=make([]int,len(path))copy(p,path)res = append(res,p)
} used := [21]int{}//跟前一题唯一的区别，同一层不使用重复的数。关于used的思想carl在递增子序列那一题中提到过 for i:=0;i<numsLen;i++{
if used[nums[i]+10]==1{continue}cur:=nums[i]path = append(path,cur)used[nums[i]+10]=1nums = append(nums[:i],nums[i+1:]...)backTrack(nums,len(nums),path)nums = append(nums[:i],append([]int{cur},nums[i:]...)...)path = path[:len(path)-1]
}
} ```
若有收获，就点个赞吧
0 人点赞
