golang中list是一个双向链表，第一个 元素是front，最后一个是back

递归遍历

image.png

迭代遍历统一写法

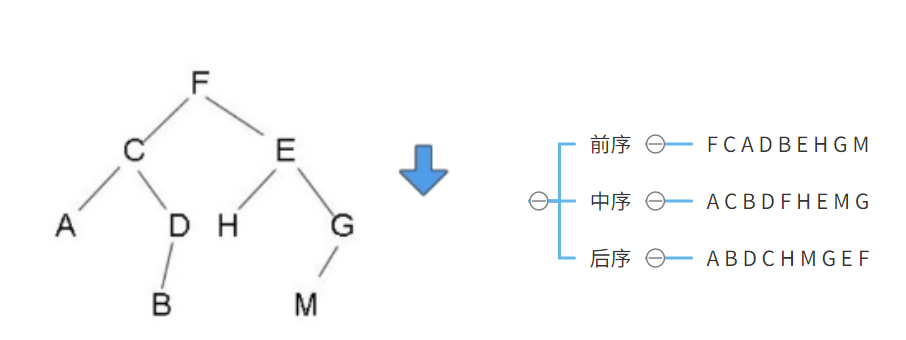
image.png

前序

首先定义一个栈，把FCA依次压入栈中，A没有左子树，所以停止压栈，然后A出栈，A没有右子树，开始C出栈（这时候说明C的所有左子树都被访问完了），查看C是不是有右子树没有就弹出F，有就操作C的右子树，把C的右子树的所有左链压入栈也即B依次这样操作，F有右孩子，然后一样的操作。关于保存值，访问一个新的就保存一个就行了。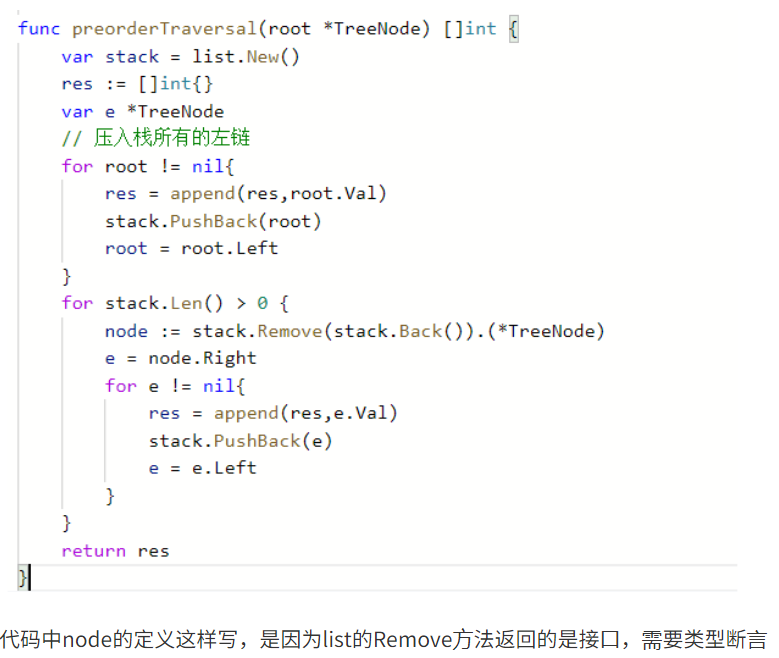
image.png

中序

和前序不同的是，中序遍历顺序正好是前序的出栈顺序，保存出栈的元素即可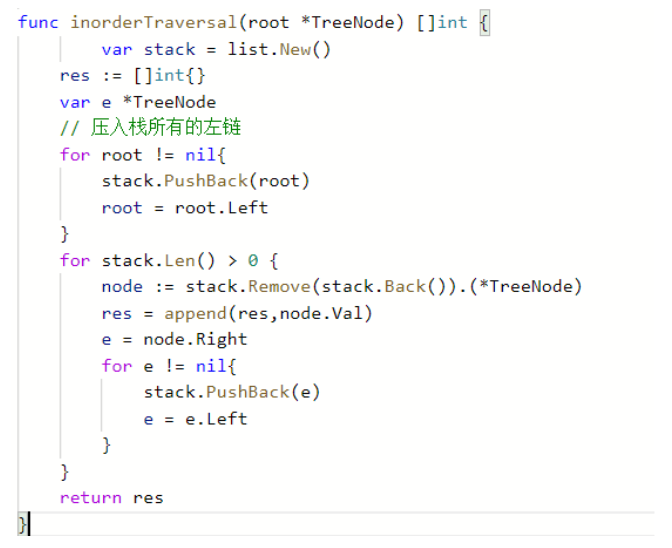
image.png

后序

后续因为是左右根，所有我们可以反转一下，遍历根右左，也就是前序遍历。然后在往res数组放值的时候，最后反转一下res就行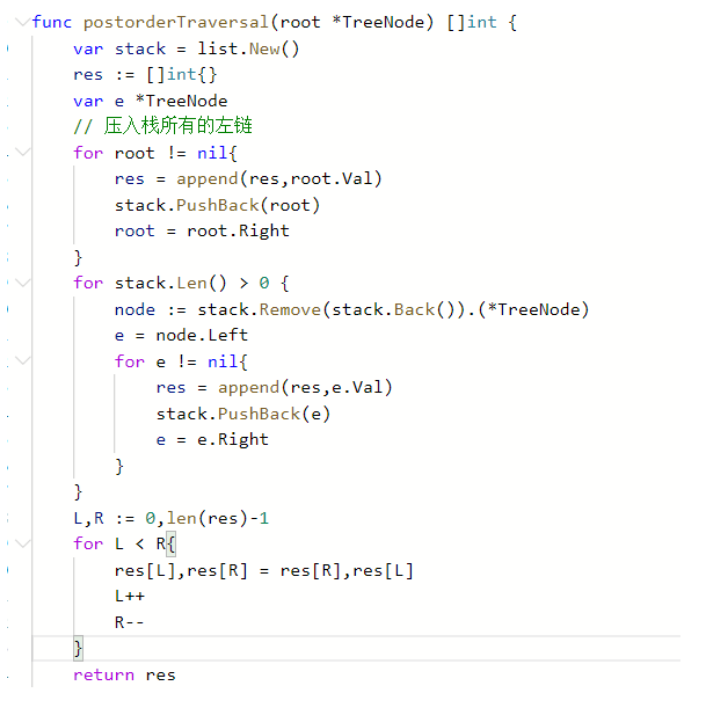
image.png

二叉树的层序遍历

思路：首先定义一个队列，把根节点放进队列中，遍历整个队列，结束标志为空。首先保存一下当前队列长度，为了能够把当前层的所有元素遍历完，每遍历一个节点，就放进队列一个，然后再添加它的左右孩子节点，这时候的添加则是属于下一层的元素
下面这个是错的

  1. /**
  2.  * Definition for a binary tree node.
  3.  * type TreeNode struct {
  4.  *     Val int
  5.  *     Left *TreeNode
  6.  *     Right *TreeNode
  7.  * }
  8.  */
  9. func levelOrder(root *TreeNode) [][]int {
  10.     res := [][]int{}
  11.     if root==nil{//防止为空
  12.         return res
  13.     }
  14.     temp := []int{}
  15.     queue := list.New()
  16.     queue.PushBack(root)
  17.     for queue.Len() > 0 {
  18.         for i := 0;i < queue.Len();i++{//这里是错的，因为queue.Len()是不断动态变化的
  19.             node := queue.Remove(queue.Back()).(*TreeNode)//这里不可说是Back，而是Front。因为list是双向链表
  20.             if node.Left != nil{
  21.                 queue.PushBack(node.Left)
  22.             }
  23.             if node.Right != nil{
  24.                 queue.PushBack(node.Right)
  25.             }
  26.             temp = append(temp,node.Val)
  27.         }
  28.         res = append(res,temp)
  29.         temp = []int{}
  30.     }
  31.     return res
  32. }
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func levelOrder(root *TreeNode) [][]int {
    res := [][]int{}
    if root==nil{//防止为空
        return res
    }
    temp := []int{}
    queue := list.New()
    queue.PushBack(root)
    for queue.Len() > 0 {
        length := queue.Len()
        for i := 0;i < length;i++{
            node:=queue.Remove(queue.Front()).(*TreeNode)
            if node.Left != nil{
                queue.PushBack(node.Left)
            }
            if node.Right != nil{
                queue.PushBack(node.Right)
            }
            temp = append(temp,node.Val)
        }
        res = append(res,temp)
        temp = []int{}
    }
    return res
}

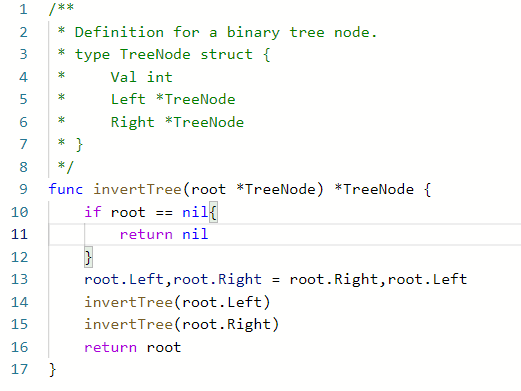
翻转二叉树

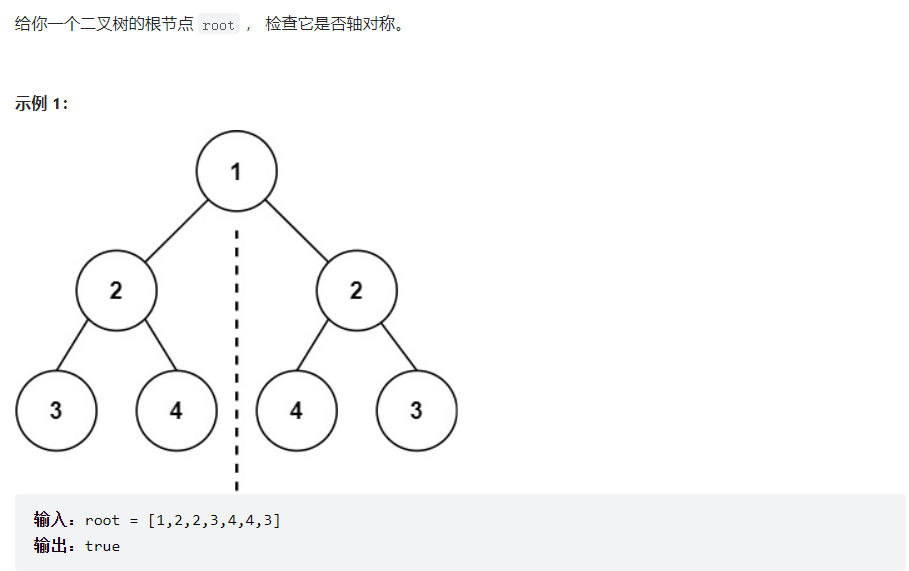
image.png

对称二叉树

image.png

func isSymmetric(root *TreeNode) bool {
    var queue []*TreeNode;
    if root != nil {
        queue = append(queue, root.Left, root.Right)
    }//首先把左右子树放到数组里面
    for len(queue) > 0 {
        left := queue[0]
        right := queue[1]//每次取数组的前两个值
        queue = queue[2:]//取完两个值以后去掉这两个值
        if left == nil && right == nil {
            continue
        }
        if left == nil || right == nil || left.Val != right.Val {
            return false
        }
        //上面两个值比较完以后，开始把左子树的左节点，右子树的右节点，右子树的左节点，左子树的右节点
        //放到数组里
        queue = append(queue, left.Left, right.Right, right.Left, left.Right)
    }
    return true
}

二叉树最大深度

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func maxDepth(root *TreeNode) int {
    queue:=list.New()
    max := 0
    if root==nil{
        return 0
    }
    queue.PushBack(root)
    for queue.Len()>0{
        length:=queue.Len()
        for i:=0;i<length;i++{
            node:=queue.Remove(queue.Front()).(*TreeNode)
            if node.Left!=nil{
                queue.PushBack(node.Left)
            }
            if node.Right!=nil{
                queue.PushBack(node.Right)
            }

        }
        max++
    }
    return max
}

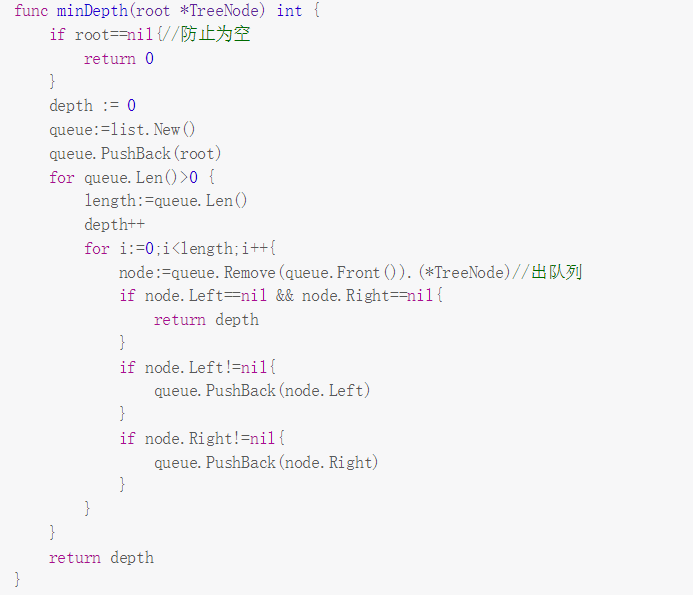
二叉树最小深度

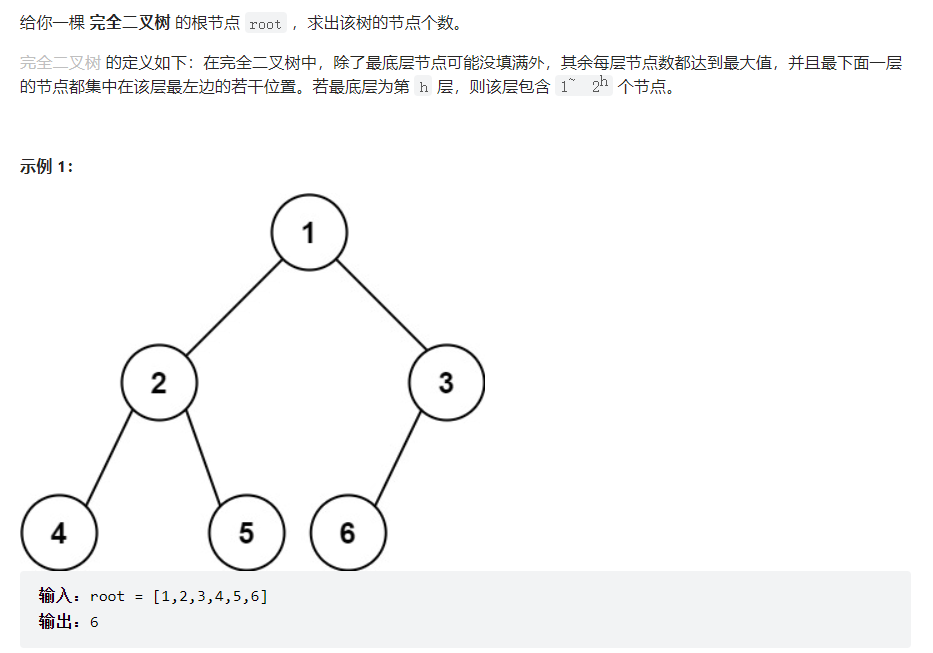
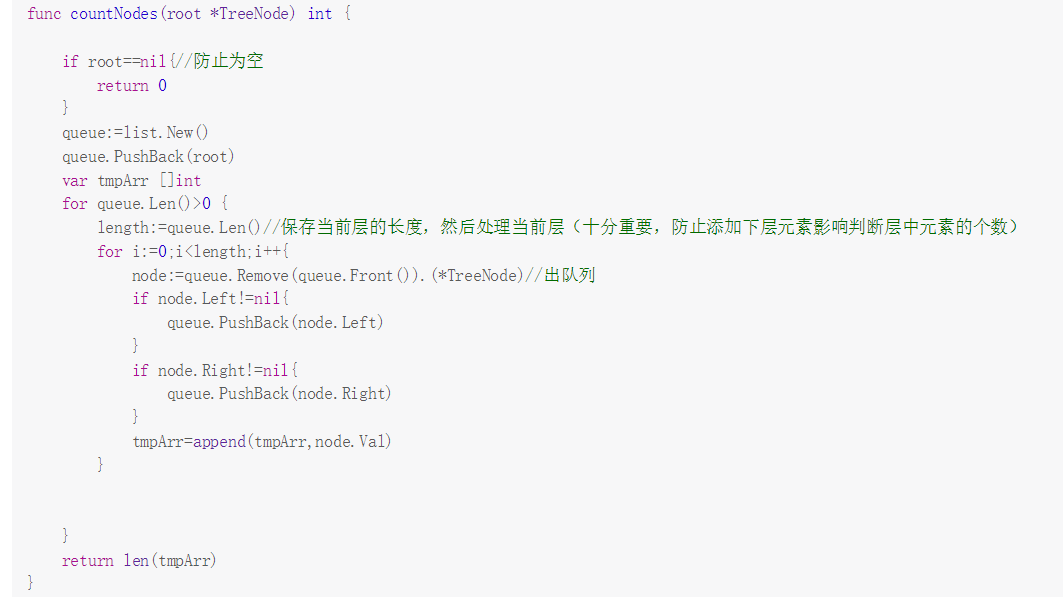
image.png

完全二叉树节点个数

image.png
image.png

平衡二叉树（没有写）

二叉树的所有路径

func binaryTreePaths(root *TreeNode) []string {
    res := make([]string, 0)
    var travel func(node *TreeNode, s string)
    travel = func(node *TreeNode, s string) {
        if node.Left == nil && node.Right == nil {
            v := s + strconv.Itoa(node.Val)
            res = append(res, v)
            return
        }
        s = s + strconv.Itoa(node.Val) + "->"
        if node.Left != nil {
            travel(node.Left, s)
        }
        if node.Right != nil {
            travel(node.Right, s)
        }
    }
    travel(root, "")
    return res
}

找树左下角的值

image.png