二叉树

二叉树（Binary Tree）顾名思义，每个节点最多有两个“叉”，也就是两个子节点，分别是左子节点和右子节点。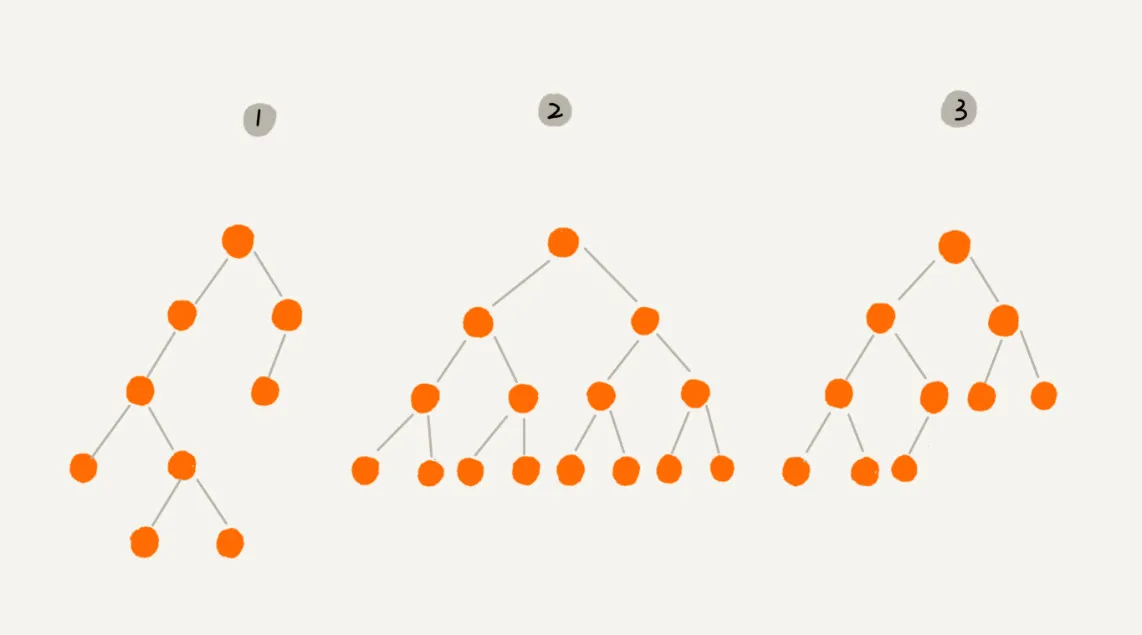
image.png
2号树为满二叉树：叶子节点全都在最底层，除了叶子节点之外，每个节点都有左右两个子节点。
3号树为完全二叉树：叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大。

链式存储法：使用链表存储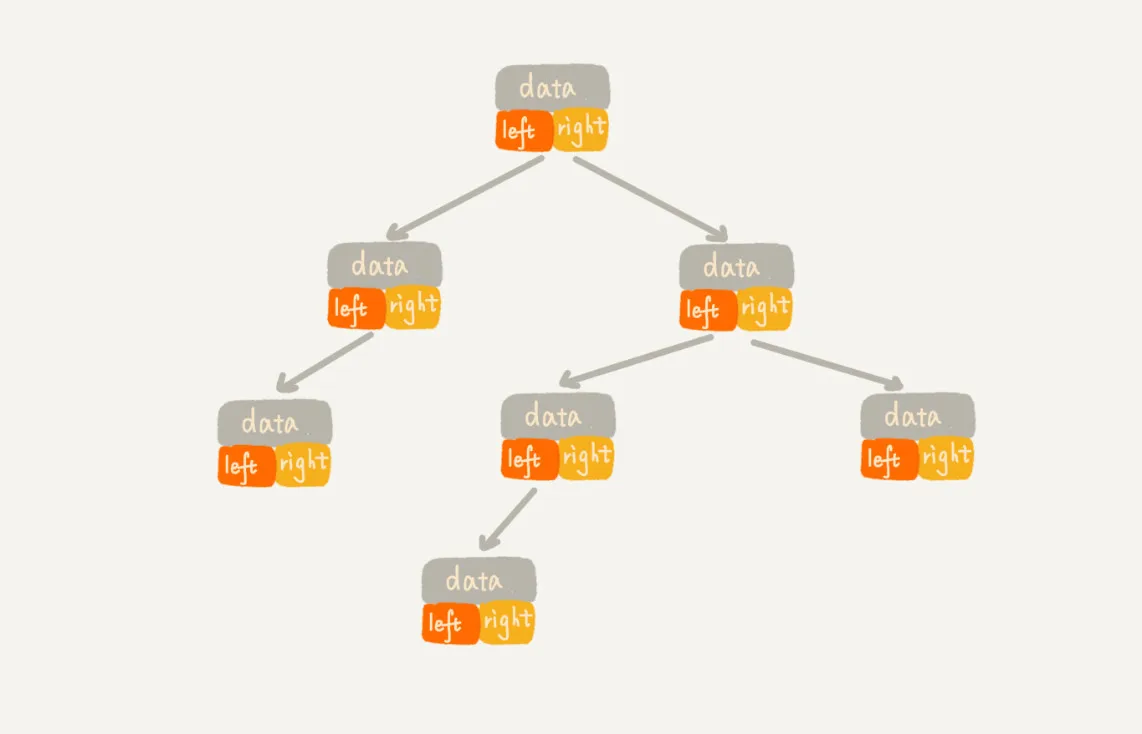
image.png

顺序存储法：使用数组存储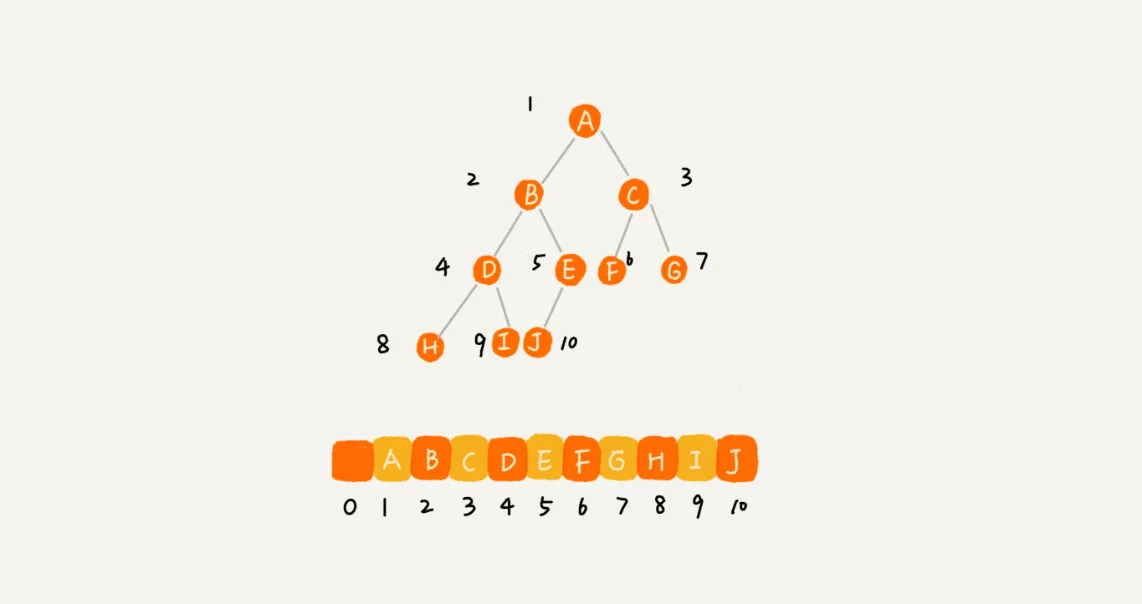
image.png

完全二叉树适合使用顺序存储。

遍历二叉树

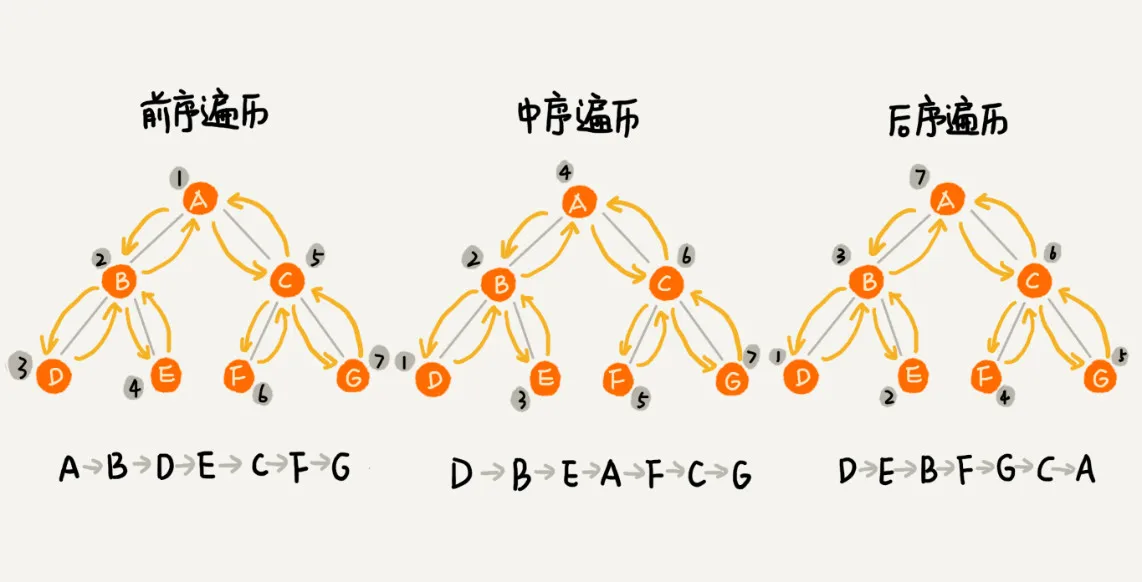
image.png
前序遍历是指，对于树中的任意节点来说，先打印这个节点，然后再打印它的左子树，最后打印它的右子树。
中序遍历是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它本身，最后打印它的右子树。
后序遍历是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它的右子树，最后打印这个节点本身。

中序遍历二叉查找树，可以输出有序的数据序列，时间复杂度是 O(n)，非常高效。

递归遍历：

  1.   private void foreachNode(TreeNode node) {
  2.     if (node == null) {
  3.       return;
  4.     }
  5.     pre.add(node.val); // 前序遍历结果
  6.     foreachNode(node.left);
  7.     mid.add(node.val); // 中序遍历结果
  8.     foreachNode(node.right);
  9.     post.add(node.val); // 后续遍历结果
  10.   }

非递归遍历：

操作二叉树

查找

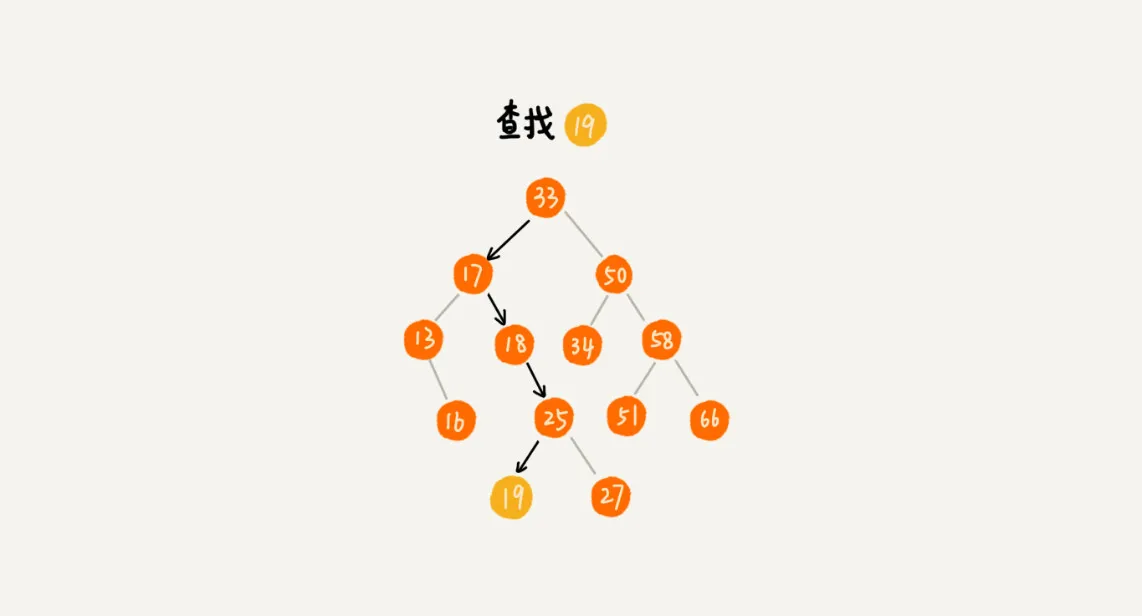
image.png

  2. public class BinarySearchTree {
  3.   private Node tree;
  5.   public Node find(int data) {
  6.     Node p = tree;
  7.     while (p != null) {
  8.       if (data < p.data) p = p.left;
  9.       else if (data > p.data) p = p.right;
  10.       else return p;
  11.     }
  12.     return null;
  13.   }
  15.   public static class Node {
  16.     private int data;
  17.     private Node left;
  18.     private Node right;
  20.     public Node(int data) {
  21.       this.data = data;
  22.     }
  23.   }
  24. }

插入

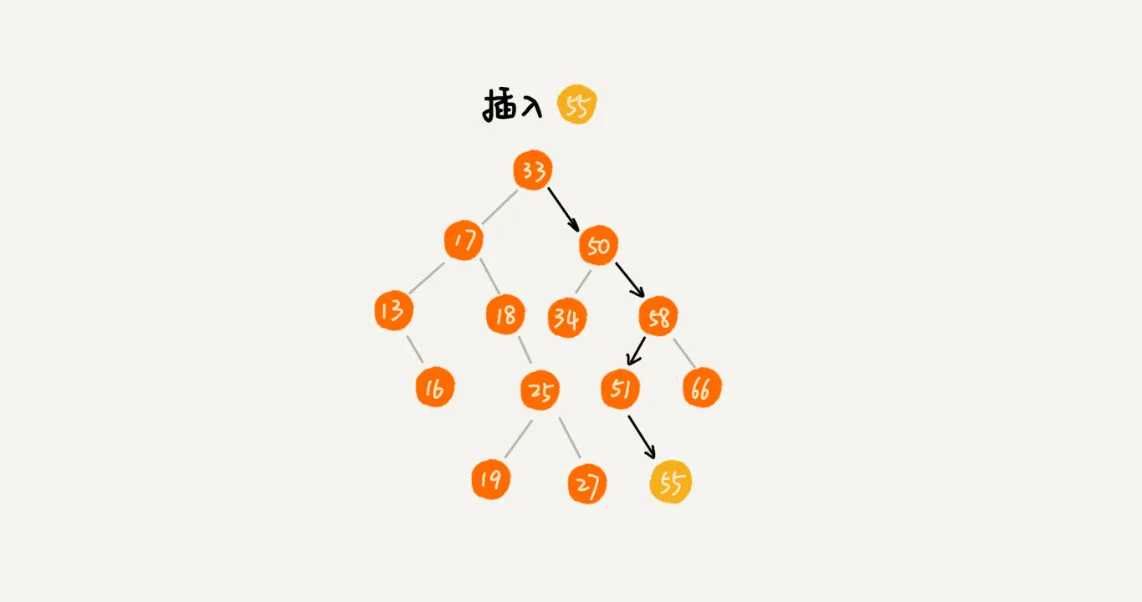
image.png

  1. public void insert(int data) {
  2.   if (tree == null) {
  3.     tree = new Node(data);
  4.     return;
  5.   }
  7.   Node p = tree;
  8.   while (p != null) {
  9.     if (data > p.data) {
  10.       if (p.right == null) {
  11.         p.right = new Node(data);
  12.         return;
  13.       }
  14.       p = p.right;
  15.     } else { // data < p.data
  16.       if (p.left == null) {
  17.         p.left = new Node(data);
  18.         return;
  19.       }
  20.       p = p.left;
  21.     }
  22.   }
  23. }

删除

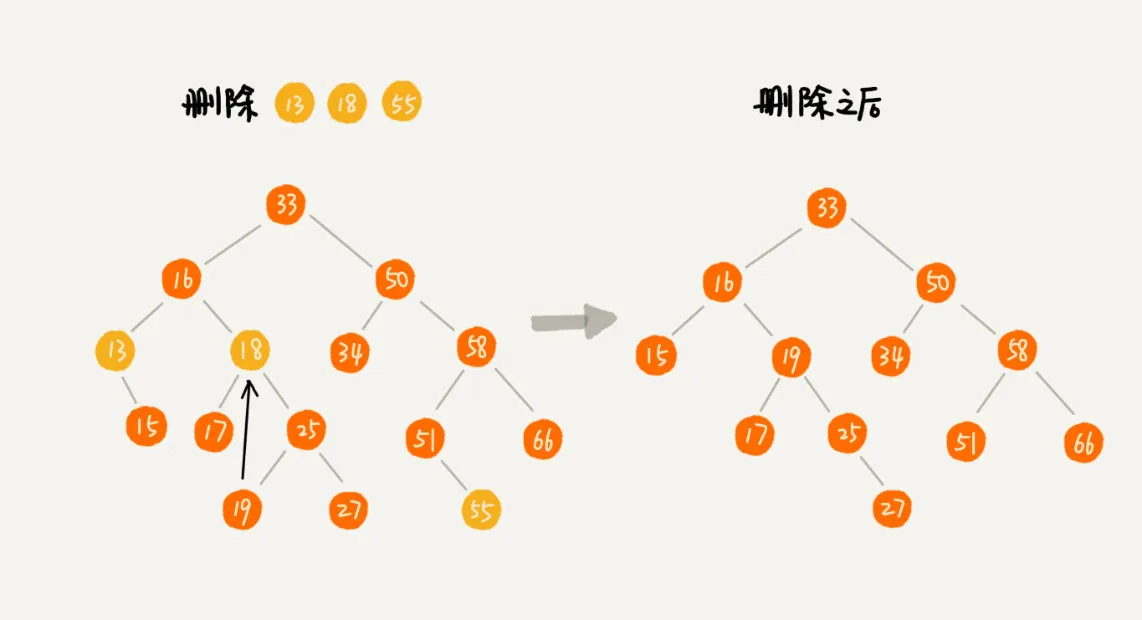
第一种情况是，如果要删除的节点没有子节点，我们只需要直接将父节点中，指向要删除节点的指针置为 null。比如图中的删除节点 55。

第二种情况是，如果要删除的节点只有一个子节点（只有左子节点或者右子节点），我们只需要更新父节点中，指向要删除节点的指针，让它指向要删除节点的子节点就可以了。比如图中的删除节点 13。

第三种情况是，如果要删除的节点有两个子节点，这就比较复杂了。我们需要找到这个节点的右子树中的最小节点，把它替换到要删除的节点上。然后再删除掉这个最小节点，因为最小节点肯定没有左子节点（如果有左子结点，那就不是最小节点了），所以，我们可以应用上面两条规则来删除这个最小节点。比如图中的删除节点 18。

image.png

  2. public void delete(int data) {
  3.   Node p = tree; // p指向要删除的节点，初始化指向根节点
  4.   Node pp = null; // pp记录的是p的父节点
  5.   while (p != null && p.data != data) {
  6.     pp = p;
  7.     if (data > p.data) p = p.right;
  8.     else p = p.left;
  9.   }
  10.   if (p == null) return; // 没有找到
  12.   // 要删除的节点有两个子节点
  13.   if (p.left != null && p.right != null) { // 查找右子树中最小节点
  14.     Node minP = p.right;
  15.     Node minPP = p; // minPP表示minP的父节点
  16.     while (minP.left != null) {
  17.       minPP = minP;
  18.       minP = minP.left;
  19.     }
  20.     p.data = minP.data; // 将minP的数据替换到p中
  21.     p = minP; // 下面就变成了删除minP了
  22.     pp = minPP;
  23.   }
  25.   // 删除节点是叶子节点或者仅有一个子节点
  26.   Node child; // p的子节点
  27.   if (p.left != null) child = p.left;
  28.   else if (p.right != null) child = p.right;
  29.   else child = null;
  31.   if (pp == null) tree = child; // 删除的是根节点
  32.   else if (pp.left == p) pp.left = child;
  33.   else pp.right = child;
  34. }

实际上，关于二叉查找树的删除操作，还有个非常简单、取巧的方法，就是单纯将要删除的节点标记为“已删除”，但是并不真正从树中将这个节点去掉。这样原本删除的节点还需要存储在内存中，比较浪费内存空间，但是删除操作就变得简单了很多。而且，这种处理方法也并没有增加插入、查找操作代码实现的难度。

快速查找最大节点
快速查找最小节点
快速查找前驱节点
快速查找后继节点

支持重复数据的二叉树

第一种方法比较容易。二叉查找树中每一个节点不仅会存储一个数据，因此我们通过链表和支持动态扩容的数组等数据结构，把值相同的数据都存储在同一个节点上。

第二种方法比较不好理解，不过更加优雅。每个节点仍然只存储一个数据。在查找插入位置的过程中，如果碰到一个节点的值，与要插入数据的值相同，我们就将这个要插入的数据放到这个节点的右子树，也就是说，把这个新插入的数据当作大于这个节点的值来处理。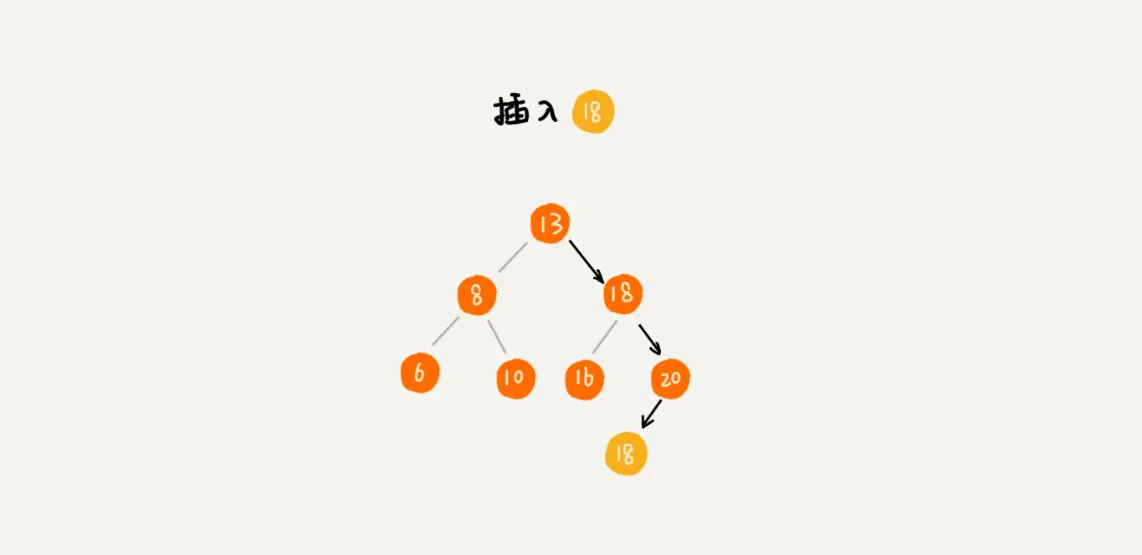
image.png
当要查找数据的时候，遇到值相同的节点，我们并不停止查找操作，而是继续在右子树中查找，直到遇到叶子节点，才停止。这样就可以把键值等于要查找值的所有节点都找出来。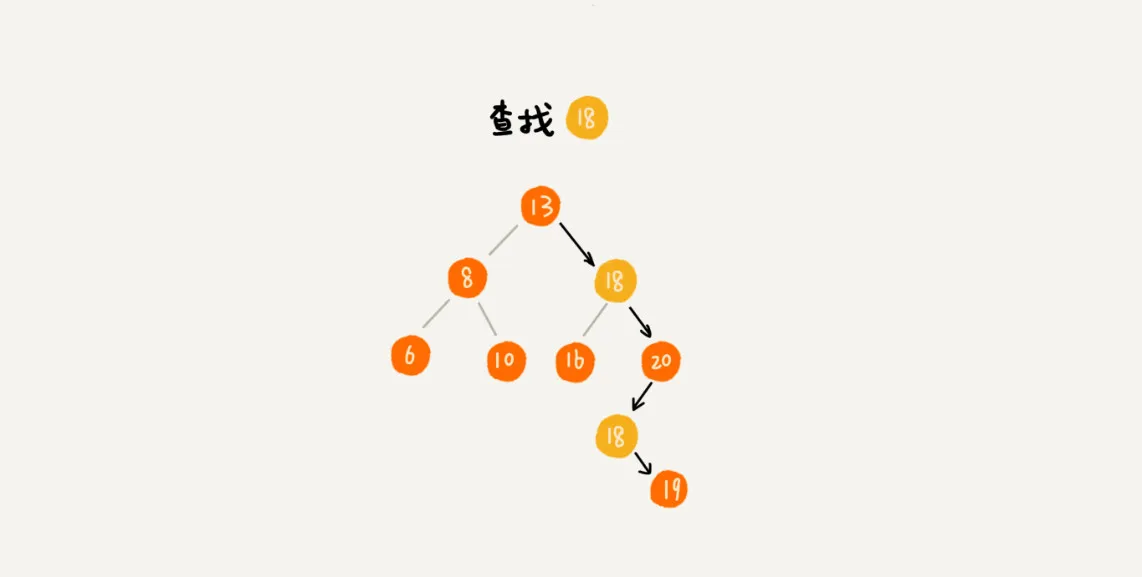
image.png
对于删除操作，我们也需要先查找到每个要删除的节点，然后再按前面讲的删除操作的方法，依次删除。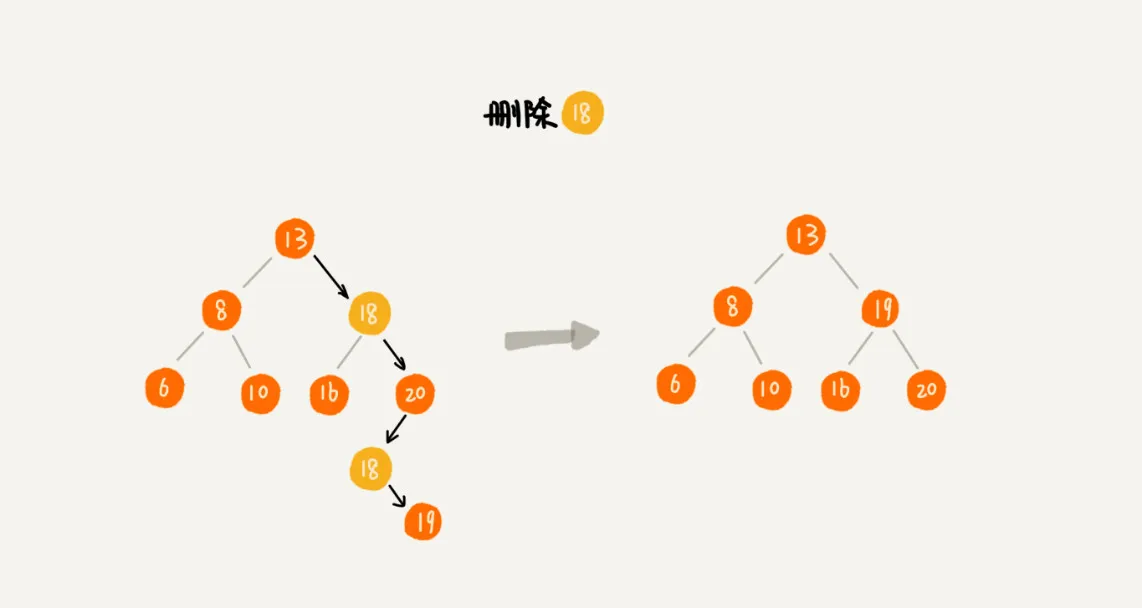
image.png

二叉树查找时间复杂度

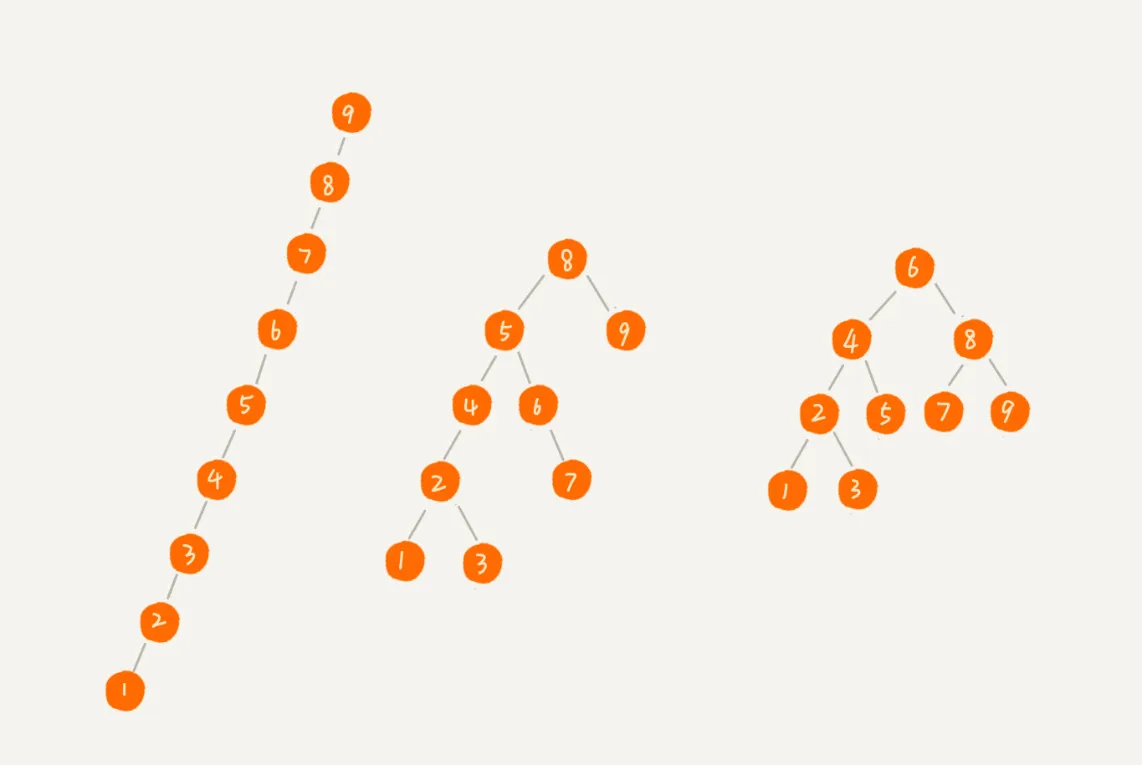
image.png
最坏情况时间复杂度：二叉树退化为链表时为O(n)
理想情况时间复杂度：满二叉树或完全二叉树，时间复杂度与树高成正比，为O(logn)。

二叉树的优势

中序遍历，可以在 O(n) 的时间复杂度内，输出有序的数据序列。