陈希儒院士的统计学入门书，上一版本为清华大学出版社的版本，豆瓣9.3分。2021年底版本，评分不足。陈希孺先生的统计学数据内容无可挑剔，需要注意的就是阅读的顺序和深度的控制。本书可以作为专业统计学入门的。本书售价69.8，对比2000年版本的15元。每年涨幅为：%22%20aria-hidden%3D%22true%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ2-221A%22%20x%3D%220%22%20y%3D%22-24%22%3E%3C%2Fuse%3E%0A%3Crect%20stroke%3D%22none%22%20width%3D%223281%22%20height%3D%2260%22%20x%3D%221000%22%20y%3D%221067%22%3E%3C%2Frect%3E%0A%3Cg%20transform%3D%22translate(1000%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-36%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-39%22%20x%3D%22500%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2E%22%20x%3D%221001%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-38%22%20x%3D%221279%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2F%22%20x%3D%221780%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(2280%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-35%22%20x%3D%22500%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=%5Csqrt%5B21%5D%7B69.8%2F15%7D%20-1%3D%200.0706&id=v8NtR) :::info 对偶然性的认识，是一个现代人知识结构中应具备的成分，是一个人的人文素质的一部分。正如英国学者威尔斯所说：“统计的思维方法，就像读和写的能力一样，将来有一天会成为效率公民的必备能力。” :::

01 概率 - 机会大小的度量

这本书其实是关于机会的数学，包括数学中的两个学科分支：概率论和数理统计学。大体上说，前者属于机会数量化的理论基础，而后者则是其应用。个人感受而言，学术的可以称为【随机】，通俗的更喜欢【机会】或者【运气】。但在正文中，本版本以【机遇】为主旨，与标题也有区别，比较难受。在笔记中，统一以随机和机会进行指代。

1.1 古典概率

基于试验结果的等可能性，用以下公式规定的概率，叫作“古典概率”：

概率论与梳理统计

:::info 概率论：【随机（机会）】的数量化理论基础
数理统计：【随机（机会）】的应用 :::

排列与组合

排列和组合。它们的区别是：排列要讲究次序，而组合则不需要。举例来说明，有4个相异的物件，分别用A、B、C、D来记。从这4个物件中取出2个来排列，不同的做法有：AB,BA,AC,CA,AD,DA,BC,CB,BD,DB,CD,DC，共计 12 种。若是取出 2 个来组合，则不同的做法只有AB,AC,AD,BC,BD,CD，共计6种。

举一个形象的例子：某个中学要从 4 位教员中挑选 2 位，分别担任校长和副校长，则挑选的方法有 12 种，因为此处次序很重要。相反，若从 4 位乒乓球运动员中挑选 2 位参加双打，则挑选方法只有 6 种，因为在此次序没有意义。

排列的计算，为每次选择的可选项，即可能性的数量的连乘。设定有n个相异的物件，从其中取出r个进行排列：

以上面例子计算：

组合的计算，则是在排列的基础上，再除以选出数量的阶乘。即不同排列，相同组合的数量。比如AB，BA是相同的，所以要除以2的阶乘。

以上面例子计算：

1.2 大数定律

模型

比率是一个极普通但是又极常用而重要的概念，在科技、生产和经济、社会乃至日常生活中，几乎是无所不在的。我们说对一个情况有数量上的掌握，往往就是指对有关比率有较确切的了解。比如说“某厂产品的合格率很高”，高到什么程度？还是不清楚，远不如给出一个具体的合格品率更说明问题。要考察一国或一地区的文盲情况，首要的指标是文盲率——文盲数目占全部人口数目的比率。当然还有文盲的年龄、地域和性别等方面的分布问题，但比率能给出一个总的概念。

因此，在现实生活中，有许多努力就花在搞清楚形形色色的比率上，在许多情况下这是一个需要花费大量人力、物力和时间的工作。如果从理论角度看，则不过是一个“盒子里有两种颜色的球”的模型。例如，对于某工厂的产品，白球代表不合格品而黑球代表合格品；对于文盲率问题，白球代表文盲而黑球代表非文盲，等等。无论问题的实际情况是何等复杂，若问题只涉及比率，就不影响这个模型的代表性。

数学里研究的形形色色的模型、运算、关系等，都是高度抽象的。但这种抽象根植于现实，并非凭空的想象。所谓模型，不过是把一大类本质一样但外表各异的问题，表述成一种规格化的模式而已，它虽是一种抽象，但有丰富的实际内涵，【盒子模型】就是一个极好的例子。

鱼塘问题

我们回到盒子模型，以 ω 和 b 记白球数和黑球数。则黑、白两种球个数之和为 ω+b。接下来用这个模型解决一个实际问题： :::info 鱼塘问题：

1. 鱼塘中有某种鱼，但不知总数 N。
2. 为估计这个数目，从湖中捉上来该种鱼若干条，数目记为 ω。
3. 在这 ω 条鱼上标上记号再放回湖中，等待相当长一段时间，以便使鱼能随机地在湖中散开（这相当于把盒中的球充分扰乱），然后从湖中捞起 n。
4. 其中有记号的有 m 条。

解答：

1. 利用已知的数 ω、n 和 m，就可以对总数 N 做一个估计，方法如下：
   1. ω/N 代表整个湖中该种鱼上有记号者的比率。
   2. 而 m/n 代表捞起的那些鱼中有记号者的比率。近似地视二者为相等，即 ω/N=m/n。
   3. 得 N=nω/m 当然，这只是一种近似的估计而非严格相等。n愈大，误差一般就愈小。 :::

      自助法

      概率要解决的实际问题（其实这是数理统计的范畴，即把概率反向应用的方法）就是要估计出。如果不知道盒子里的具体情况，那么如何估计呢，这里使用到了【自助法 Bootstrap】Bootstrap本来是指靴子后帮上面那个皮质拉环，在统计学中也翻译为为自展法。

这种方法是在抽屉中抽取一个小球并记录颜色之后，再将小球放回的方法。也就是说在下一次抽取时，上面的 ω 和 b 的数量是完全一致的。即各次抽球成为一个【完全同一】试验的重复。完全同一表示每次抽球时条件完全一样，即从有 ω+b 个球的盒中随机抽出一个来。这里书中有些跳，介绍了【伯努利模型】，后续会介绍，为了便于理解可以跳过。

大数定律

伯努利是第一个对大数定律进行描述的人。即根据上面的例子的设定，当试验次数 n 愈来愈大时，【频率】会愈来愈接近比率。也就是说使用自助法进行有放回的抽样，当抽样数量越多时得到的推断越接近实际概率值。

从现实世界的角度看，大数定律是无法严格证明的。说到底，从现实世界的角度看，大数定律是人类观察到的一个经验规律。伯努利大数定律（及其他形形色色的大数定律）的意义，在于对这样一个经验规律给了一个理论上的解释。

1.3 统计概率

频率与概率

设观察了 n 次而事件A出现了 m 次，m/n 称为事件 A 的【频率】。我们相信，当 n 愈来愈大时，频率 m/n 虽有些摆动，但幅度愈来愈小而最终会“趋近”于某一介于0与1之间的值 p，我们就把这个 p定义为事件A的【概率】。在这个定义中，无须有“同等可能”的条件，但要求该事件可以在同样条件下重复观察，这是一个关键。用这种方式定义的概率叫作【统计概率】，因为它是通过“统计”（即进行观察）去定义概率的。

在古典概率的场合，事件概率有一个不依赖于频率的定义——它根本不用诉诸试验，这样才有一个频率与概率是否接近的问题，对这个问题的研究导致了伯努利大数定律。

1.4 主观概率

当事件可以在同样条件下多次重复观察时，该事件的概率可由其出现的频率去决定，虽然它不是确值而只是一个估计，且不同的人通过重复观察所得频率也会有差异。但重要的是，大家公认这是一个客观的合理的方法。不同的人可能得出不同的估计，是偶然性的作用所致，而不是方法上的问题，何况在观察次数足够多时，不同估计之间的差异会很小，以致在应用上不具有重要性。

在一次性事件的场合，频率的方法不能用。到目前为止，还不存在一种得到公认的客观方法去计算其概率，因此只能诉诸主观判断。例如投资一个项目盈利的概率，不同的人的估计可以有很大的出入，这与各人的看法和倾向有关，尤其是，与其掌握的信息资料有关。

这种基于主观判断定出的概率，叫作“主观概率”。有这么一个生动的例子，1999年1月14日的《科学时报》对“神农架是否存在野人”问题的讨论做了报道。这当然是一个一次性事件，因为普天下并无第二个神农架。从报道上看，学者们的意见基本一致，即可能性很小。但意见一致之下仍有些不同，有的学者认为完全不可能，即把“神农架存在野人”这个事件的概率判为 0，另一位学者将其判为 0.05，还有的学者只判断“很小”但未给出数值。这就是各学者对这一事件发生所判的主观概率。【主观概率】是认识主体根据其所掌握的知识、信息和证据，而对某种情况出现可能性大小所做的数量判断。

是否运用主观概率，引起了20世纪发展的【贝叶斯学派】与【频率学派】之争，后续进行详细介绍。

概率分布

上表给出了 x 可能取的值及其相应的概率，称为 x 的“概率分布”。概率分布是随机变量的最完整的描述。概率分布中“分布”一词，指明全部概率是如何分布在随机变量 x 的各个可能值上的。其实上面部分描述的【离散变量】的分布，下面使用【概率密度曲线】的则是【连续变量】的分布。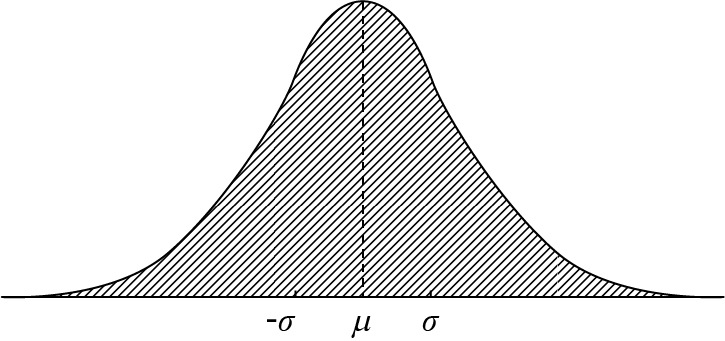

曲线的形式多种多样。形式过于复杂的，在应用上不便。有几种形式较简单的曲线在实际问题中很常用，其中最重要的一种叫作“正态曲线”，又常称为“高斯曲线”，其所代表的概率分布，就称为正态分布或高斯分布。