有段时间没有接触并查集了，但是看了一下代码还是能够快速的看懂，整理一下。
    并查集中最主要的两个方法就是连接两个集合（unionElements），前提是两个集合不是同一个集合（isConnected）也就是集合的根节点（find）不相同。

    1. public interface UF {
    2.     int getSize();
    3.     boolean isConnected(int p, int q);
    4.     void unionElements(int p, int q);
    5.     int  find(int p);
    6. }
    • implementation1

    所有的节点都指向根节点，维护一个数组，数组元素值代表节点的根节点编号。合并两个集合就是把一个集合所有的节点都指向另外一个集合的根节点。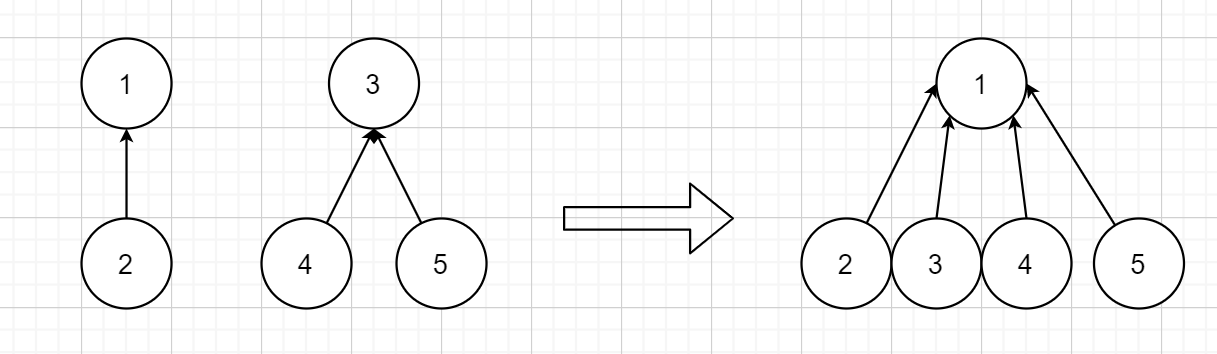
    image.png

    1. public class UnionFind_v1 implements UF{
    3.     private int[] id;
    5.     public UnionFind_v1(int size) {
    7.         id = new int[size];
    9.         for(int i = 0; i < id.length; i++) {
    10.             id[i] = i;
    11.         }
    12.     }
    15.     @Override
    16.     public int getSize() {
    17.         return id.length;
    18.     }
    20.     /**
    21.      * 查看两个元素是否在同一个集合
    22.      * @param p
    23.      * @param q
    24.      * @return
    25.      */
    26.     @Override
    27.     public boolean isConnected(int p, int q) {
    28.         return find(p) == find(q);
    29.     }
    31.     /**
    32.      * 合并两个元素
    33.      * 时间复杂度为 O(n）
    34.      * @param p
    35.      * @param q
    36.      */
    37.     @Override
    38.     public void unionElements(int p, int q) {
    39.         int pID = find(p);
    40.         int qID = find(q);
    42.         if(pID == qID)
    43.             return;
    45.         for(int i = 0;i < id.length; i++) {
    46.             if(id[i] == pID)
    47.                 id[i] = qID;
    48.         }
    49.     }
    51.     /**
    52.      * 查找元素p所对应的集合编号
    53.      * 时间复杂度为 O(1)
    54.      * @param p
    55.      * @return
    56.      */
    57.     private int find(int p) {
    58.          return id[p];
    59.     }
    61. }
    • implementation2

    与上述实现不同，连接两个集合不再把某个集合的所有节点都连接到另一个集合的根节点，而是直接把两个集合的根节点直接相连。数组维护的是父节点不再是根节点，父节点不一定是根节点。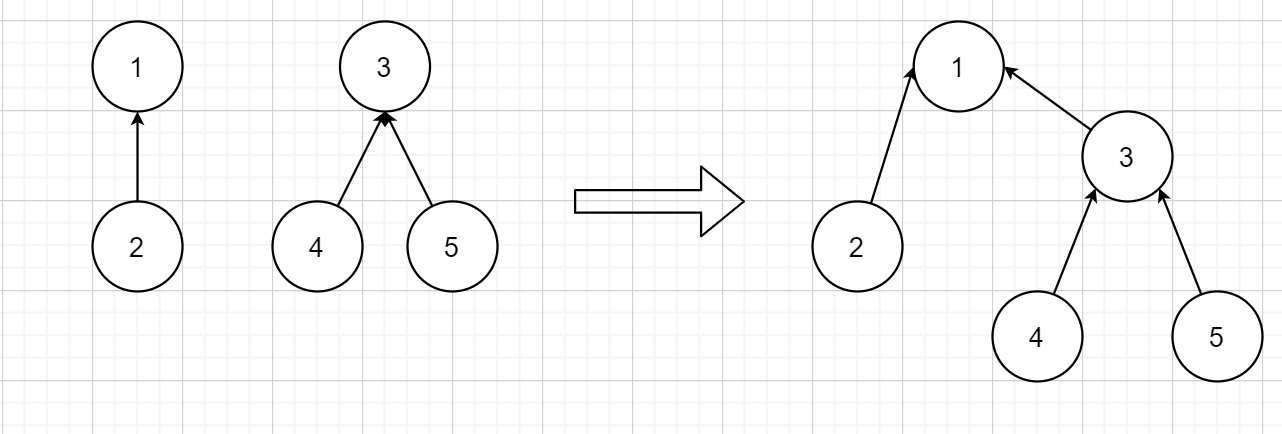
    image.png

    1. public class UnionFind_v2 implements UF {
    3.     private int[] parent;
    5.     public UnionFind_v2(int size) {
    7.         parent = new int[size];
    9.         for(int i = 0; i < size; i++) {
    10.             parent[i] = i;
    11.         }
    12.     }
    14.     @Override
    15.     public int getSize() {
    16.         return parent.length;
    17.     }
    19.     @Override
    20.     public boolean isConnected(int p, int q) {
    21.         return find(p) == find(q);
    22.     }
    24.     /**
    25.      * 合并元素
    26.      * 时间复杂度为O(H)
    27.      * @param p
    28.      * @param q
    29.      */
    30.     @Override
    31.     public void unionElements(int p, int q) {
    32.         int pRoot = find(p);
    33.         int qRoot = find(q);
    35.         if(pRoot == qRoot)
    36.             return;
    38.         parent[pRoot] = qRoot;
    39.     }
    41.     /**
    42.      * 查找p元素的根节点
    43.      * 时间复杂度是O(H)
    44.      * @param p
    45.      * @return
    46.      */
    47.     private int find(int p) {
    48.         while(p != parent[p])
    49.             p = parent[p];
    51.         return  p;
    52.     }
    54. }

    当然还有些优化，比如找到根节点时候进行路径压缩，或者直接用递归。

    1.     private int find(int p) {
    2.         while(p != parent[p]) {
    3.             parent[p] = parent[parent[p]];//路径压缩
    4.             p = parent[p];
    5.         }
    6.         return  p;
    7.     }

    如果需要所有节点都指向根节点，也可以在find方法里递归调用。

    1.     private int find(int p) {
    2.         if(p != parent[p]) {//递归保证所有节点都指向根节点
    3.             parent[p] = find(parent[p]);
    4.         }
    6.         return  parent[p];
    7.     }

    除此之外，我们还可以维护集合树的高度和节点树等。。。例题等下碰到比较经典的再write down。