• 判断奇偶数：x & 1 = 1则为奇数 / =0 则为偶数。因为奇数二进制的最后一位为1，偶数二进制最后一位为0
    • 判断二进制位是1还是0
    • 交换两个整数变量的值
    • 求整数的绝对值

    题1：
    找出 [1, 1000] 唯一成对的数：
    异或^, 但是我们不能直接将数字直接异或，因为不同的数异或为1，相同的数异或为0，那么重复的数异或等于0，得不到想要的结果，对于这种已知有范围的数字，我们先异或这个范围所有的数，这样不同的数相当于存在两个，而重复的数存在3个，这样异或得到的就是重复的数。（位运算满足交换律, 0 异或任何数等于本身。）
    找出唯一落单的数就可以直接异或。

    题二：
    二进制中一的个数：
    1. 不断右移 & 1 == 1 计数；
    2 x & (x - 1)把低位第一个为1的位置变成0，所以当x == 0时，计算总共操作了几次。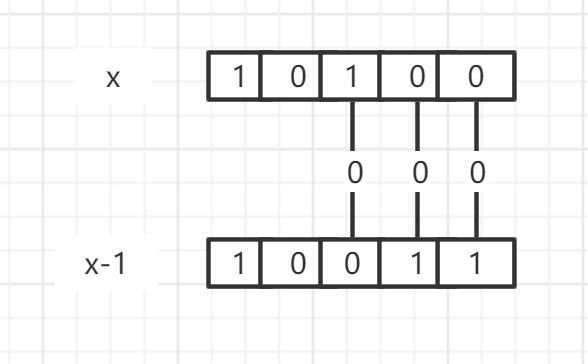
    image.png

    题四：
    一条语句判断一个整数是不是2的整数次方。
    解：相当于判断二计制位只有一位为1。 x & (x - 1) ? == 0

    题五：
    将整数二进制的奇偶位互换
    解：分别取奇数位和偶数位，然后偶数位左移，奇数位右移，两者再做异或运算。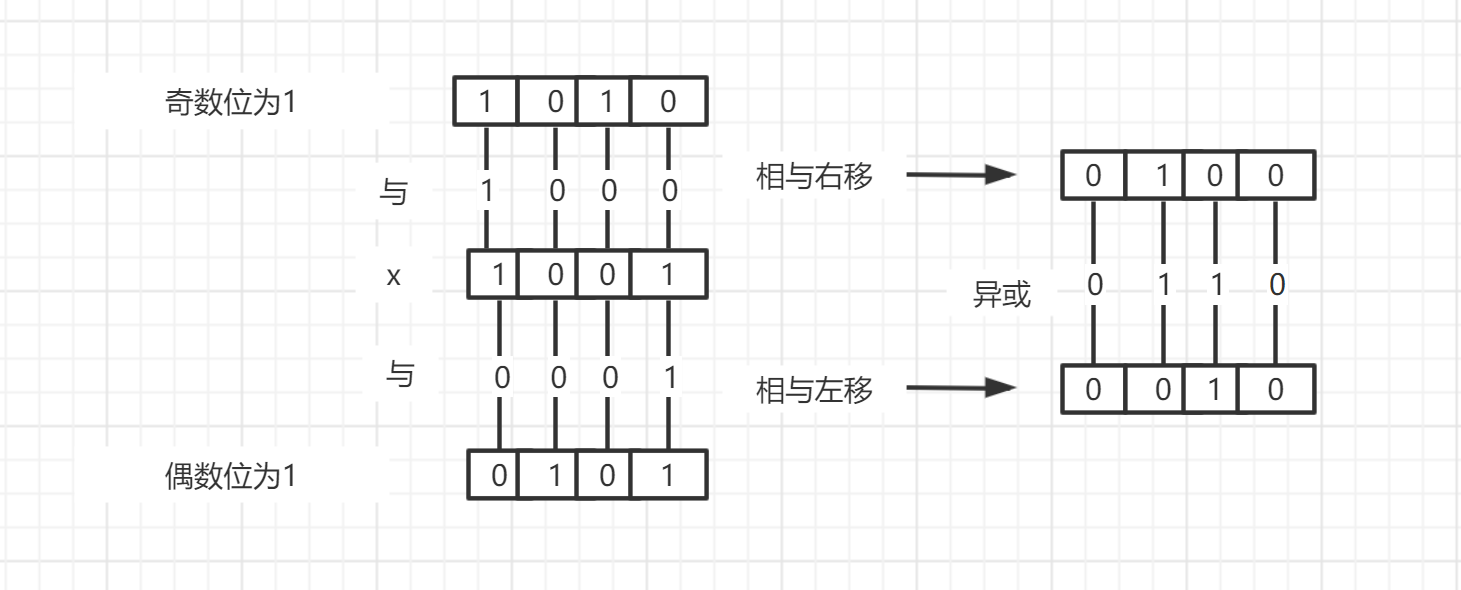
    image.png

    题六：
    给一个0-1之间的实数，如0.625，输出它的二进制表示。如0.625——>0.101
    解： 0.625 2 = 1.25 取整数部分1 并去除整数部分（-1）
    0.25     2== 0.5 取0
    0.5 * 2 == 1 取 整体部分1去除整数部分（-1）

    题7：
    出现K次和出现1次的数，找出出现一次的数。
    解：将所有数转化成K进制， 原因是，该题和题1的区别在于K=2，所以使用二进制的异或，因为异或相当于不进位的加法，它可以使出现了两次相同的数变成0，同理当K = 3时，我们希望出现三次的数变成0，我们使用三进制的异或。从数学角度来讲，当一个数出现K次，那么相加他一定是K的倍数，之前讲到异或相当于不进位的加法，其实也就是相加取余，再因为相加之和是K的倍数，取余等于0.