其实对回溯法一直不是很理解，主要还是对递归不够理解。先从最简单的回溯开始。

    回溯法 - 图1

    • 回溯法

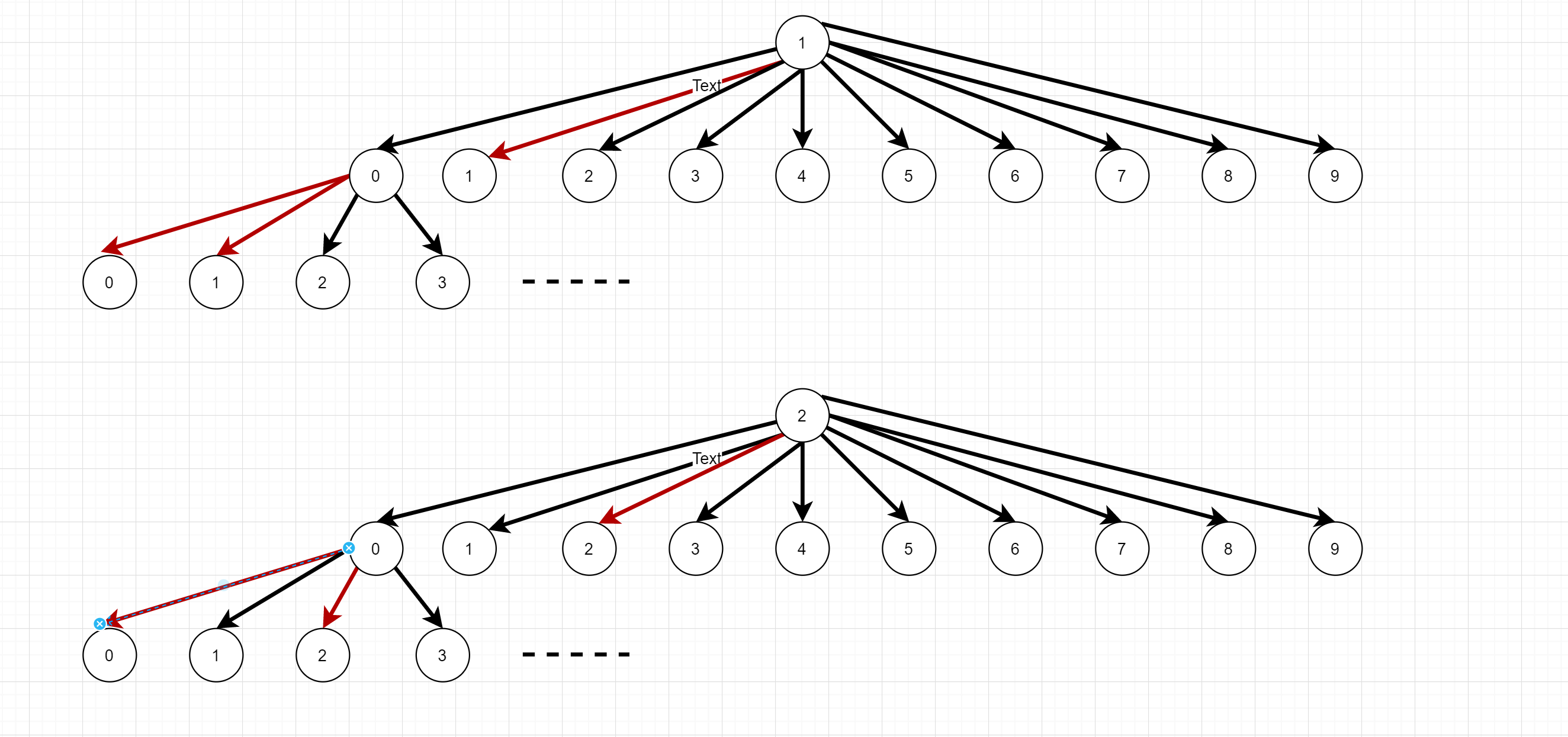
    image.png
    其实回溯和树的遍历dfs差不多，对于这道题当n = 3时， 我们先遍历1开头，10， 102，。。。，在120，。。。。，在遍历2开头，2，20，201，、、、、。
    需要注意的是，以0开头的不需要遍历，最后加上0就行。

    1. import java.util.HashSet;
    3. public class Main {
    4.     static int count = 0;
    5.     public static void main(String[] args) {
    6.         countNumbersWithUniqueDigits(2);
    7.     }
    8.     public static int countNumbersWithUniqueDigits(int n) {
    9.         HashSet<Integer> hashSet = new HashSet<>();
    10.         fun(0, n, hashSet);
    11.         System.out.println(count);
    12.         return count;
    13.     }
    14.     public static void fun(int num, int n, HashSet<Integer> hashSet) {
    15.         if(hashSet.size() == n) {
    16.             System.out.println(num);
    17.             return;
    18.         }
    19.         System.out.println(num);
    22.         for(int i = 0; i <= 9; i++) {
    23.             if(hashSet.contains(i) || (hashSet.size() == 0 && i == 0))
    24.                 continue;
    25. //            System.out.println(num);
    27.             count++;
    29.             hashSet.add(i);
    31.             fun(num * 10 + i,  n, hashSet);
    32.             hashSet.remove(i);
    34.         }
    35.     }
    36. }

    • 动态规划

      dp[ i ]代表前 i 位可能会出现重复数字的数目。分以下两种情况
      1.如果前 i - 1 有重复的情况，那么第 i 位 随便取(0 ~ 9)一个数都是重复数字， 所以dp[ i ] = 10 dp[ i - 1]
      2.如果前 i - 1 没有重复的情况，那么取 前 i - 1的数字中的任何一个都会造成重复 dp[ i ] = (9       10 - dp[i - 1]) (i - 1).
      9       10表示 i - 1位有这么多组合，为什么不是10??? 因为10还包括了小于i - 1位的情况，也就是第一个数字等于0.必须排除这种情况。
      然后减去重复的数目
      综上所述 dp[i] = 10 dp[ i - 1] + (9 10 - dp[i - 1]) * (i - 1)
      最后将10减去dp总和
      初始化
      d[0] = 0 , 对于0位数字不可能有重复的数字
      d[1] = 0 , 对于1位数字也没有重复

      1. class Solution {
      2. public:
      3.   int countNumbersWithUniqueDigits(int n) {
      4.       int* d = new int[n+1];
      5.       memset(d, 0, sizeof(int)*(n+1));
      6.       for (int i = 2; i < n+1; ++i)
      7.       {
      8.           d[i] = d[i-1]*10 + (9*pow(10, i-2)-d[i-1])*(i-1);
      9.       }
      11.       int sum = 0;
      12.       for (int i = 0; i < n+1; ++i)
      13.       {
      14.           sum += d[i];
      15.       }
      16.       return pow(10, n) - sum;
      17.   }
      18. };

    • 背包问题

    **

    • 八皇后