直方图的水量

oh，又一次败北，惜败惜败，毕竟是困难，可是也没那么难，还是思之毫厘，差之千里。这道题的关键思路在于，如何计算两柱之间包含其他柱的情况下的水量，我的思路是找到局部最大的左柱子 left 和右柱子 right，那么它们之间的水量就等于 Math.min ( height[ left ], height[ right ]) * (right - left - 1) 再减去他们之间的所有低柱子，这样会出现很多问题。首先这种计算方式就是有问题的。如果运行局部思想找到的就只有红色区域，但其实还包括上面的白色区域。但是这种局部思想是可以的，我们不用减而是用加，比如下图我们先算红色区域，在加上白色区域即可。首先我们碰到比栈顶元素要大的柱子是可以存水的，然后栈顶元素（top）出栈，水量的高度等于左右两边柱子的最低高度， 此时左边柱子是等于此时栈的栈顶元素（left），右边柱子是 i， height = min(height[ left ], height[ i ]) - height[top]。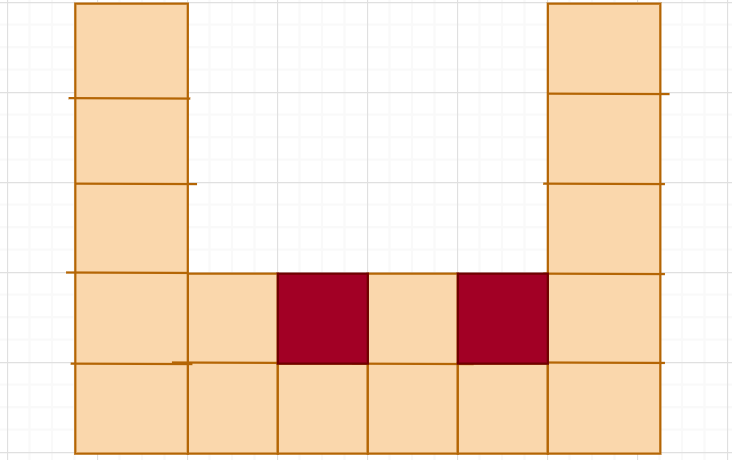

class Solution {
    public int trap(int[] height) {
        int ans = 0;
        Deque<Integer> stack = new LinkedList<Integer>();
        int n = height.length;
        for (int i = 0; i < n; ++i) {
            while (!stack.isEmpty() && height[i] > height[stack.peek()]) {
                int top = stack.pop();
                if (stack.isEmpty()) {
                    break;
                }
                int left = stack.peek();
                int currWidth = i - left - 1;
                int currHeight = Math.min(height[left], height[i]) - height[top];
                ans += currWidth * currHeight;
            }
            stack.push(i);
        }
        return ans;
    }
}