dfs 深度优先遍历可以递归和非递归；

    1. queue=collections.deque([])
    2. queue.append(第一个满足条件的点)
    3. while queue 不空：    
    4.     cur = queue.popleft()    
    5.     标记我们访问过cur这个点，从而之后不会再访问到这个点    
    6.     for 节点 in cur的所有相邻节点：        
    7.         if 该节点有效且满足条件：            
    8.             queue.append(该节点)            
    9.             标记我们访问过这个节点

    标记我们访问过这个节点应在入队列时而不是出队列时。

    bfs 广度优先搜索用队列非递归，但是可以递归吗？？？

    • 染色法

    适用于二分图（leecode886. 可能的二分法）
    1.先构造图（邻接表ArrayList<Integer>[] graph或邻接矩阵）
    2.遍历访问未访问的节点然后dfs
    3.dfs：若此时节点已访问过，若标记颜色不等于节点原本的颜色，则返回false；若此时节点未访问过，给该节点上标记颜色，并且用相反的颜色标记该节点的邻居节点。（标记访问和标记颜色可以用一个数组，0表示未访问，1和-1表示已访问并上不同的颜色）

    • 图有环

    在考虑（leecode886. 可能的二分法）这道题的时候，首先的思路是判断是否有环，然后发现即使有环也可能是二分图，比如下左图([1,3],[2,4])，但是我发现，当这个环的个数为奇数时，必有一个节点无法满足条件（还没验证该想法的准确性）, 开始判断环的思路是如果在dfs过程中访问到了已访问过的节点且不是上一次访问的节点（怎么记录环的个数可以深思），网上都说需要加一个状态表示某节点的所有邻接节点都访问完（我们标记为2），单纯一个数组表示节点已访问（我们标记为1）是不够的。算法则为：如果遍历的过程中发现某个节点有一条边指向标记为1的节点（也就是说不能为2），那么存在环。为什么要加上这个为2的状态，按道理如某个节点的所有邻接点都被访问过的话，就不会还存在一个节点指向它？？？
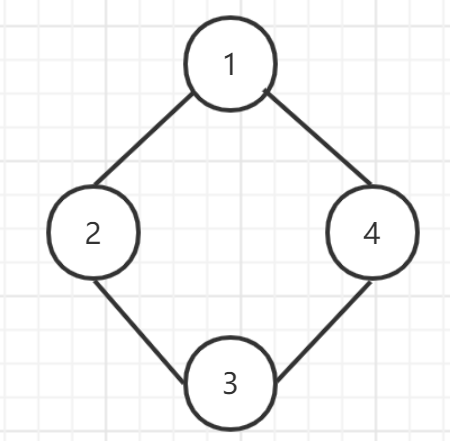
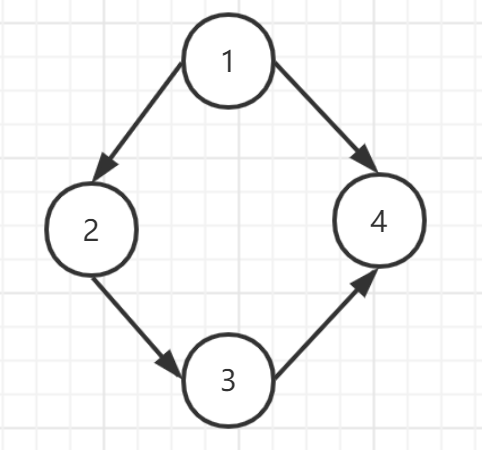
    image.pngimage.png

    研究了半天，想法没有错，只是忽略了一个问题，有向无环图和无向无环图判断是否有环是不一样的，上面两张图，左边是无向图有环，右边是有向无环图（看起来好像是一个环，但是不满足环的定义X-Y, Y-Z, Z-X. 得回到起点）。所以说网上讲的状态三是在有向图的基础上，无向图判断只需是否节点访问过并且不是父节点即可。

    我们进一步扩展，如何记录环的个数或者说记录环的节点编号？只需在dfs加上一个数组记录每次递归的父节点的编号，当碰到有环的时候反向输出即可。

    1. //有向图
    2. void dfs(int root) {
    3.     color[root] = 1;
    4.     for(auto child : g[root]) {
    5.         if(color[child] == 1) {
    6.              hasCycle = true;
    7.              break;
    8.         }
    9.         else if(color[child] == 0) {
    10.             dfs(child);
    11.         }
    12.     }
    13.     color[root] = 2;
    14. }
    16. //无向图
    17. void dfs(int root, int parent) {
    18.     color[root] = 1;
    19.     for(auto child : g[root]) {
    20.         if(color[child] == 1 && child != parent) {
    21.              hasCycle = true;
    22.              break;
    23.         }
    24.         else if(color[child] == 0) {
    25.             dfs(child, root);
    26.         }
    27.     }
    28. }