本来想看看关于并查集的例题，结果和最下生成树有关，所以温习下。其实第一次接触最小生成树是在大二的时候，至今为止差不多三年了，中间也刷过题，到现在只记得大概。算法一天不练就生疏，今天立个flag，每天至少刷一道算法题并且掌握其原理然后举一反三。嗯嗯，就这么办。

    大家都知道有Prime和kruskal算法，
    先介绍Prime算法。一个话概括就是找到局部最短路径从而找到全局最短路径，为什么局部最优能够找到全局最优？？？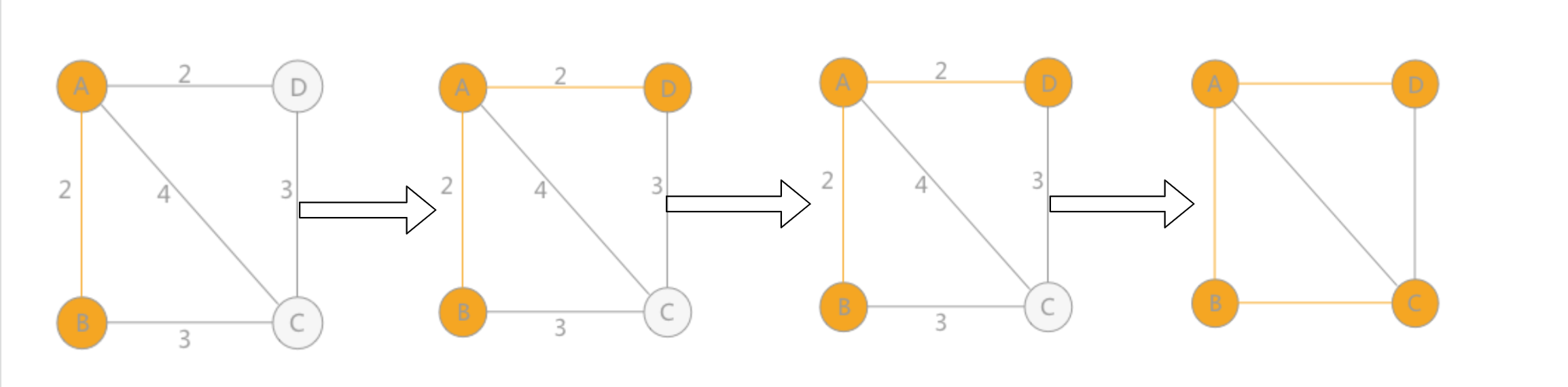
    image.png

    1. import java.util.HashMap;
    2. import java.util.HashSet;
    4. //代码没有运行，全靠逻辑思维。哈哈哈
    5. public class Main {
    6.     public static void main(String[] args) {
    7.         int[][] graph = new int[][]{};
    8.         prime(graph, 0);
    9.     }
    10.     public static void prime(int[][] graph, int start) {
    11.         HashSet<Integer> path = new HashSet<>(); //用来保存生成树的节点
    12.         path.add(start);
    14.         while(path.size() < graph.length) {
    15.             int min = Integer.MAX_VALUE;
    16.             int to = 0;
    18.             for (int node : path) {
    19.                 for (int j = 0; j < graph.length; j++) {
    20.                     //首先没有访问过，并且有连边的前提下找到但当前最短连边。
    21.                     if (!path.contains(j) && graph[node][j] != 0 && graph[node][j] < min) {
    22.                         min = graph[node][j];
    23.                         to = j;
    24.                     }
    25.                 }
    26.                 path.add(to);
    27.             }
    28.         }
    29.     }
    30. }

    Kruskal我是没有任何印象的，只能说每次掌握的都没有很牢靠，没有真正理解。
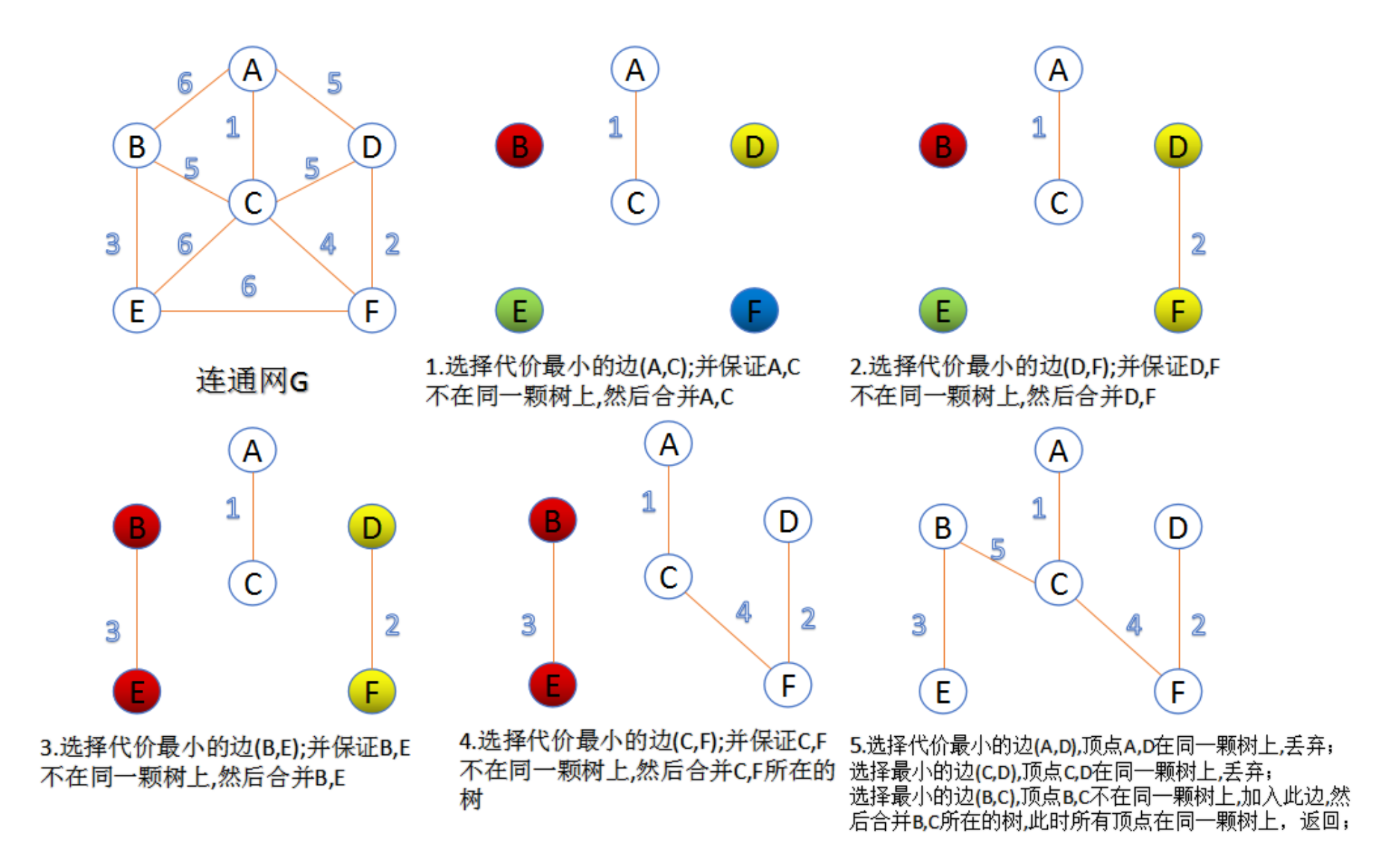
    此算法可以称为“加边法”，初始最小生成树边数为0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。
    1. 把图中的所有边按代价从小到大排序；
    2. 把图中的n个顶点看成独立的n棵树组成的森林；
    3. 按权值从小到大选择边，所选的边连接的两个顶点ui,viui,vi,应属于两颗不同的树，则成为最小生成树的一条边，并将这两颗树合并作为一颗树。
    4. 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。

    这炸眼一看不就是并查集的思路吗？？难怪并查集和最小生成树放在一起。排序的话，因为它每次都去最小的边，所有我们可以用堆排序。
    image.png