感觉对字符串的问题没有一个系统的总结，所以打算记录下比较经典的题目。

    3. 无重复字符的最长子串 字符串 - 图11.第一种方法我是用双重循环，加入以i为起点，用 j 遍历到出现了i，j之间相同的字符用让起点 i++。

    1. public class Solution_1 {
    2.     public static void main(String[] args) {
    3.         System.out.println(lengthOfLongestSubstring("bbbbb"));
    4.     }
    5.     public static int lengthOfLongestSubstring(String s) {
    6.         char[] ch = s.toCharArray();
    7.         int max = 0;
    8.         for(int i = 0; i < ch.length; i++) {
    9.             String str = "";
    10.             for(int j = i; j < ch.length; j++) {
    11.                 if(str.indexOf(ch[j]) == -1)
    12.                     str = str + ch[j]+"";
    13.                 else
    14.                     break;
    16.             }
    17.             max = max > str.length() ? max : str.length();
    18.         }
    19.         return max;
    20.     }
    21. }
    1. 用集合 set代替一重循环，因为set有cantains。 ```java import java.util.HashMap; import java.util.HashSet;

    public class Solution_2 { public static void main(String[] args) { System.out.println(lengthOfLongestSubstring(“bbbbb”)); } public static int lengthOfLongestSubstring(String s) { int max = 0; HashSet set = new HashSet<>();

    1.     int i = 0, j = 0;
    2.     //滑动窗口
    3.     while(i < s.length() && j < s.length()) {
    4.         if(!set.contains(s.charAt(j))) {
    5.             set.add(s.charAt(j++));
    6.             max = Math.max(max, j - i);
    7.         }
    8.         else
    9.             set.remove(s.charAt(i++));
    10.     }
    11.     return max;
    12. }

    }

    2. 3. 可以在起点上做一点优化，起点不需要依次递增，如果出现重复字符，只需把起点移动到 string（i，j）之间的那个重复字符的下一位即可。如图所示，当子串abcd 又碰到c时， 按以前方法，起点 i 还要依次从b和c开始，但是不需要这么做，因为只要c还在，那么字串 b c d c， c d c 一定会出现相同字符，而且长度一定小于 a b c d c，所以起点完全可以从 d 开始。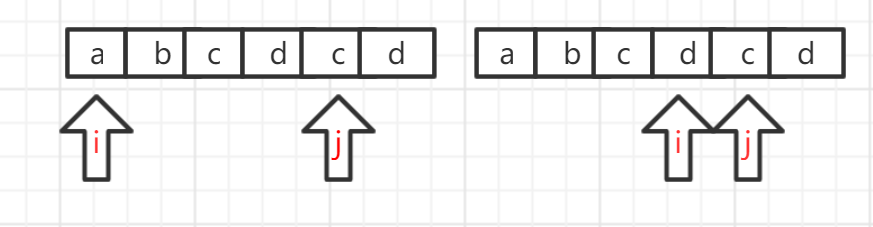
    4. ![image.png](https://cdn.nlark.com/yuque/0/2021/png/438944/1618038201838-ec9c3d94-e3bf-4c1b-b8e5-87749c17ab66.png#align=left&display=inline&height=170&margin=%5Bobject%20Object%5D&name=image.png&originHeight=227&originWidth=873&size=26160&status=done&style=stroke&width=655)
    5. ```java
    6. import java.util.HashMap;
    7. import java.util.Map;
    9. public class Solution_3 {
    10.     public int lengthOfLongestSubstring(String s) {
    11.         int n = s.length(), ans = 0;
    12.         Map<Character, Integer> map = new HashMap<>(); // current index of character
    13.         //关键在于i的优化，在当前子串索引i到j。如果包括末端j字符，那么i直接跳到子串中相同元素位置m，因为只要有m存在，那么字串就无法向后移动
    14.         // try to extend the range [i, j]
    15.         for (int j = 0, i = 0; j < n; j++) {
    16.             if (map.containsKey(s.charAt(j))) {
    17.                 i = Math.max(map.get(s.charAt(j)), i);
    18.             }
    19.             ans = Math.max(ans, j - i + 1);
    20.             map.put(s.charAt(j), j + 1);
    21.         }
    22.         return ans;
    23.     }
    24. }

    5. 最长回文子串 字符串 - 图21.我开始的思路是遍历每个字符，然后循环判断该两边的字符是否相同。这样问题就是只适合回文串是奇数的时候。所以当回文串是偶数我们需要从 i 和 i + 1两个相邻的位置同时往外延伸。然后取两者最大值。

    1. public class Solution_3 {
    2.     public static void main(String[] args) {
    3.         System.out.println(longestPalindrome("abba"));
    4.     }
    5.     public static String longestPalindrome(String s) {
    6.         if(s.equals(""))
    7.             return "";
    9.         int maxLength = 0, start = 0, end = 0;
    11.         for(int i = 0; i < s.length(); i++) {
    12.             int len1 = fun1(s, i, i); //以当前i位置字符为中心向两边延伸
    13.             int len2 = fun1(s, i, i + 1); //以i位置和i+1位置的中心向两边延伸
    15.             maxLength = Math.max(len1, len2);
    17.             if(maxLength > end - start) {
    18.                 start = i - (maxLength - 1) / 2; //当回文串为奇数，中心节点就是i， 可以直接减去 maxLength / 2 ，
    19.                                             // 但是回文串为偶数时， 中心节点时 i和i+1之间的点，此时索引=i和中心节点与左半回文串相差 1/2
    20.                                             // 减去(maxLength - 1) / 2
    21.                                             //当回文串为奇数 maxLength / 2 == (maxLength - 1) / 2，所以无需分类讨论
    23.                 end = maxLength / 2 + i; //奇数同理直接加上maxLength / 2 同理回文串为偶数时，中心节点时 i和i+1之间的点，此时索引=i和中心节点与右半回文串相差 1/2
    24.                                             //但是maxLength / 2 == (maxLength + 1) / 2
    25.             }
    26.         }
    27.         return s.substring(start, end + 1);
    28. }
    30.     private static int fun1(String s, int left, int right) {
    32.         while(left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
    33.             left--; right++;
    34.         }
    35.         return right - left - 1;
    36.     }
    37. }

    14. 最长公共前缀 字符串 - 图3暴力解法肯定可以的，这里主要采用了字典树，包括初始化树的结构， 这里不再是左右子树，而是26个，所以我们需要一个集合，而且还需要根据恰当的索引找到对应的字典树节点， 所以采用了HashMap。 方法主要包括增加字符串， 获取最长公共前缀等等。

    1. import java.util.TreeMap;
    5. public class Solution_2 {
    6.     public static void main(String[]args){
    7.         System.out.println(longestCommonPrefix(new String[]{"flower","flow","flight"}));
    8.     }
    9.     public static String longestCommonPrefix(String[] strs) {
    10.         Trie trie = new Trie();
    11.         for(int i = 0; i < strs.length; i++) {
    12.             trie.add(strs[i]);
    13.         }
    14.         return trie.searchLongestPrefix();
    16.     }
    22. }
    23. class Trie {
    24.     private class TrieNode {
    25.         public int size; //当前节点有多少个子节点
    26.         public TreeMap<Character, TrieNode> nodes; //当前节点的链接节点
    27.         public boolean isEnd; //是否是一个单词
    29.         public TrieNode(boolean isEnd) {
    30.             this.isEnd = isEnd;
    31.             nodes = new TreeMap<>();
    33.         }
    34.         public TrieNode() {
    35.             this(false);
    36.         }
    38.     }
    40.     TrieNode root;
    42.     public Trie() {
    43.         root = new TrieNode();
    44.     }
    46.     public void add(String string) {
    47.         TrieNode cur = root;
    48.         for(int i = 0; i < string.length(); i++) {
    49.             char c = string.charAt(i);
    50.             if(cur.nodes.get(c) == null)
    51.                 cur.nodes.put(c, new TrieNode());
    53.             cur = cur.nodes.get(c);
    54.         }
    55.         cur.isEnd = true;
    56.     }
    58.     //找出字典树中的最长前缀
    59.     public String searchLongestPrefix() {
    60.         String prefix = "";
    61.         TrieNode node = root;
    63.         while(!node.isEnd && node.nodes.size() == 1) {
    64.             char c = node.nodes.firstKey();
    65.             prefix += c+"";
    66.             node = node.nodes.get(c);
    67.         }
    68.         return prefix;
    69.     }
    70. }

    最长公共子串
    题目描述：给定两个字符串，求出他们之间最长相同子字符串长度。
    1、 状态定义：dp[i][j]表示以s1[i]和s2[j]为最后一个元素的最长公共子串，如果最长公共子串存在，公共子串的最后一个元素一定是s1[i]或者s2[j]他们相等。
    2、 状态转移方程：
    如果s1[i]和s2[j]相等，那么：dp[i][j] = dp[i-1][j-1]+1；
    如果s1[i]和s2[j]不相等，则：dp[i][j] = 0；
    3、 初始化：初始dp[0][j]和dp[i][0]都为false
    4、 输出：dp[i][j]的最大值

    1.     public int longestCommonString(String s1,String s2) {
    2.         int[][] dp = new int[s1.length()+1][s2.length()+1];
    3.         int maxlen = 0;
    4.         for (int i = 1; i <= s1.length(); i++) {
    5.             for (int j = 1; j <= s2.length(); j++) {
    6.                 if(s1.charAt(i-1)==s2.charAt(j-1))
    7.                     dp[i][j] = dp[i-1][j-1]+1;
    8.                 else
    9.                     dp[i][j] = 0;
    10.                 maxlen = Math.max(maxlen, dp[i][j]);
    11.             }
    12.         }
    13.         return maxlen;
    14.     }