写在前面
上学的时候，有一门综合评价的课程，那时候没觉得以后会用到它，现在才发现是那么实用，实际应用中如果采用单指标进行评价给人的感觉总是有偏驳的，除非是那种极其可靠且明确其重要性的指标。近期基本上把老课本里的方法翻了个老底，以前觉得这门课程似乎挺难的，现在看来只是以前没有深入的好好看，方法简单且实用。
综合评价的方法一般是主客观结合的，方法的选择需基于实际指标数据情况选定，最为关键的是指标的选取，以及指标权重的设置，这些需要基于广泛的调研和扎实的业务知识，不能说单纯的从数学上解决的。
以下几种方法都是在实际中应用过的，在实际应用的我们遇到的状况，也描述一下。
指标的正向化
指标一般分为正向指标（越大越好）、逆向指标（越小越好）、适度指标（不能太小也不能太大）。为了可以进行综合汇总，需要解决同方向性，一般需要将逆向指标和适度指标正向化。
逆向指标正向化
- 倒数法：
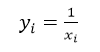
- 最小阈值法：
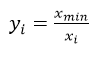
- 最大阈值法（互补法）：
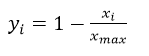
适度指标的正向化
- 绝对值倒数法：反应了实际值与标准值之间的偏差，偏差越小越好，对应的转化后的值越大，达到正向化的目的；
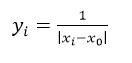
- 距离倒数法：跟绝对值倒数法类似
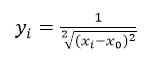
指标的无量纲化
指标的无量纲化可以消除指标间量级不同的影响，可以使各个指标转化成可以直接加减的的数值，常用的消除定量指标无量纲化的方式如下
1、阈值比较法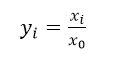
x0表示阈值，阈值设置的越大，评价指标的反应越迟钝，过小会过于灵敏，需根据实际需求确定，动态评价可以是被评价对象的历史最优水平，也可以是基期水平，若为计划完成情况，可以为计划数，对实际水平的评价可以是同类被评价对象的最好水平或平均水平，阈值大小是可以不断调整的。
2、中心化也称均值化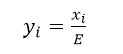
此处的E可以是算术平均值，也可以是中位数、总数，根据实际需求来定。
3、规格化，最常用的就是这种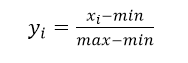
无量纲化之后，数据范围0-1之间，表明了数据在全距中的相对位置。
4、标准化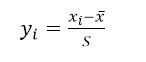
该方法适用于数据量较大的情况，样本数要在30以上，评价值在-1至1之间。
5、比重法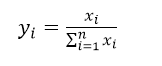
或
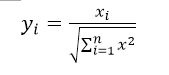
应用数据的结构指标来消除量纲的影响，前一种不适用于有负值的情况，后一种可以根据具体情形用于含负值的情况。
以上均为直线型处理方法，也较为常用，其他分段处理的情况可以再扩展。指标权重设置
主观赋权法
1、主观赋权法，又称专家赋权法，这个方法还是不要轻易用吧，除非你就是权威或者咨询了权威。
2、层次分析法（AHP），综合多个人的进行指标间重要性评价，将主客观结合在一起得出权重，之前有写过一个文档，见末尾模糊综合评价部分权重获取附带的链接。
以上两种均为主观赋权法，也有比较偷懒不能明确指标间的重要性，采用等权法。
客观赋权法
基本思想是利用各指标间的相互关系或提供的信息量来确定，实际通过对原始数据经过数学处理获取权重，原始数据所包含的信息包括两种，一种是指标变异程度上的信息差异，一般通过指标的标准差或变异系数来反映，一种是指标间的相互影响程度，这种信息一般隐含在指标见相关关系矩阵中，以下几种赋权方法均是基于该两点进行的；
1、变异系数法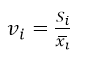
，然后再进行归一化化处理，得到各个指标的权重。
其中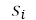
表示标准差，公式就不写了，i表示指标，分母表示均值，标准差的计算中，30个以上的数据使用n，30个样本以内使用n-1，我们都知道标准差反应了数据的平稳性，由变异系数来反映数据所含信息量的大小；
2、相关系数法
相关系数法是根据指标间的相关程度来确定各个指标重要性程度的方法，一般来说某一个评价指标与指标体系中的其他指标信息重复越多，说明该指标的变动越能被其他指标的变动所解释，则该指标的变动越能够被其他指标的变动所解释，所以赋给其的权重越小。这个让我想起了多重共线性，也是一种筛选指标的方法之一。
2.1 由于研究的是多指标综合评价，首先需构建相关系数矩阵R；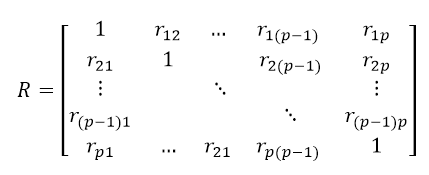
2.2 类似求矩阵的解，构造分块矩阵，求每个指标与其他指标的多元相关系数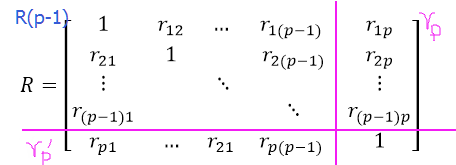
获取每个指标的多元相关系数
2.3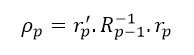
，具体怎么算参考线性代数，利用计算软件如R语言，可直接求逆矩阵；
2.4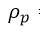
的值越大，说有与其他指标的相关性越大，其在综合评价中的作用越小，故确定权重时需进行正向处理，然后归一化。
2.5 各指标权重如下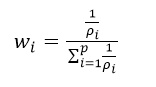
3、熵值法
熵值法本质上和变异系数法相类似，通过指标的离散程度来划分权重，熵值越大所包含的信息量就越大，对综合评价的影响越大，熵值得概念最初来至于物理学方面，可以自行百度，发现不同方面的理论知识是可以相互融合的，物理学和数学以及社会学似乎都有些东西是可以互相借鉴的。
3.1 指标的同向化，然后采用比重法将各个指标实际值转化为评价值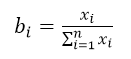
，
3.2 再计算每个指标的熵值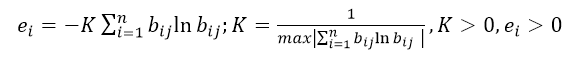
3.3 再计算差异系数dj=1-ej;
3.4 最后对差异系数进行归一化处理，获得各指标权重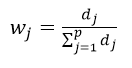
4、坎蒂雷赋权法
坎蒂雷赋权法假设指标与的指标间的线性加权的综合指数之间的相关系数是成比例的，将与综合指数高度相关的指标赋予较高的权重，反之赋予较小的权重。基于该假设，指标的权重为矩阵RS的最大特征根所对应的特征向量W，对W进行归一化处理，作为各个指标的权重，R为p个指标的相关系数矩阵，S为指标标准差所组成的对角矩阵。（PS这个方法没有尝试过）
主客观赋权方法的选择各有优劣，采用客观赋权法的结论有时候会与经验相悖，最好还是主客观结合比较合理。综合评价数值的综合方法
前面讲了指标权重的获取及无量纲化处理，将多指标进行综合的方法主要有四大类，线性综合法、几何综合法、混合综合法和模型综合法，简单来说就是加权求和、加权几何平均、线性加权与几何综合结合、模型综合法较为复杂，各个指标与综合指数间的关系，除却上述三种较为简单的以外，还有各种复杂的函数和相关关系，通过某种关系得到综合评价数值，该关系必须为描述对象间的关系清晰，可以用合适的数学表达式表述。以下列举的几种综合评价的方法均属于该范畴。综合评价方法
- 综合评分法
综合评分法是将各个指标转化为具体的分值后进行直接汇总的方式，主要是区间打分法和区间增量法；
区间打分法
区间打分法是划分等级，一般为5级，每个级别以2分递增，将指标按照划分标准进行打分，再基于确定好的指标权重，进行线性加权求和，得到综合得分。这种对于非连续型变量可适用，不受指标形式的限制，例如评价一个人的长相，评价一个人的长相处于ABCDE那个水平，每个级别对应的分数为10-8、8-6、6-4、4-2、2-0；
区间增量法
对各项指标的实际值，以同类指标的标准水平x0为基础进行打分,可取均值也可为其他值，每高出或低于标准水平，则分数对应提高或减少，程度由分母D决定，具体公式如下：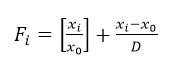
最后基于每个指标的得分，进行线性加权得到综合得分。
缺点，存在评价对象区分不明显的现象。 - 综合指数法
实际值与标准值进行对比后再使用线性综合汇总得到综合评分。
其中x0为标准值，需根据实际需求灵活设置，p表示评价指标个数，w表示权重，若把最小值设为0，则该公式等同于规格化后然后进行线性加权。
缺点是存在线性替代的现象。 - 秩和比评价方法
对各个指标或处理后的指标进行排秩，然后对秩进行加权综合处理，进行综合评价，但对于大数据量来说，成本较高。
秩和比计算公式如下，就是上面那句话的公式版乘100：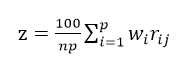
需注意的是秩和比是越小越好。 - 功效系数法
从公式中可以看出，实质上就是规格化后，增加两个调整参数，参数可以灵活设置，可以用来限定功效系数的取值范围。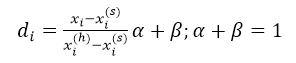
然后计算功效系数的综合值，可以采用线性综合法，也可采用几何综合法。
有一点不同于其他方法的权重设置，一般指标权重可以设置为任意实数，而功效系数法指标权重制定时，一般取1、2、3，1表示与其他评价指标相关的指标、2表示一般重要、3表示比较重要的指标，这个是在实践中总结的经验。 - 灰色关联度评价法
适用于指标数较少，需要选定最优序列，实际运用中效果不错。
基本原理如下，以前简单写下的：
需注意的是，最优序列的选择的根据实际需求来定，可以是某一行业标准值也可以是最大值什么的，记得逆向指标正向化，正向化的方法有很多种，这里没做说明，关联系数的公式构成其实跟规格化很像，只是采用的指数不同，分辨系数一般取0.5，可根据实际结果多次进行调整。另外计算出来的关联系数可能差距较小，这个可以根据个人需求做适当调整，调大两两之间的差距，且保持位势不变。 - 模糊综合评价
不建议使用这种方法，不适用于实际操作，指标重要性找几个人帮你挨个评价，然后计算合理性，总觉得不可实行，去年刚刚毕业工作时写的，现在看着写的挺傻的，怎么能想到这么用，但是是模糊综合评价的一个应用。
模糊综合评价应用。 - 因子分析
这种方式的在实际应用中可解释度相对较差，不直观。 - 其他降维方法
毕业论文写得是phd降维，还有sir…
若有收获，就点个赞吧
0 人点赞
