评价类模型——层次分析法，一致性检验

层次分析法（The Analytic Hierarchy Process即 AHP)是由美国运筹学家、 匹兹堡大学教授T . L. Saaty于20世纪70年代创立的一种系统分析与决策的综合 评价方法，是在充分研究了人类思维过程的基础上提出来的，它较合理地解决了定性问题定量化的处理过程。

AHP的主要特点是通过建立递阶层次结构，把人类的判断转化到若干因素两两之间重要度的比较上，从而把难于量化的定性判断转化为可操作的重要度的比较上面。在许多情况下，决策者可以直接使用AHP进行决策，极大地提高了决策的有效性、可靠性和可行性，但其本质是一种思维方式，它把复杂问题分解成多个组成因素，又将这些因素按支配关系分别形成递阶层次结构，通过两两比较的方法确定决策方案相对重要度的总排序。整个过程体 现了人类决策思维的基本特征，即分解、判断、综合，克服了其他方法回避决策者主观判断的缺点。

层次分析法：建模比赛中最基础的模型之一，其主要用于解决评价类问题（例如：选择哪种方案最好、哪位运动员或者员工表现的更优秀）。

评价类问题可用打分方法解决：

例题1：华中科技大学和武汉大学哪所学校好，考虑学习氛围、就业前景、男女比例、校园景色等因素。每个因素所占比例以及待比较的内容所占比例分配假设如下，则两所学校的评分计算方式为：

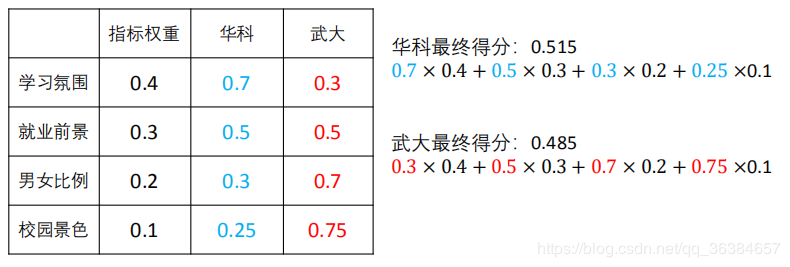
使用打分法解决评价问题，只需要我们补充完成下面这张表格即可：

例题2：小明同学想出去旅游，他选择苏杭、北戴河和桂林三地之一作为目标景点。请确定评价指标、形成评价体系为其选择最合适的方案。

第一步：

第二步：构建权重表格

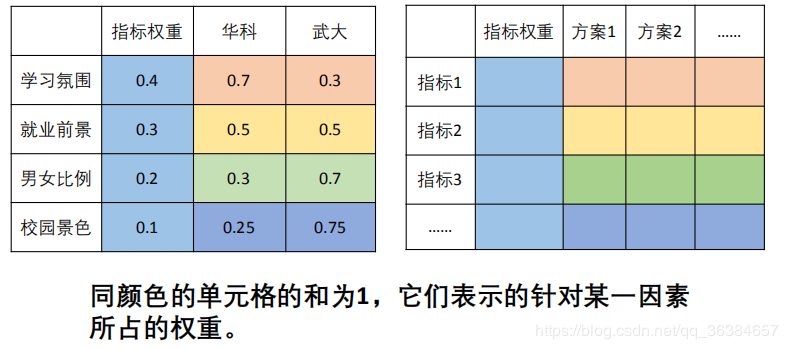
根据第一步的分析内容构建如下的权重表格，其中同色的之和为1：

如何填写上面的某种颜色的各项内容呢？例如蓝色对应的指标权重？

问题：
一次性考虑这五个指标之间的关系，往往考虑不周。

解决方法：
两个两个指标进行比较，最终根据两两比较的结果来推算出权重。

已知重要度表如下：

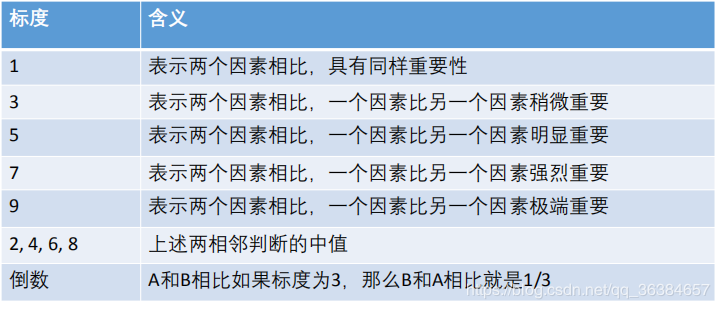
1、假设构建的指标权重的重要度比较矩阵如下：

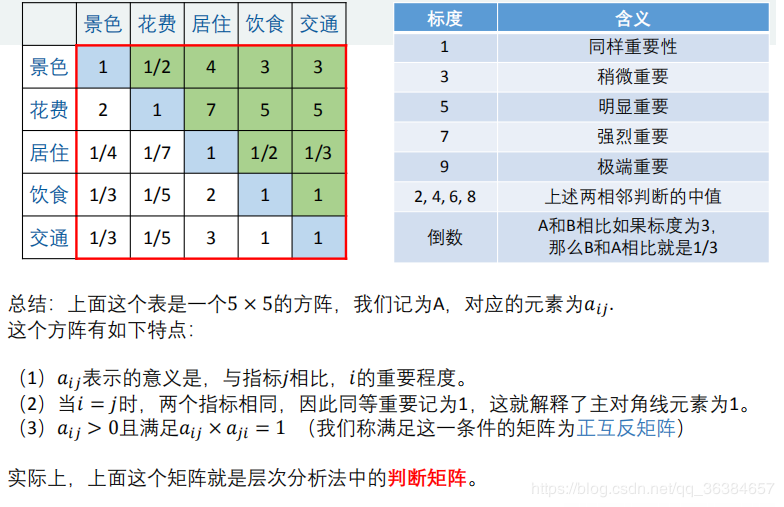
假设苏杭、北戴河、桂林在景色、花费、居住、饮食、交通方面的判断矩阵分别为：

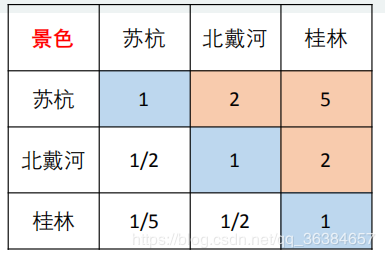
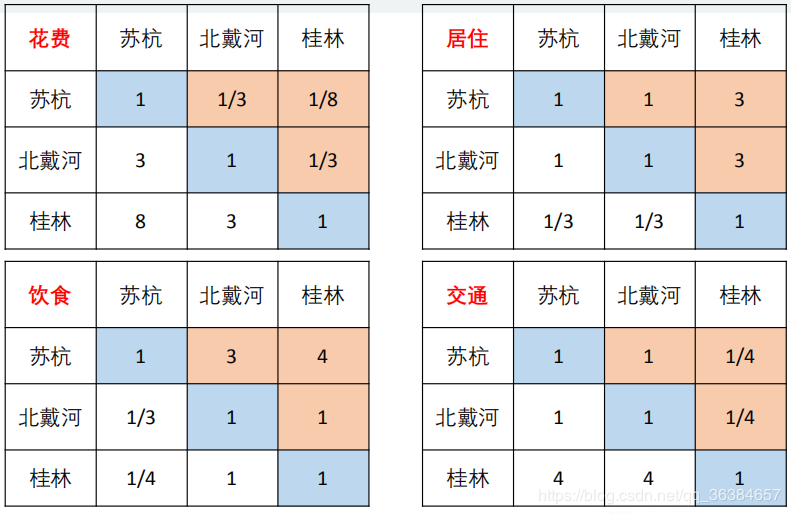
2、计算判断矩阵权重

总共三种方法计算权重：算数平均法、几何平均法、特征值法

1）、用算数平均法解决指标景色上的判断矩阵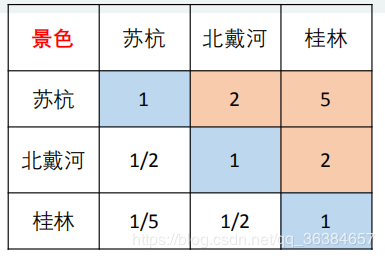

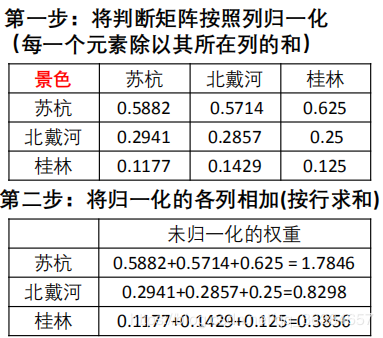
第一步：将判断矩阵按照列归一化 **（每一个元素除以其所在列的和）
第二步：将归一化的各列相加(按行求和**)
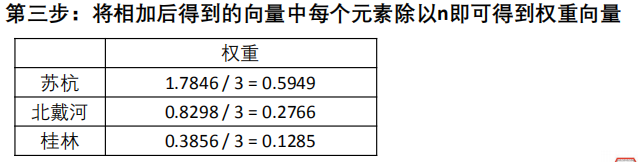
第三步：将相加后得到的向量中每个元素除以**n**即可得到权重向量
公式描述如下：

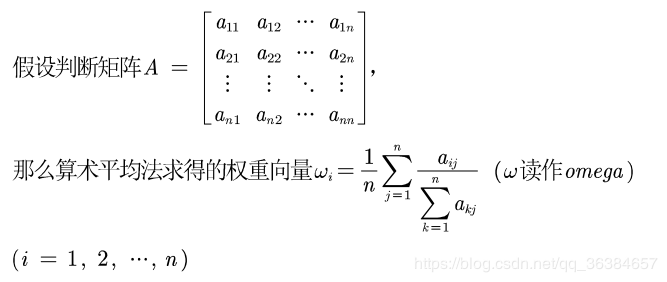
求解过程如下：

2）、用几何平均法解决指标景色上的判断矩阵

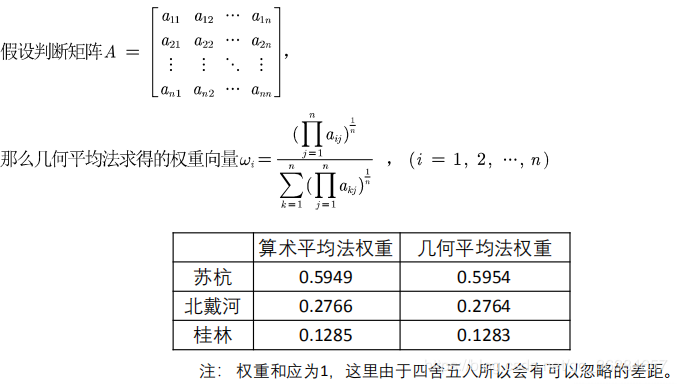
几何平均法求权重也有三步：
第一步：将A的元素按照行相乘得到一个新的列向量
第二步：将新的向量的每个分量开n次方
第三步：对该列向量进行归一化即可得到权重向量

**

3）、**用特征值法解决指标景色上的判断矩阵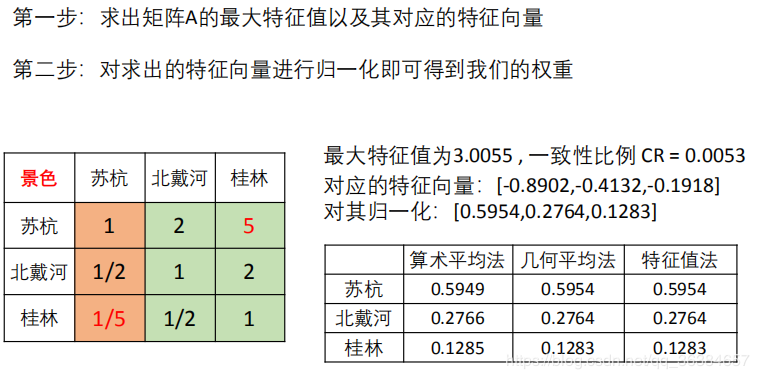

三种方法计算出来的结果差别较小，在此选用特征值法得到的结果填入对应的判断矩阵中：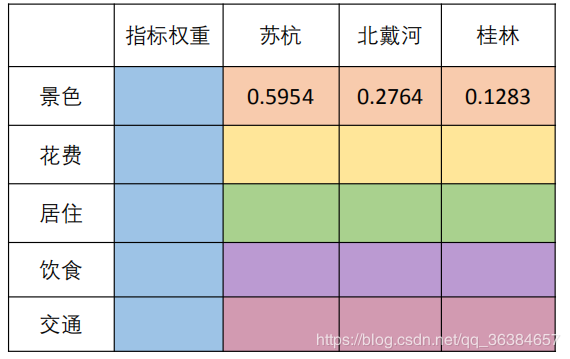

按照上述方法同理计算出其他色块对应的权重，得到使用特征值法求得的权重矩阵如下，根据此矩阵， 计算出每个旅游景点的得分。

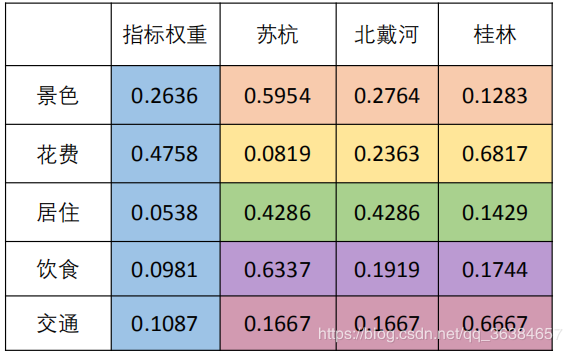
第三步：计算每个方案得分

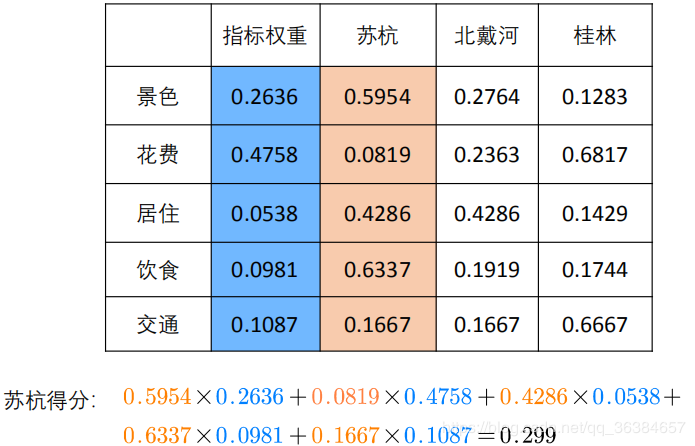
类似的，我们可以得到北戴河得分为0.245， 桂林得分为0.455. 因此最佳的旅游景点是桂林。

注意的问题：在第二步构造判断矩阵后要对其进行一致性检验，检验构造的矩阵是否与一致性矩阵有太大差别，接下来介绍一致性矩阵。

一致性检验

1.一致矩阵

下图中左侧是构造的判断矩阵，右侧是其对应的一致矩阵，如果构造的判断矩阵与一致矩阵差别太大的话则不可以使用，要重新构建判断矩阵，直至通过一致性检验为止

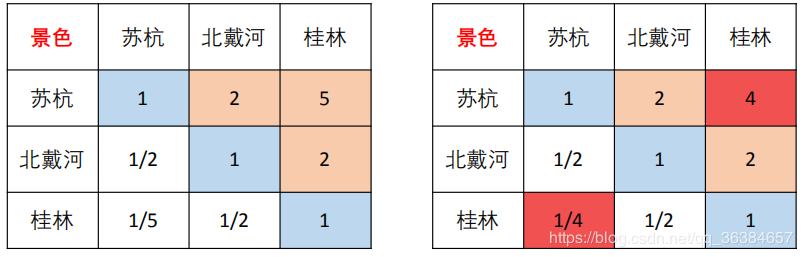
2.一致性检验的步骤

1）、计算判断矩阵最大特征值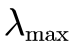、一致性指标CI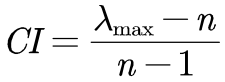

n是矩阵的维数，一致矩阵的最大特征值为n，当判断矩阵的最大特征值为n时，此判断矩阵为一致矩阵。

2）、根据n的大小，按照下表查找平均随机一致性指标RI

3）、计算一致性比例CR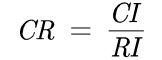


如果CR < 0.1, 则可认为判断矩阵的一致性可以接受；否则需要对判断矩阵进行修正。修正的方法是往一致矩阵上调整，（一致矩阵各行成倍数关系）。**