一、基本概念

哈弗曼树就是最优二叉树

1. 术语

1. 路径

从树当中的一个结点到另一个结点之间分支构成这两个结点之间的路径

2. 结点的路径长度

两个结点之间的路径上的分支数

3. 树的根结点长度

从树根到每个结点的路径长度之和，记作:TL
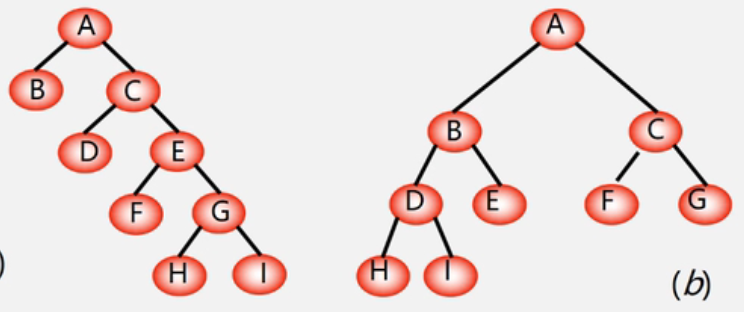
image.png

结点树木相同的二叉树中，完全二叉树是路径最短的完全二叉树

4. 权

树的结点赋予一个含有某种意义的数值，则这个数值称为为结点的权,.

5. 结点的带权路径长度

从根结点到该结点之间的长度与该结点的权乘积;

6. 树的带权路径长度

  1. 树所有叶子结点的带全路径长度之和:WPL

2. 例子

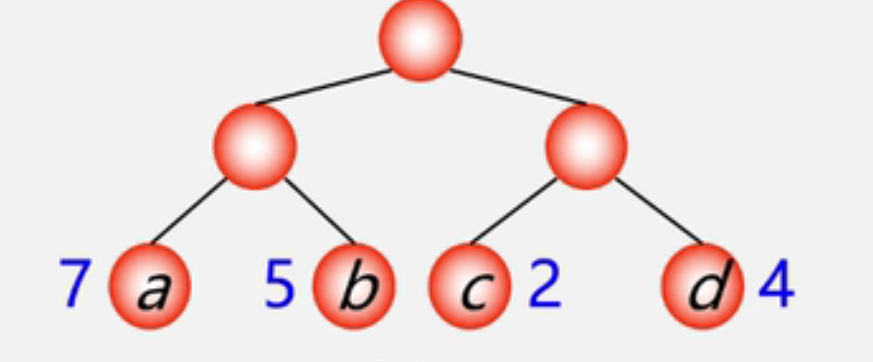
image.png

image.png
以上二叉树的带权路径是？

  • WPL = 27+25+22+24 = 36;

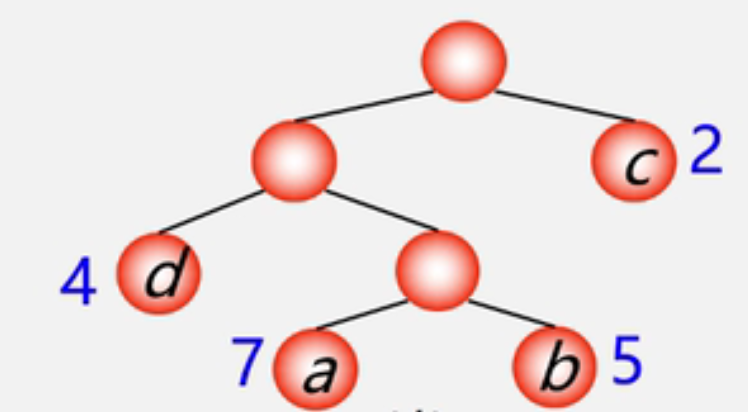
image.png
以上二叉树的带权路径长度是多少??

  • WPL = 42+37+3*5+2 = 46

小总结

  • 哈弗曼树:是带权路径WPL最短的树；要求‘度’相同；

image.png

  • 权值越大，越离根近，权值越小，离根越远。
  • 满二叉树不一定是哈弗曼树
  • 具有相同带权结点的树不一定相同。


二、哈弗曼算法

哈夫曼算法

  1. 构造森林全是根
  2. 选权值最小的树作为左右子树，构造新的二叉树，其根结点是两个左右子树上结点权值之和
    1. 选用两小造新树
  3. 删除两小添加新人。
  4. 重复2、3剩单根

    小练习

    image.png
    image.png

小总结

  1. 初始中有n个二叉树，经过n-1次合并最终行程哈弗曼树
  2. 会产生n-1新结点(度为2)和n个(度为0)的结点
  3. 哈弗曼树当中一定有2n-1个结点

三、哈弗曼树构造算法的实现

  • 采用顺序存储———一维结构数组
    1. /**
    2. 哈弗曼树 
    3. **/
    4. typedef struct {
    5.   int weight; //权
    6.   int parent,lch,rch; //孩子和双亲 
    7. }HTNode,*HuffmanTree;//可以表示数组
    image.png

算法实现(待)

  1. 初始化，出入叶子结点的权值
  2. 进行n-1次合并，一次产生n-1个结点Ht[i],
    1. ht[1,i-1]中选择parent=0的weight值最小的两个结点HT[s1]和HT[s2];
    2. 他们两个的双亲就是新结点
    3. 新结点的parent=0,lchild=s1,rchild=s2,weight=HT[s1]+HT[s2]

四、哈弗曼编码

1. 概述、