review

图概述

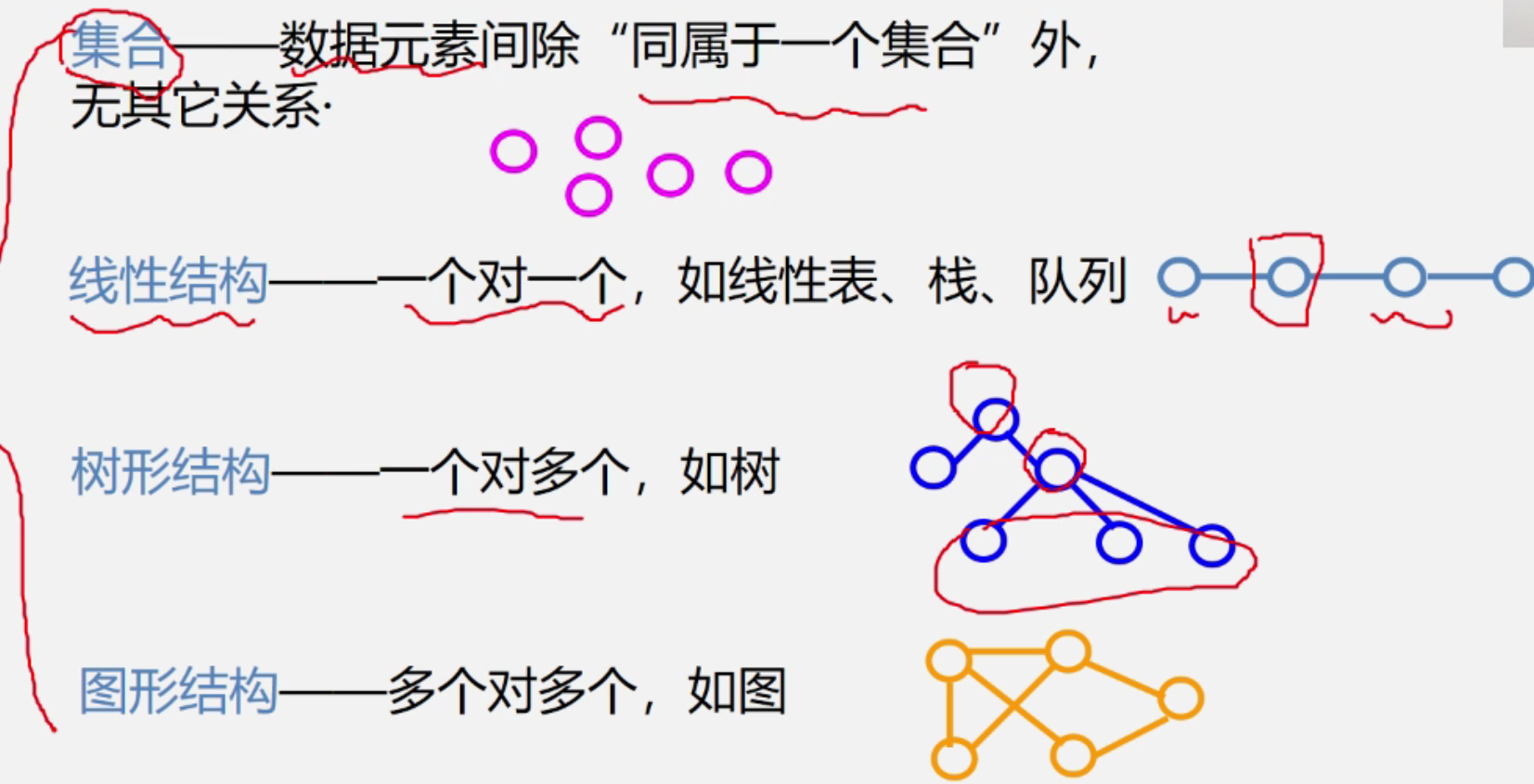
1. 图的基本概念

• v=VERTEX
• E=Edge
• 有向图: 每个边都有方向
• 无向图: 每个边都没有方向

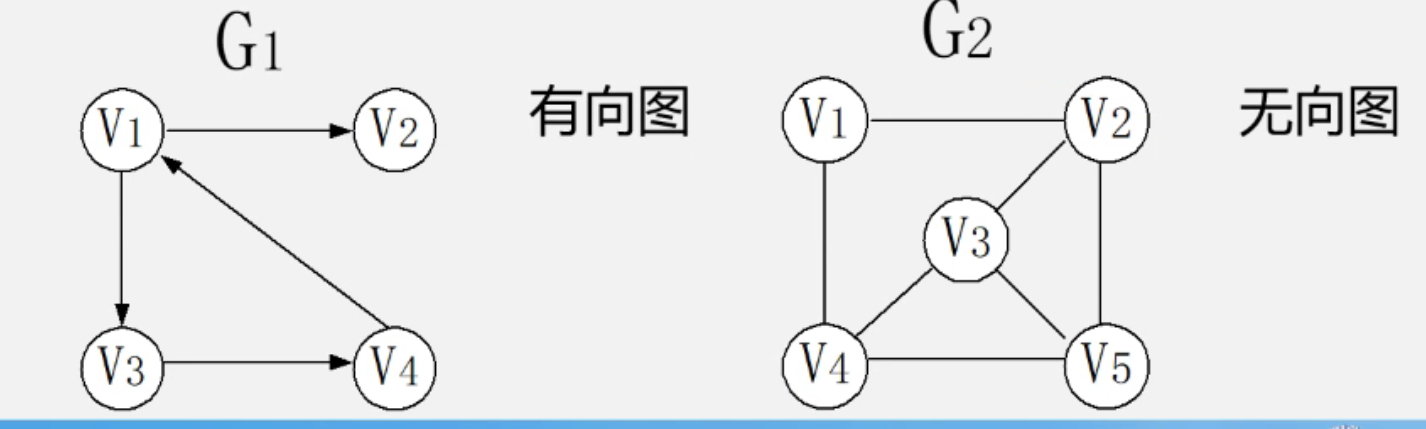
1. 完全图概念

就是任意两个顶点都有一条边相连接

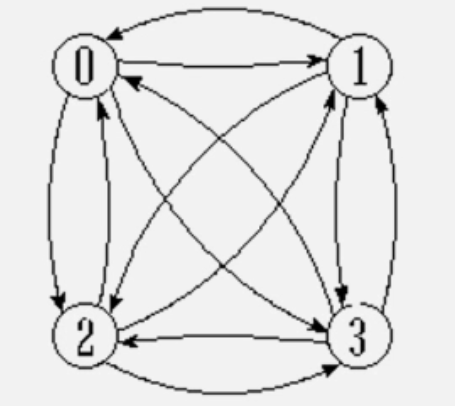
完全有向图

• 含有n个顶点，有n(n-1)条边

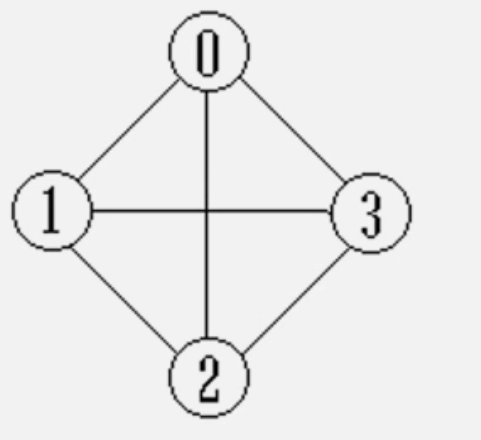
完全无向图

• n个顶点的有向完全图有 n(n-1)/2个边

2. 稀疏图

稀疏图就是有很少的边或者弧的图(e<nolgn)

3. 稠密图

有较多的边或者弧的图

4. 网**

边/弧度带权的图

5.领接

有边/弧相连的两个顶点之间的关系

• 存在(Vi,vj),则称为vi和vj是邻接点；

• 存在则成vi领接到vj，vj邻接与vi；

  6. 关联(依附)

  边\弧与顶点之间的关系。

• 存在(vi,vj)/，则说该边关联着vi和vj

  7. 顶点的度

  与该顶点相关连着的边的数目，记作(TD(v))

• 在有向图当中还分成入度和出度

• 入度:ID(v)
• 出度:OD(V)

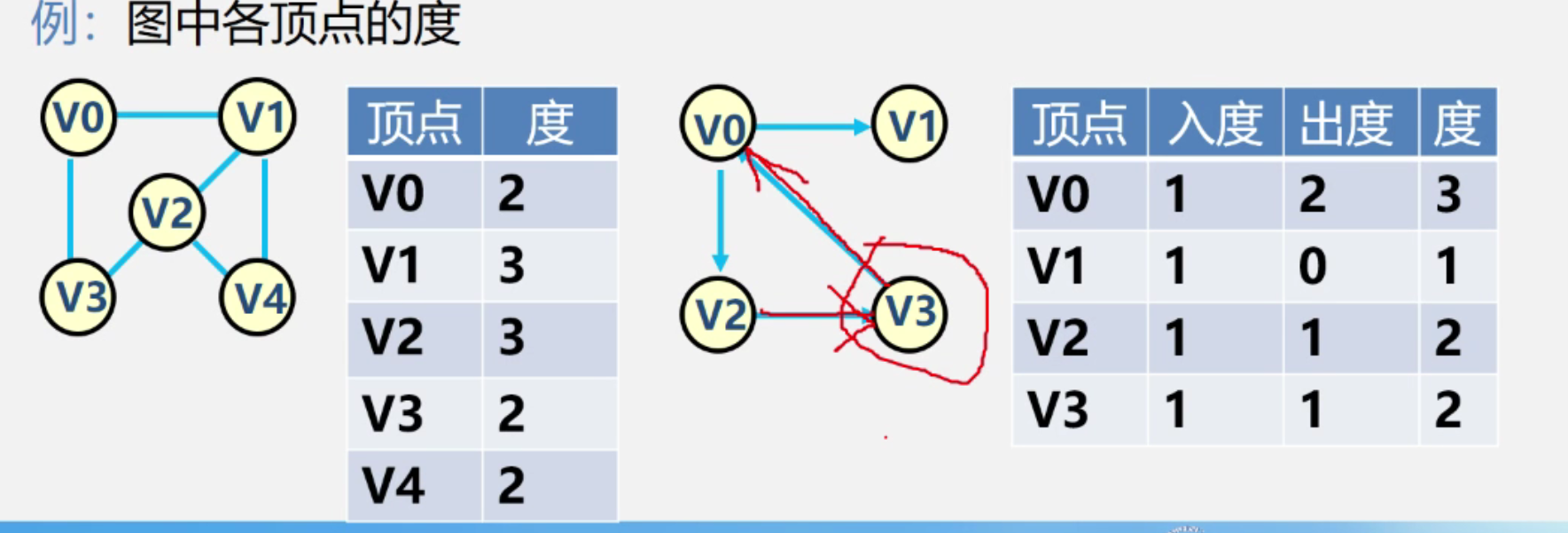
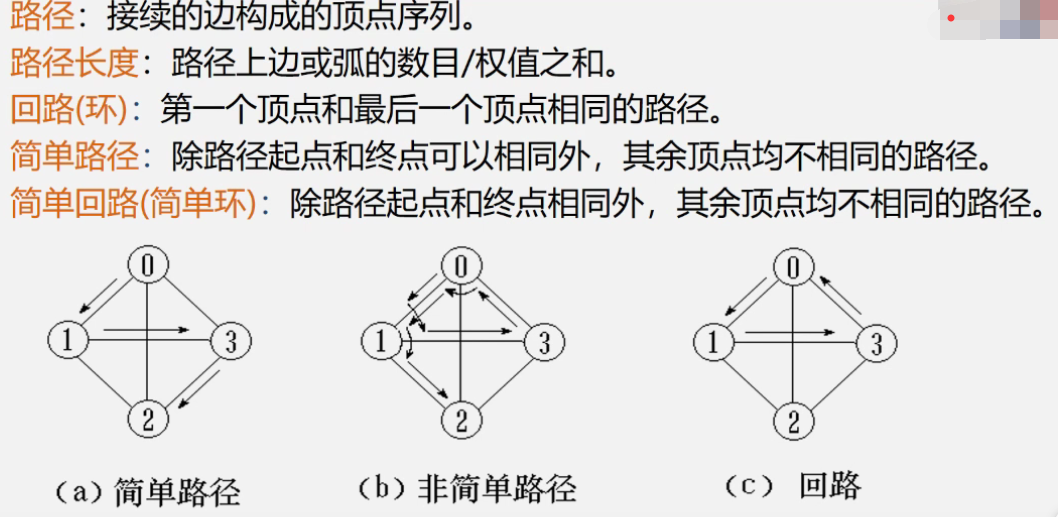
2. 图的路径

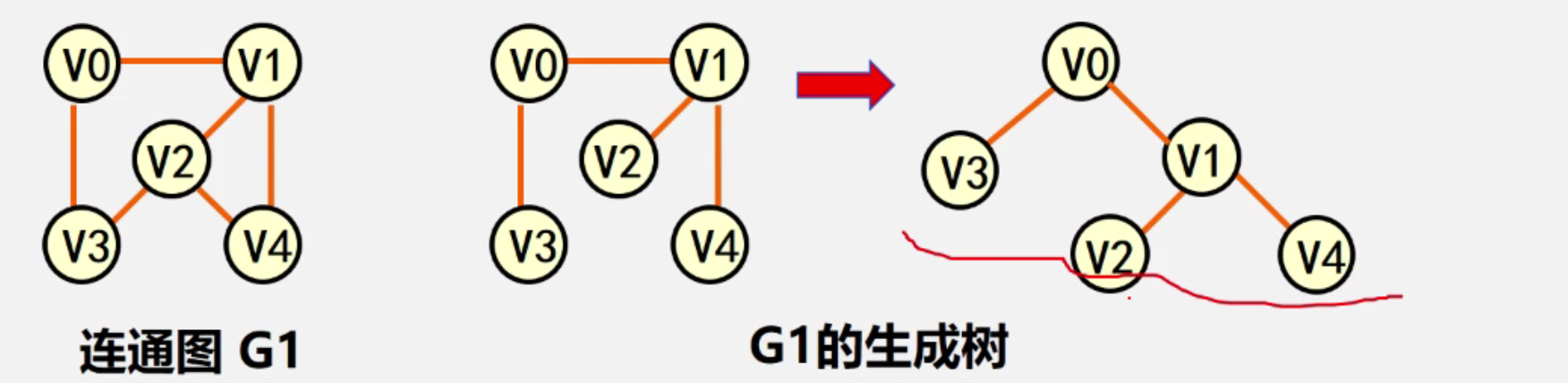
3. 连通图

在无(有)向图当中 G=(V,{E})中，任何两个顶点V u都存在v到u的路径,则称为G为连通图(强连通图).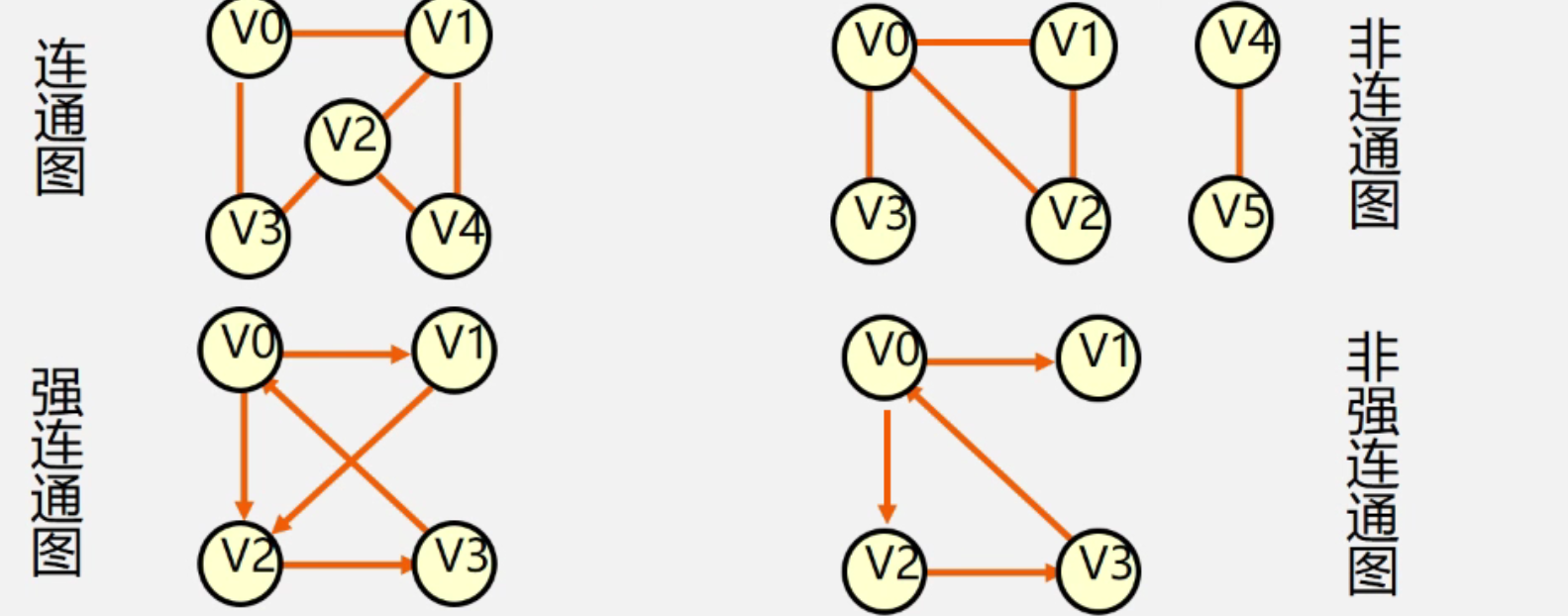

4.权和网

图中边和弧所具有的相关的数称为权，表明一个点到另一个结点的距离和耗费。

5. 子图

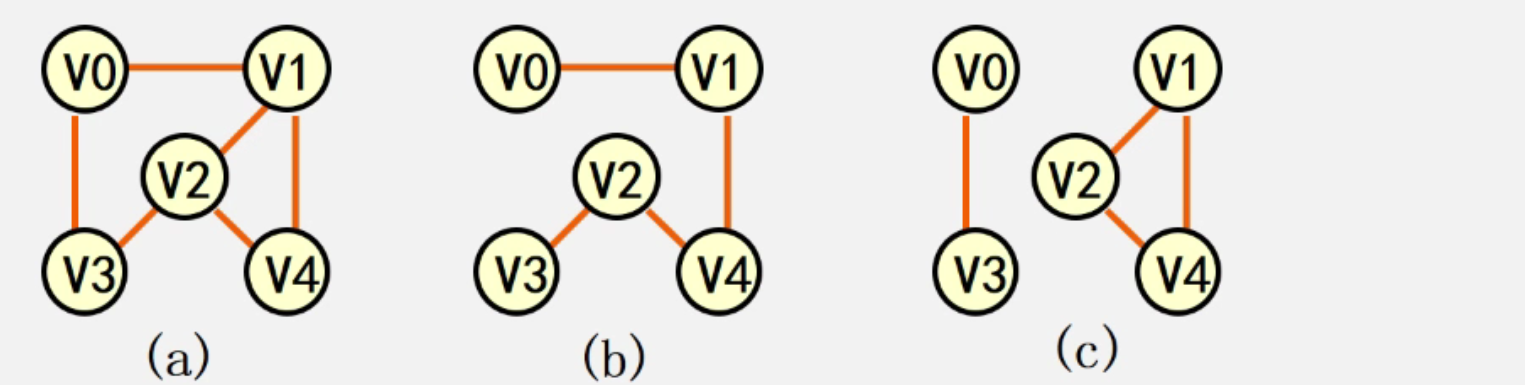
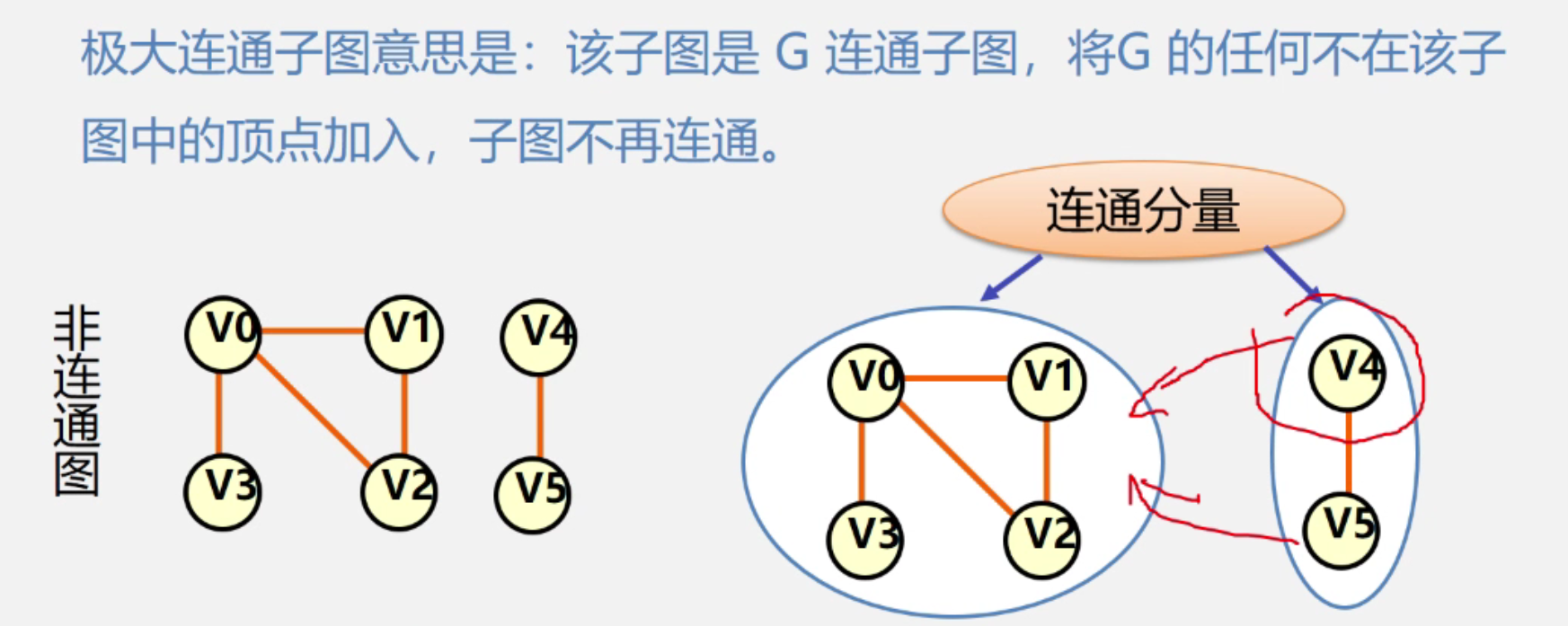
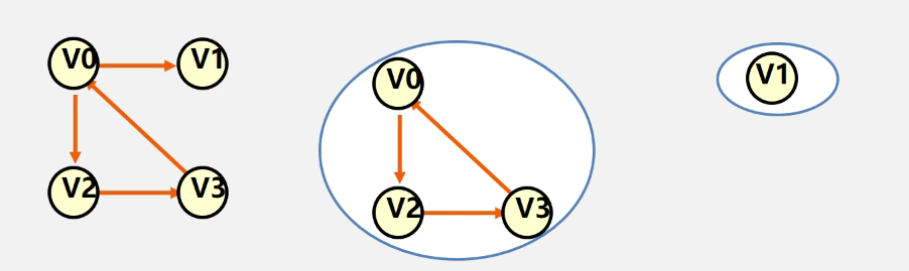
6. 连通分量(强联通分量)

• 无向图G的连通子图称为G的连通分量
• 强连通分量的也就是有向图的强连通分量

极小联通子图

• 子图是G的连通子图，删除任何一个顶点就不会在联通

  生成树

• 包含了无相图所有顶点的极小连通子图

  生成森林

• 对于非连通图，由于各个连通分量生成树的集合。