图的逻辑结构: 多对多

  • 图没有顺序存储结构
  • 可以接住二维数组来确定元素之间的关系
  • 邻接矩阵

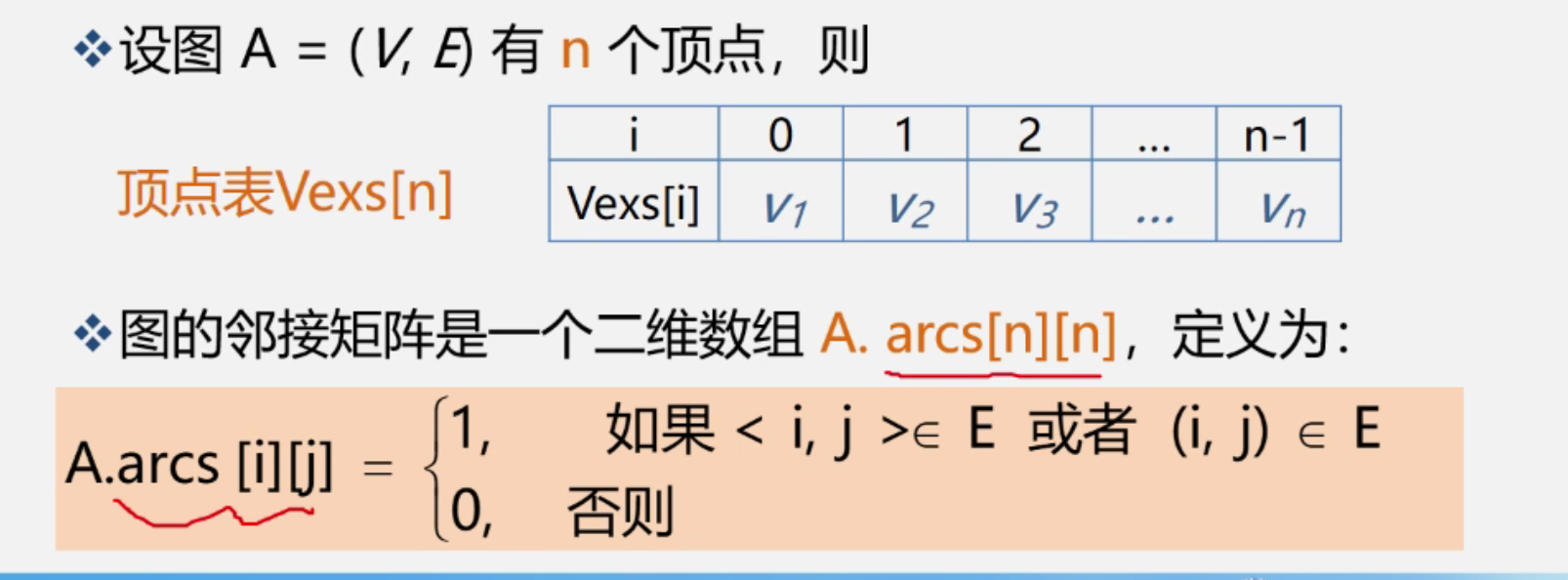
image.png

一、邻接矩阵

邻接矩阵是用数组表示法

思路

  1. 建立一个顶点表，邻接矩阵用来描述顶点的关系

image.png

例子

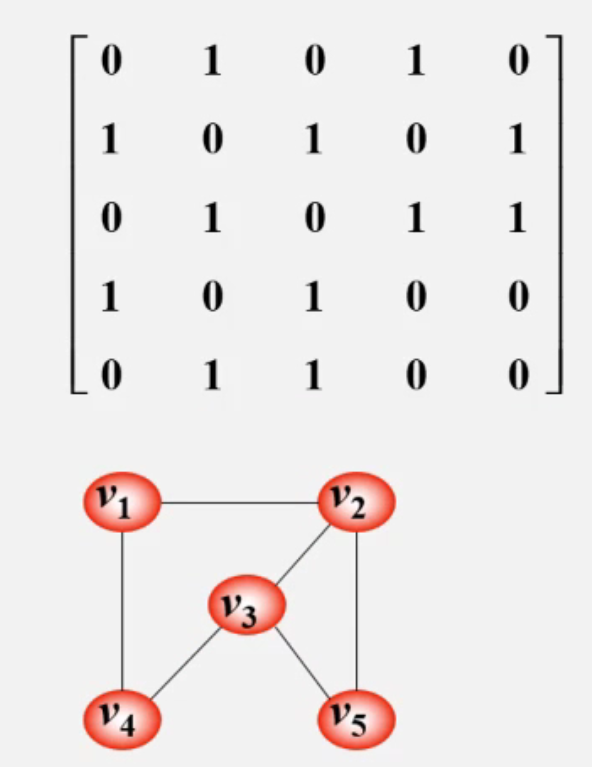
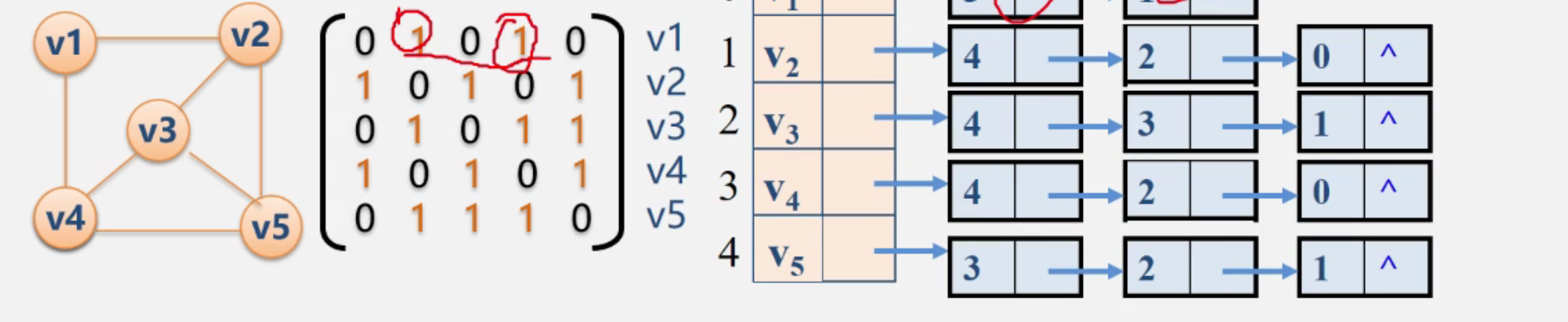
无向图 的邻接矩阵

  • 无向图的邻接矩阵是对称的
  • 顶点i的度是第i行1的个数

image.png

完全的邻接矩阵当中，对角元素为0，其余为1.

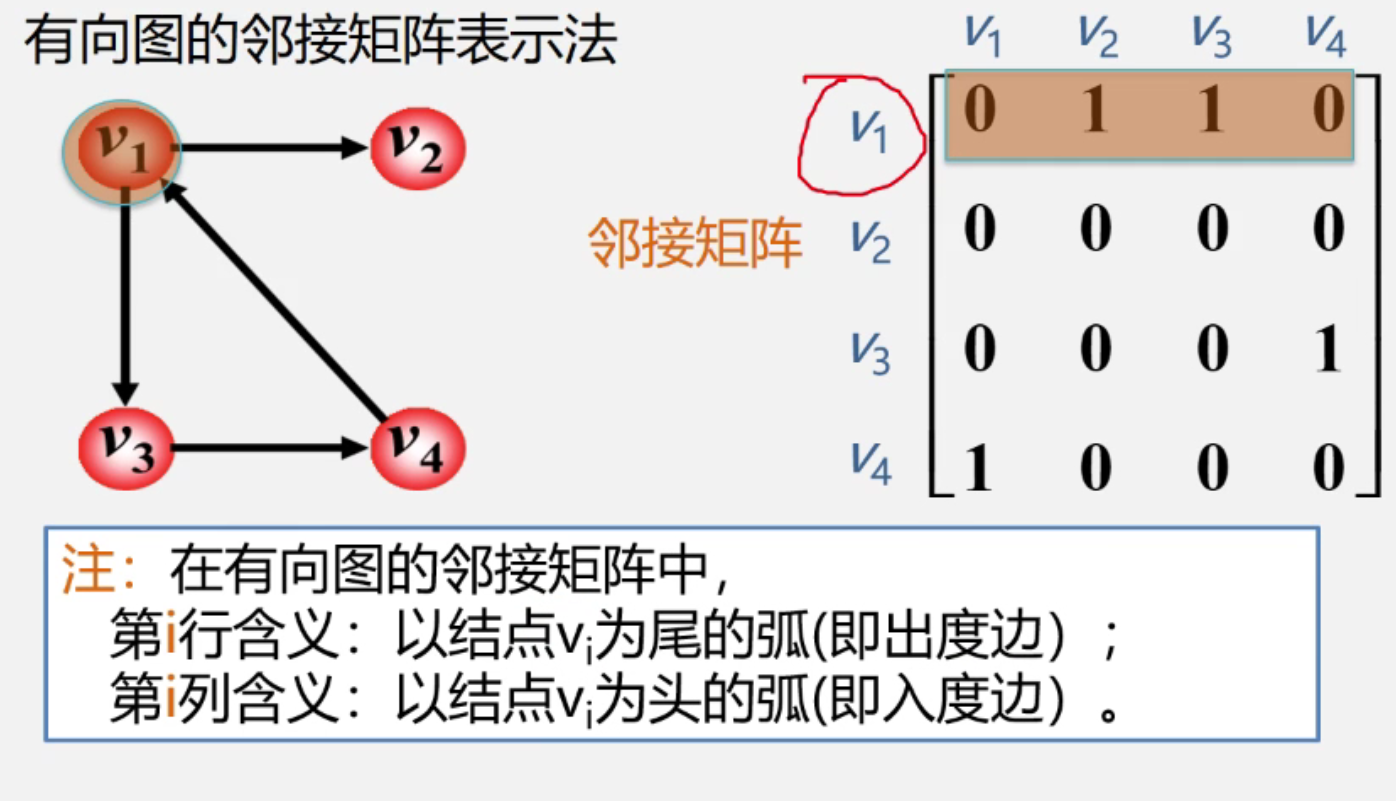
有向图的邻接矩阵

  • 行为出度边、列为入度边
  • 可能不是对称的邻接矩阵
  • 出度=第i行元素之和
  • 入度=第i列的元素之和

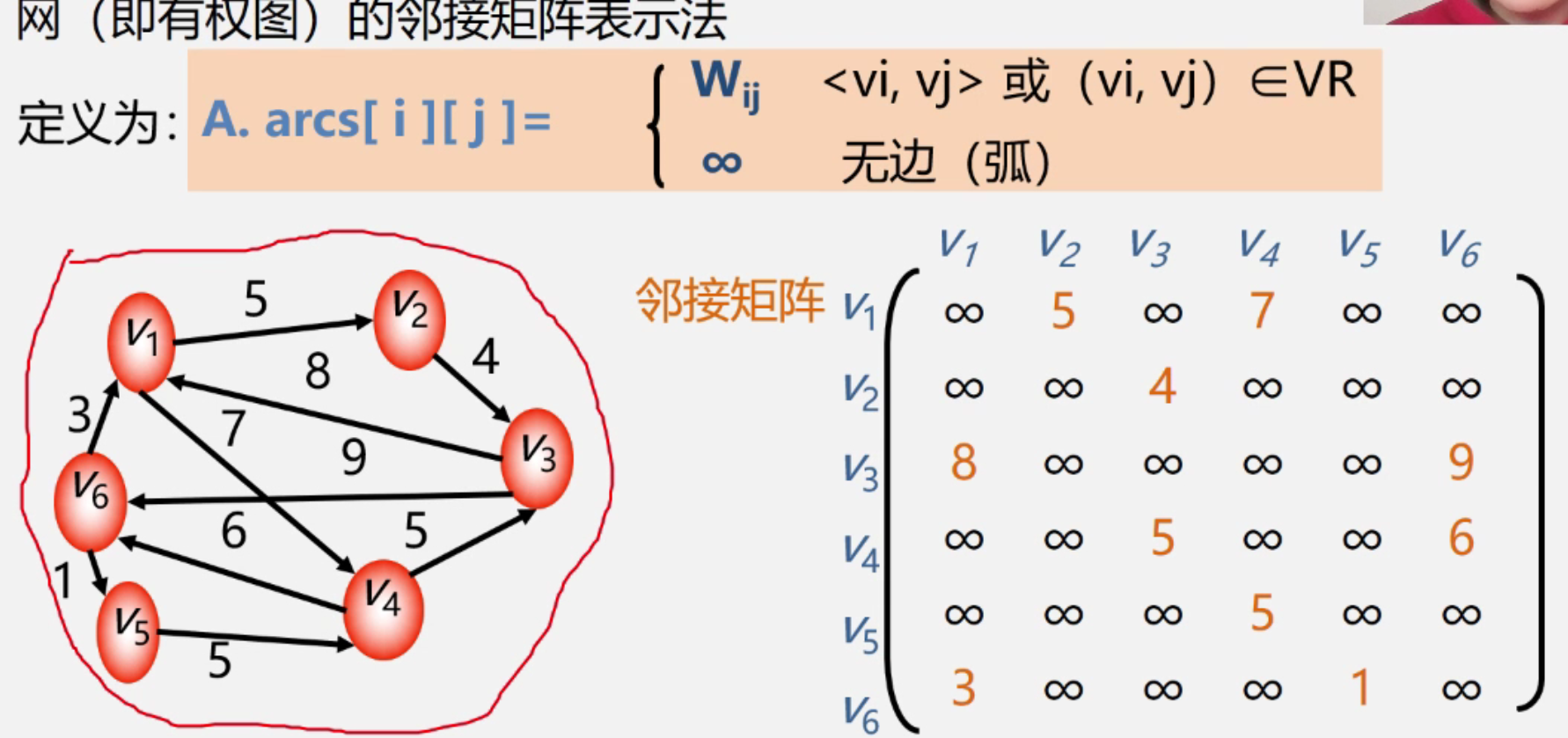
image.png

网的邻接矩阵

image.png

邻接矩阵的建立

邻接矩阵过的存储表示: 用两个数组分别存储顶点表和邻接矩阵;

1. 基本的语言定义

  1. #define MaxInt 3412324;//MaxSize of 
  2. #define MVNum 100 //最大的顶点
  3. typedef char VerTexType;
  4. typedef int ArcType; // wight is int
  5. typedef struct{
  6.     VerTexType vexs[MVNum]; //顶点表
  7.     ArcType arcs[MVNum][MVNum]; //邻接矩阵
  8.     int curVexNum,arcNum ;//arcNum and current Vex;
  9. }AMGraph;

2. 无向网的定义

  • 输入总的顶点数和总边树
  • 依次输入点的信息存储顶点表当中
  • 初始化邻接矩阵，是每个权威最大值

image.png
image.png

3. 邻接矩阵小总结

无向网转换成无向图&有向图

image.png

邻接矩阵-有什么优点？

image.png

  • 直观、简单、好理解
  • 方便检查任意顶点是否存在边
  • 方便找任意的 ‘邻接点’

  • 方便计算度!

    缺点

  • 增加和删除比较麻烦

  • 浪费空间-稀疏图: 大量无效元素
    • 对于稠密图(完全图)很合算
  • 浪费时间
    • 统计稀疏图一共有多少条边

二、邻接表

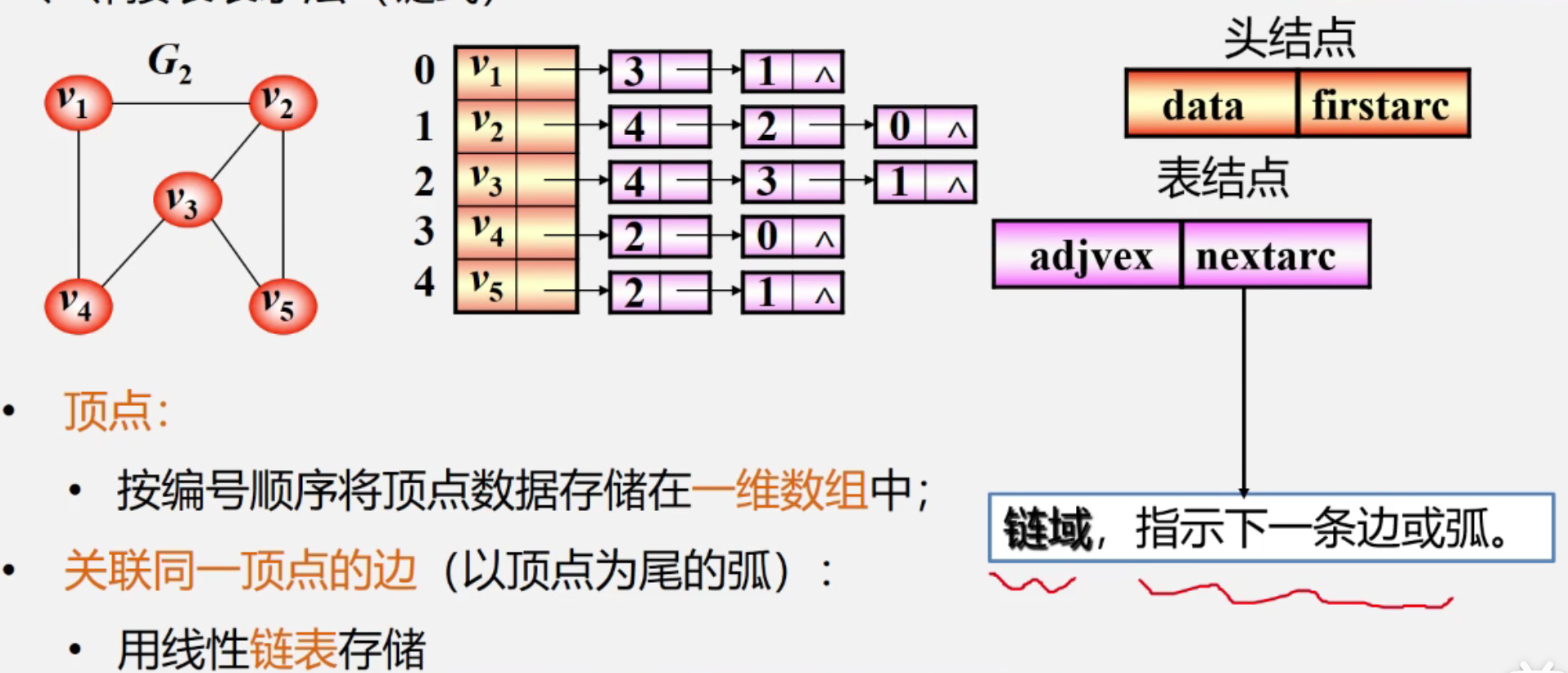
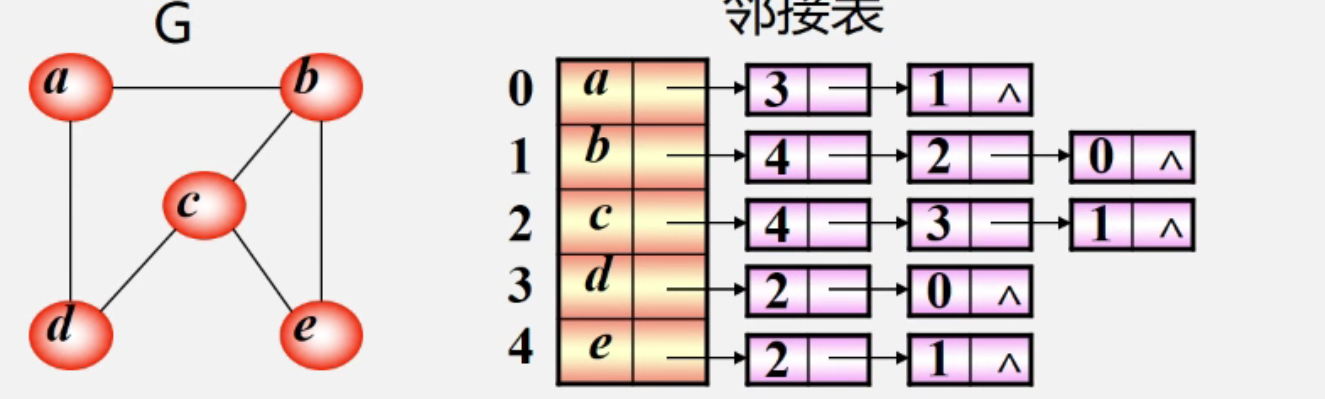
1. 无向图邻接表表示法(链)

  • 如果是一个网，可以在表结点增加一个属性

    特点

  1. 邻接表不唯一
  2. n个顶点，e条边的无向图
    1. n个头结点
    2. 2e个表结点
    3. O(n+2e)
    4. 适合用存储稀疏图
  3. vi的度是单链表当中表结点的总数
    1. 例如下图v1有度为2

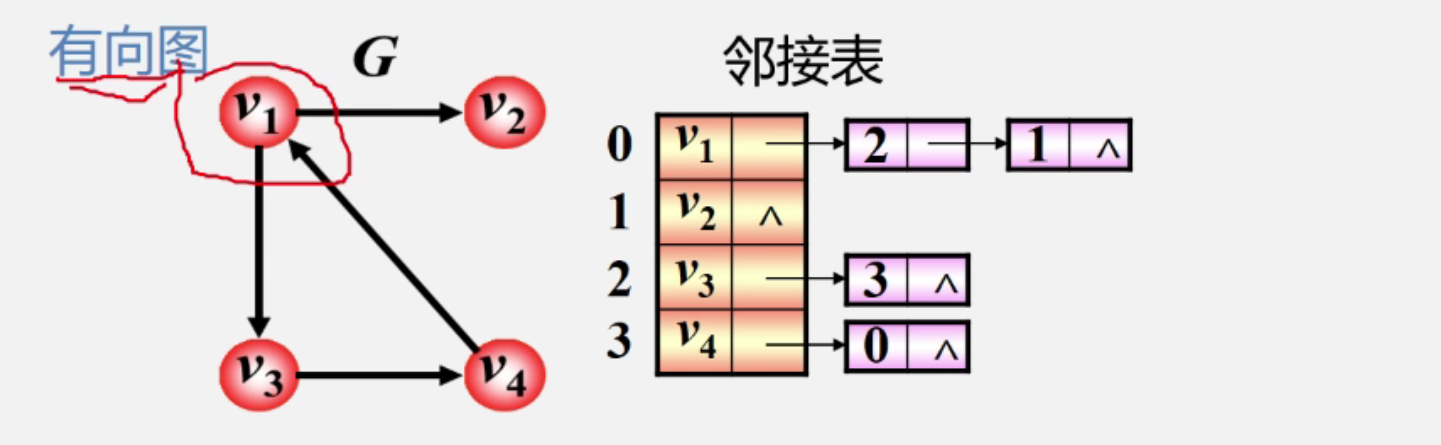
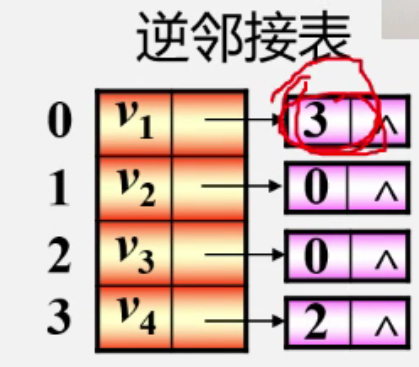
image.png

2. 有向图的邻接表

  • 只记录每个顶点的出度
  • 计算入度需要遍历整个邻接表

    特点

  1. 第vi的出度为第i个单链表的结点个数

  2. 入度为整个单链表中邻接结点域值i-1的结点个数

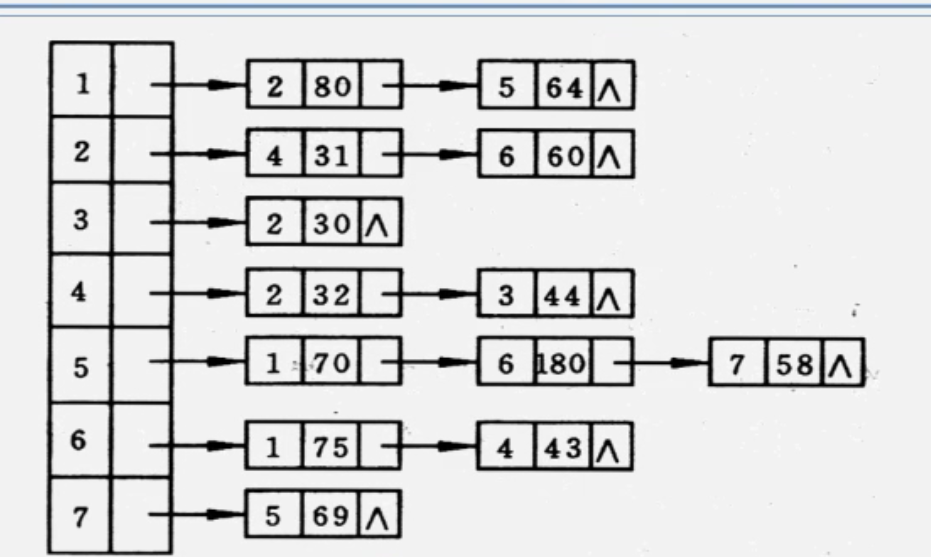
    image.png

    逆邻接点

  • 只记录入度结点

image.png

小练习

image.png

3. 邻接表的算法建立

image.png

image.png

定义

  1. #define MVNum 100
  2. //边结点结构
  3. typedef struct ArcNode{
  4.     int adjvex;//指向边所指顶点位置
  5.     struct ArcNode *ne  tarc; //指向下一条边的指针
  6.     OtherInfo info; //如果有权
  7. }ArcNode;
  9. //头结点
  10. typedef struct VNode{ 
  11.     VerTexType data; //记录顶点的信息
  12.     ArcNode *firstarc; //指向第一条依附该顶点的边的指针
  13. }VNode, AdjList[MVNum];//表示邻接表的类型
  15. typede struct{
  16.     AdjList vertices;
  17.     int vexnum,arcnum;//当前顶点数，和弧数
  18. }ALGraph;

image.png

建立算法实现

image.png

  1. Status CreateUDG(ALgraph &G){
  2.     //输入总顶点个数和边数
  4.     //输入各点、构造表头的结点表
  5.     //输入个顶点的data
  6.     //表头结点初始化
  8.     //输入各个边，构造邻接表
  9.     //一条边依附两个顶点
  10.     //生成一个边结点的空间*p1
  11.     //p1->j
  12.     //插入顶点的头部
  13.     //无向图插入两次头部   
  14. }

4. 邻接表的优缺点与邻接矩阵的关系

邻接表的特点

  • 容易找到顶点的邻接结点
  • 节约稀疏图的空间
    • 只需要n个顶点+2E个结点
  • 方便计算 ‘度’?
    • 方便无向图
    • 有向图不好计算

  • 不方便寻找任意一对顶点是否存在边

    邻接矩阵与邻接矩阵关系

    1. 联系

  • 邻接表当中的链表对应着邻接矩阵的每一行！

    2. 区别

  • 对于任意一个无向图

    • 邻接矩阵是确定切唯一的(矩阵的行列与顶点编号有关)
    • 邻接表不唯一(链表的次序与顶点编号无关)
  • 空间复杂度
    • 邻接矩阵O(n^2)
    • 邻接表O(n+e)

image.png

邻接矩阵多用于稠密图，邻接表多用途稀疏图

三、邻接表的改造与优化(略过)

在邻接表当中，对于有向图，求结点的度比较困难: 十字链表
在邻接表当中，对于无向图，每条边，都需要存储存储两边，浪费空间: 多重链表

1. 十字链表

其主要用于存储有向图，十字链表就是将邻接表和逆邻接表结合在一起，解决有向图求度困难的问题。

2. 邻接多重表