Author:JaneOnly Date: 2022.1.16 Categories: 数据结构(专升本) 本章参考王卓数据结构与算法基础
概述
排序当中应用十分广泛
- 软件当中直接应用
程序中运用
- 二分法
- 最小生成树
排序方法的分类
按照存储介质
- 内部排序: 数量不大,数据在内存当中
- 数据量大,数据在外存当中(文件排序)
- 按照比较个数
- 串行排序: 同一时刻比较一对元素
- 并行排序: 同一时刻比较多对元素
- 按照主要操作
- 比较排序: 插入、交换、选择、归并
- 基数排序: 不比较元素大小,仅仅根据元素本身取值确定有序位置
- 按照辅助空间
- 原地排序: 辅助空间为0(1);
- 非原地排序: 需要额外的存储空间
按照稳定性
- 稳定排序: 排序后相对位置不发生改变
- 非稳定排序: 排序后,相对位置发生改变
不是用来衡量排序算法优劣的
按照自然性:
- 自然排序: 输入数据越有序,排序速度越快
- 非自然排序:


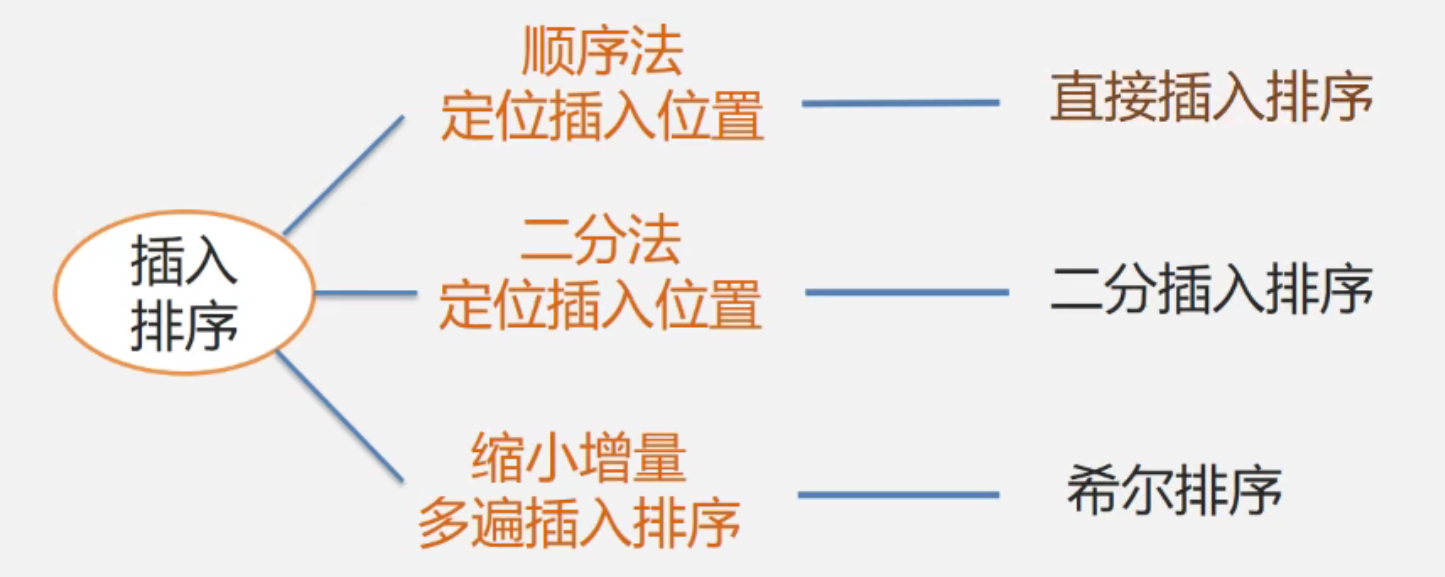
一、插入排序
基本思想
每一步将一个带排序的对象,按照其关键码的大小,插入到前面已经排好序的一组对象适当位置上,直到所有的对象全部插入为止 。
- 在有序的序列当中插入一个元素,保持序列有序,有序序列不断增加
- 在插入a[i]前
- a[0] 到 a[i-1]是有序段
- a[i] 到 a[n-1]是无序段
- 将a[i] 插入到 a[0] a[i-1]之间
- 插入到中间
- 插入到最前
- 插入到最后
- 种类
1. 直接插入排序
- 每次循环都要判断两次,浪费时间
算法实现
void InserSorct(SqList &L){int i ,j;for(i = 2;i<=L.length;i++){if(L.r[i].key < L.r[i-1].key) //若<则讲L.r[i]插入有序子表当中{L.r[0]= L.r[i]; //放置哨兵for(j = i-1;L.r[0].key<L.r[j].key;i--){L.r[j+1] = L.r[j];//往后移动}//将插入正确位置L.r[j+1].key = L.r[0];}}}
效率分析
实现排序的基本操作有两个
- 比较: 序列中两个关键字的大小
- 移动: 记录
最好的情况
- 顺序有序


最坏的情况
- 逆序有序
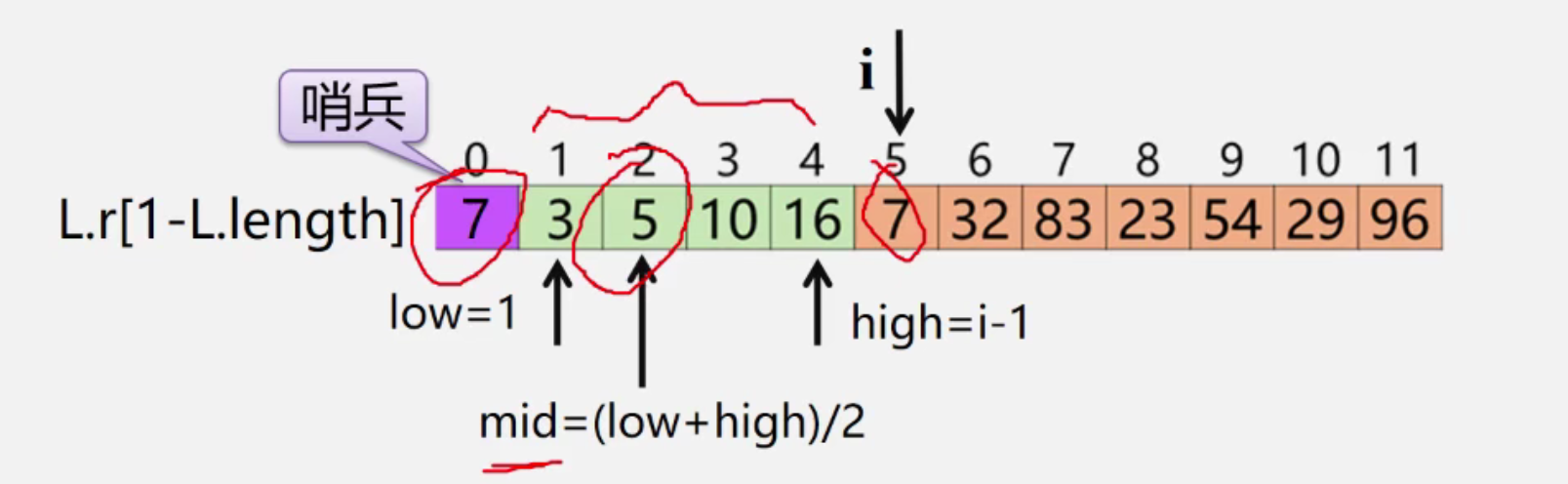
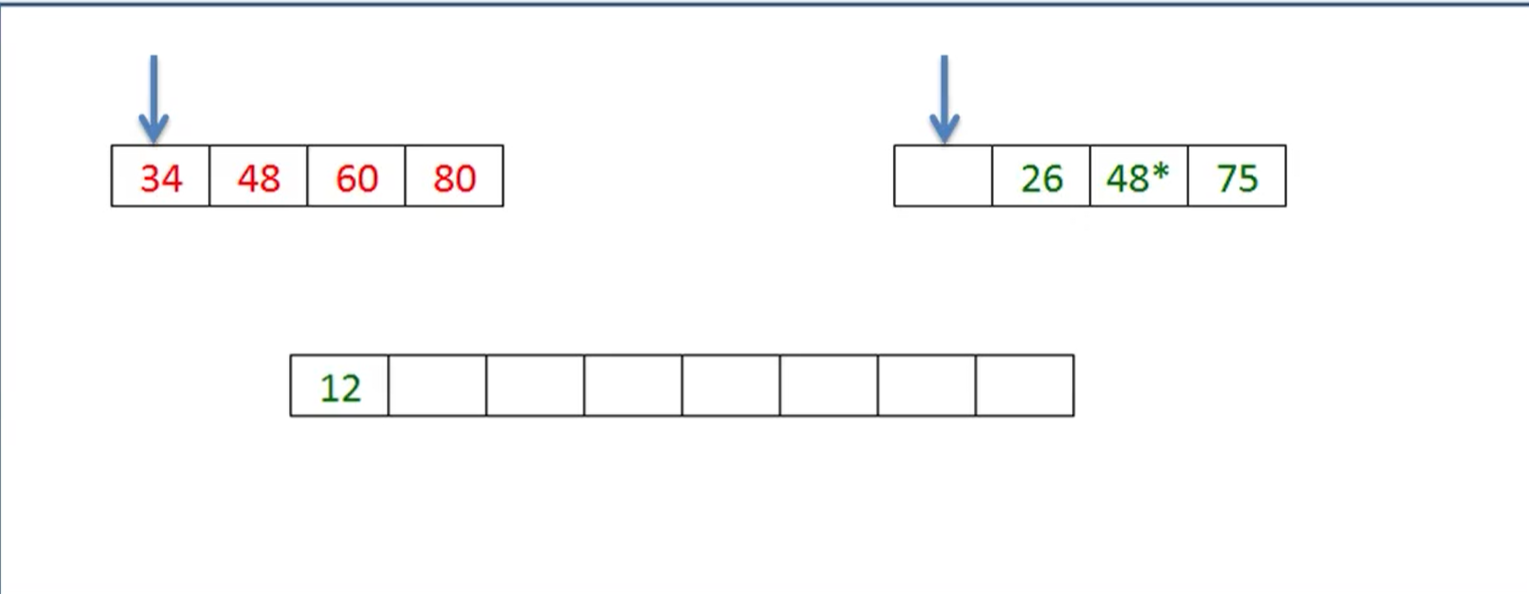
2. 折半插入排序
- 采用二分查找法,来寻找插入的位置
算法实现
void BInsertSorct(SqList &L)\{for(i = 2; i<=L.length;i++){//放置哨兵L.r[0] = L.r[i];low =1 ; high = i-1;while(low <=high){mid = (low+high)/2;if(L.r[mid].key > L.r[0].key){high = mid -1;}else{low = mid +1;}} //循环结束 high+1是要插入的值for(j = i-1;j>=high+1; --j){L.r[j+1] = l.r[j];}//插入正确位置L.r[high+1]=L.r[0];}}
算法分析
- 折半查找比顺序查找要快,所以折半插入排序比直接插入排序的平均性能更快。
比较次数和待排序的对象序列无关,仅仅是依赖对象的个数
- 插入第i个对象,需要经过 log2i(取地板值) +1
在n比较大的时候,关键码的比较次数比直接插入最坏的情况好很多,比直接插入排序最好的情况坏很多
- 插入第i个对象,需要经过 log2i(取地板值) +1
移动次数和直接插入排序相同
- 减少了比较次数,没有减少移动次数
- 平均性能由于插入排序

3. 希尔排序
直接插入排序和折半查找排序,都在移动次数上很浪费时间,那么我们可以增大移动的不服,比较一次,移动一步,到比较一次,移动一大步! 这就是希尔排序算法的思想出发点。
基本思想
先将整个带排序的记录序列分割成若干个子序列,分别进行直接插入排序,待整个序列中的记录“基本有序”时,对整体全体记录再进行一次直接插入排序。
- 缩小增量
- 多遍插入排序
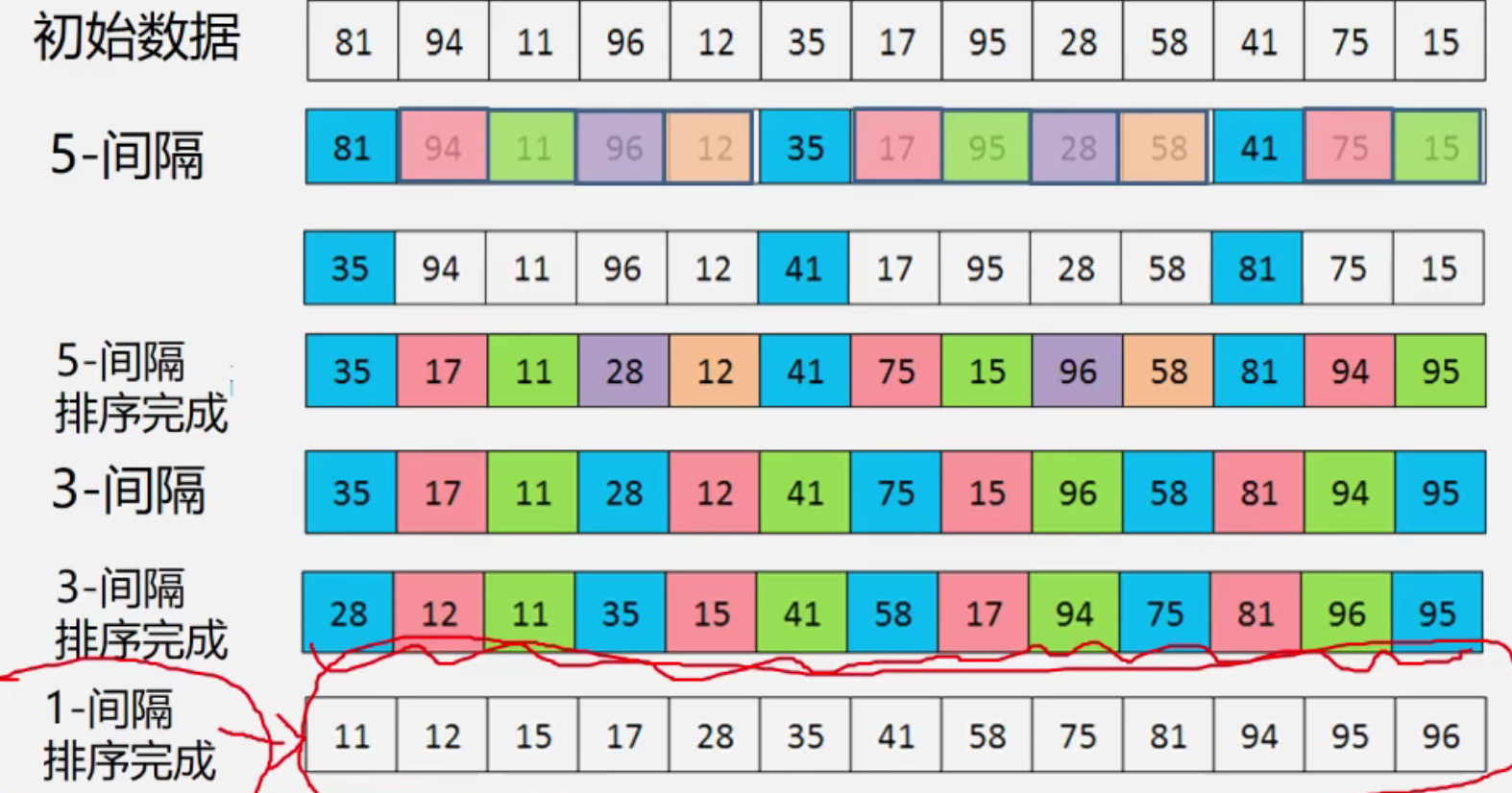
- 定义增量序列
- 对每个增量进行 Dk-间隔的插入排序.

算法实现
void ShellSort(SqList &L ,int dlta[],int t){//按照增量序列dlta[0..t-1]对顺序表L作为希尔排序for(k = 0;k<t;k++){ShellInsert(L,dlta[k]); //一趟增量为dlta[k]的插入排序}}void ShellInsert(SqList &L,int dk){for(i = dk+1;i<=L.length:i++){if(L.[i].key < r.[i-dk].key){r[0] = r[i] ;//放置哨兵for(j=i-dk;j>0 &&(r[0].key<r[j].key);j=j-dk)r[j+dk] = r[j];r[j+dk] = r[0];}}}
算法分析


增量序列如何取为最佳??尚未解决 最后一个增量必须为1,无除了1之外的公因子
不适合在链式存储中使用
二、交换排序
基本思想
两两比较,如果发生逆序则交换,知道所有的记录都排好序为止。
常见的交换排序有两种
1. 冒泡排序
基于交换排序的简单思想,每一趟不断将记录两两比较,并且按照前大后小的规则进行交换
冒泡排序
void BubbleSorct(SqList &L){int i,j, RedType temp;for(i = 0;i<n-1;i++){for(j = 0;j<n-m;j++){if(L.r[j].key > L.r[j+1].key)//发生逆序{temp = L.r[j];L.r[j] = L.r[j+1];L.r[j+1] = temp;}}}}//优化算法void BubbleSort(SqList &L){int i,j; RedType temp;int flag =1; //交换印记for(i = 0;i<n-1&&flag==1;i++){flag = 0;for(j = 0;j<n-m;j++){if(L.r[j].key > L.r[j+1].key)//发生逆序{flag = 1;temp = L.r[j];L.r[j] = L.r[j+1];L.r[j+1] = temp;}}}}
性能分析
最好的情况(正序)
- 比较n-1次
移动0次
最坏的情况(逆序)
比较次数
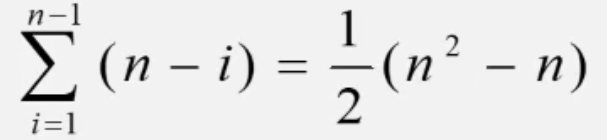
- 移动次数
- 平均为O(n2)
- 需要临时辅助空间O(1)
- 稳定排序

2. 快速排序
基本思想
- 任意选取一个元素为中心
- 比中心小的在左边,大的在右边
- 形成两个子表
- 对各个子表重新选择中心调整
- 直到每个子表元素只剩余一个
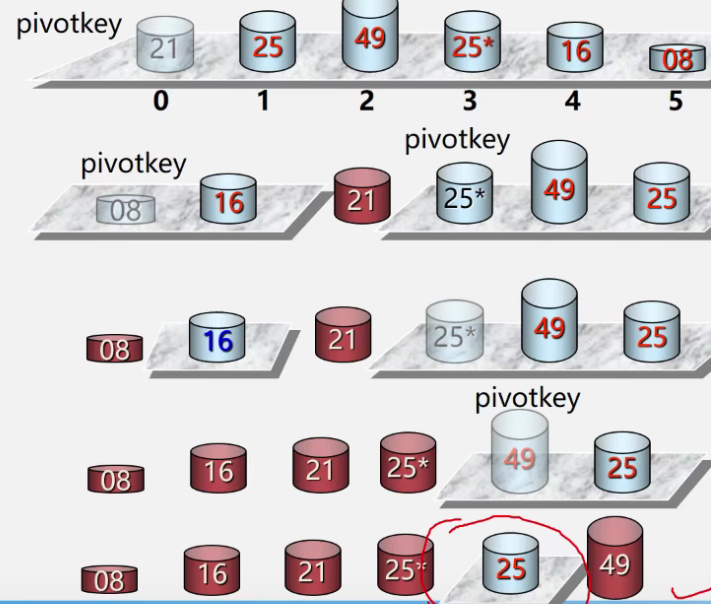
算法实现
void main(){QSort(L,1,L.length);}void QSort(SqlList &L,int low,int high){if(low<high){pivotloc = Partion(L,low,high);QSort(L,low,pivotloc-1);QSort(L,pivotloc+1,high);}}//对表进行快速排序int Partion(SqList &L,low,high){//放置哨兵L.r[0] = L.r[low];pivotkey = L.r[low].key;while(low <high){while(low<high && L.r[high].key >= pivotkey) --high;L.r[low] = L.r[high];while(Low<high &&L.r[low].key <= pivotkey) ++low;L.r[high] = L.r[low];}L.r[low] = L.r[0];return low;}
性能分析
- 快速排序不是使用与原本有序和基本有序的记录进行排序。

算法实现
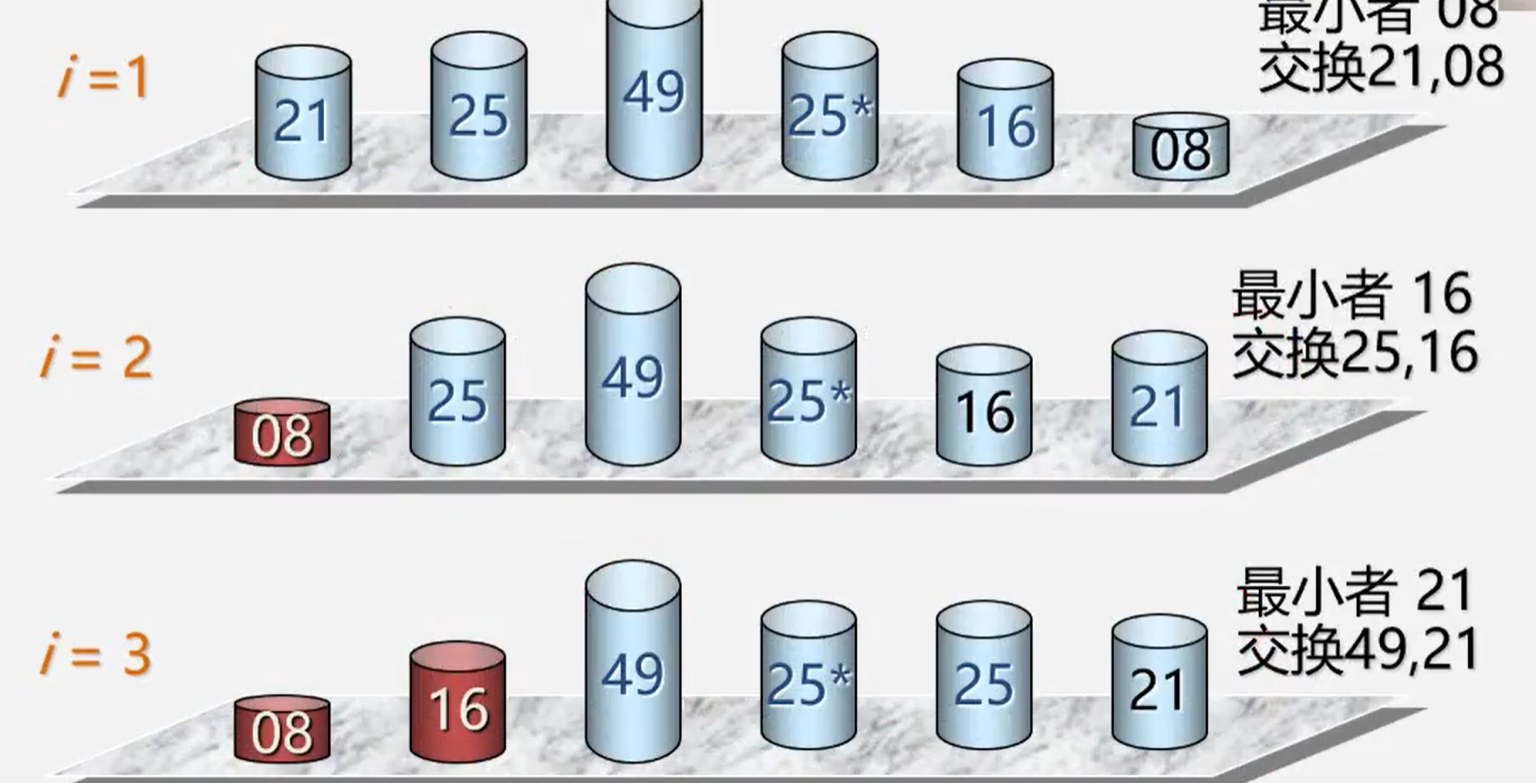
void SelctSort(SqList L ,SqlList &K){for(int i =1;i<L.length;i++){k= i;}for(int j <u+1;j<=L.length;i++){if(L.r[j].key <L.r[k].key) k= j; //记录最小值的位置}if(k!=i); L.r[i]<--<L.r[k]; //交换}
性能分析

堆的调整
小根堆
- 输出堆顶元素,使用堆的最后一个元素替代
- 然后将根结点和左右子树的根结点进行比较,并且其中最小的进行交换
- 重复上面的操作,直到是叶子结点,将得到新的堆,从堆顶到叶子的调整过程为 “筛选”;
大根堆也是同理

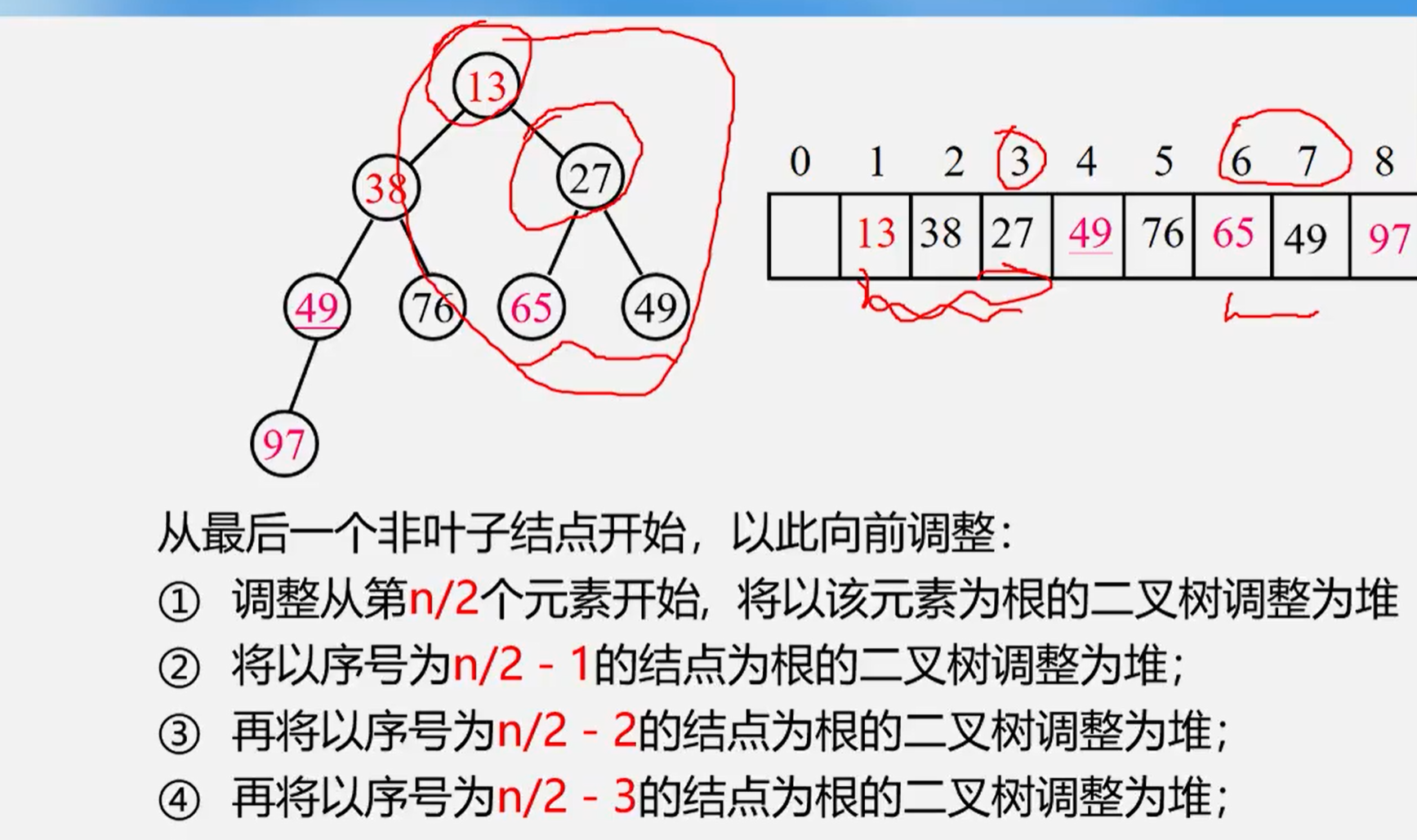
对于一个无序的序列反复筛选,就可以得到一个堆,怎么样从无序序列建立成一个堆??
堆的建立

-
建立步骤
排序的实现
算法分析
算法时间复杂度 O(nlogn)
- 最好或者最坏的复杂度O(nlogn)
- 空间复杂度 O(1)
- 非稳定排序
- 适合与n比较大的情况
四、归并排序
基本思想:
将两个或者以上的有序子序列 归并成一个有序的子序列;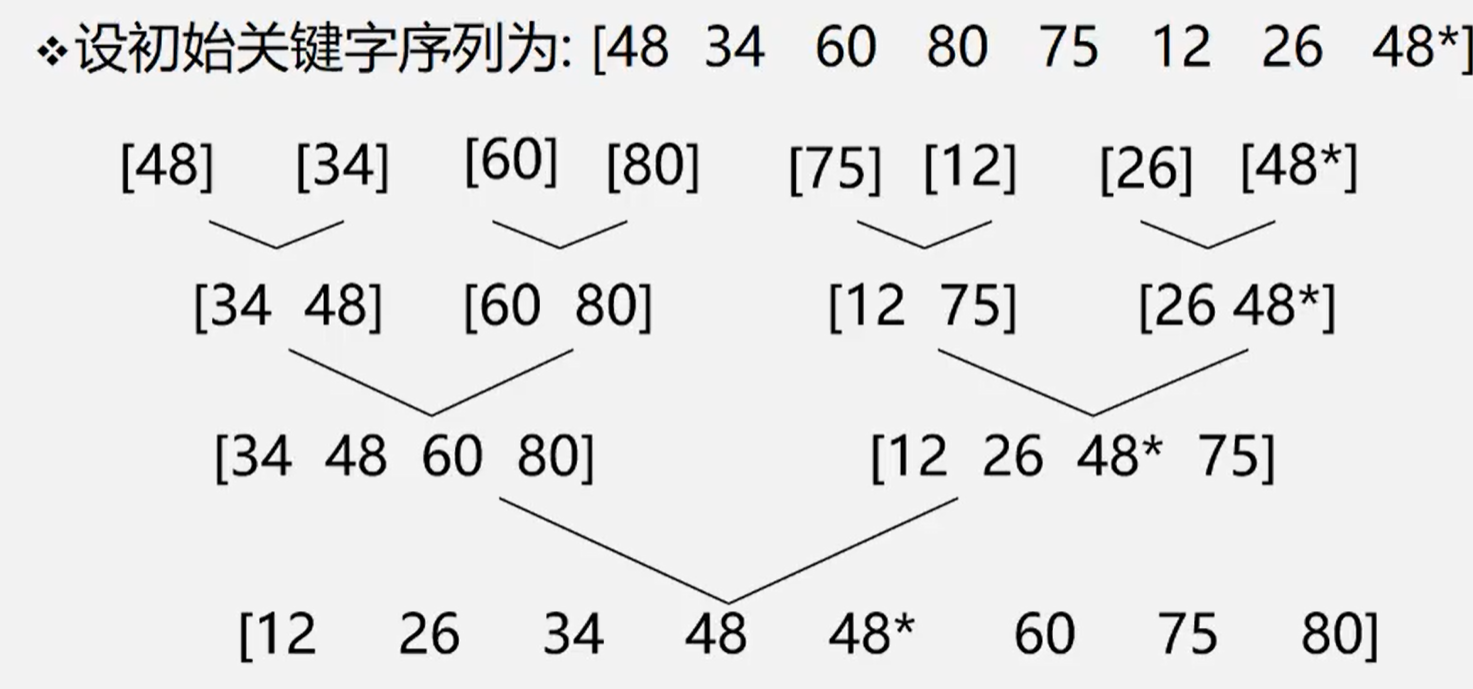
算法分析

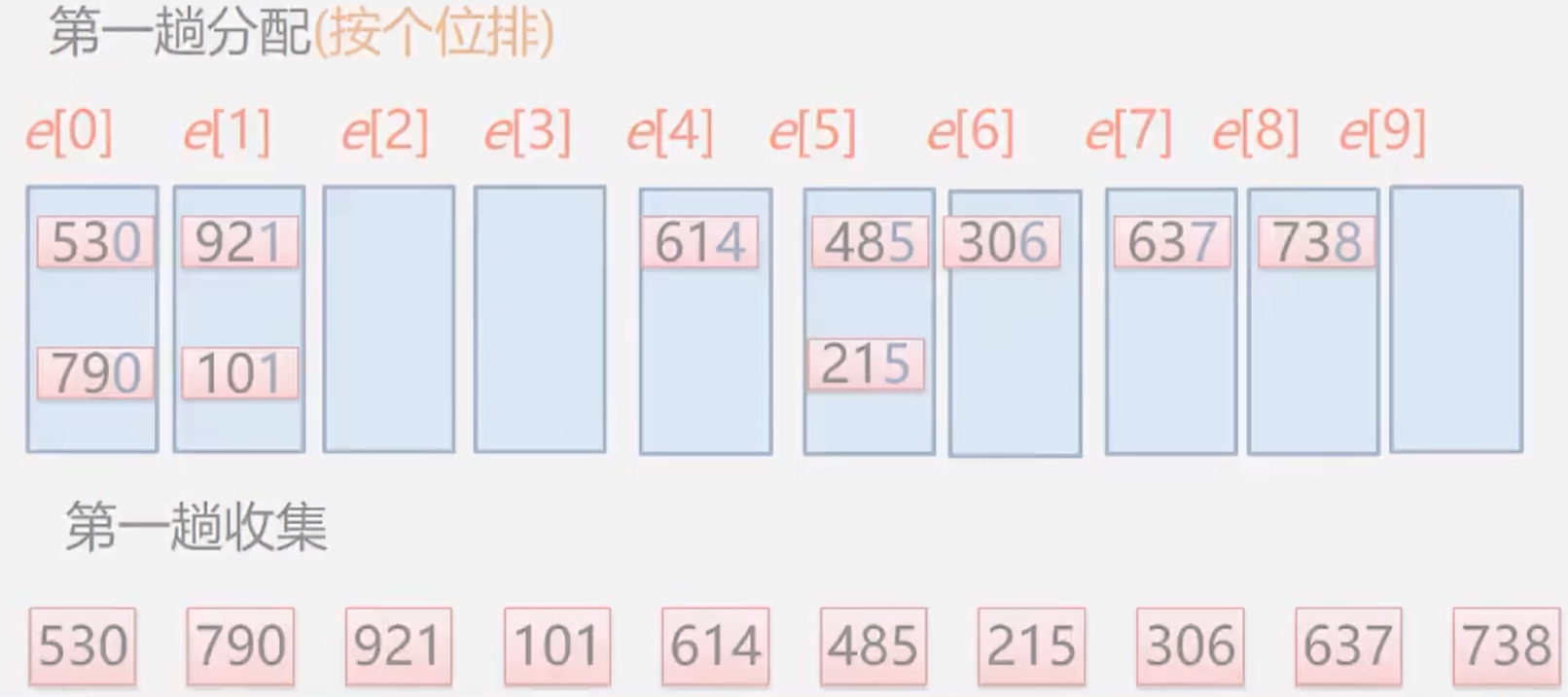
五、基数排序
基本思想
分配+收集
也叫桶排序:设关键字为K的记录放入到第K个箱子,然后按照序号将非空的连接
实例



算法分析
小总结