Author:JaneOnly300 Date:2021：12.6 Categories: 数据结构(专升本) 本章参考王卓数据结构与算法基础

一、基本概念

1. 在哪查找？

  • 可以存成线性表
  • 可以存成树表
  • 可以存成哈希表

image.png

2. 什么是查找？

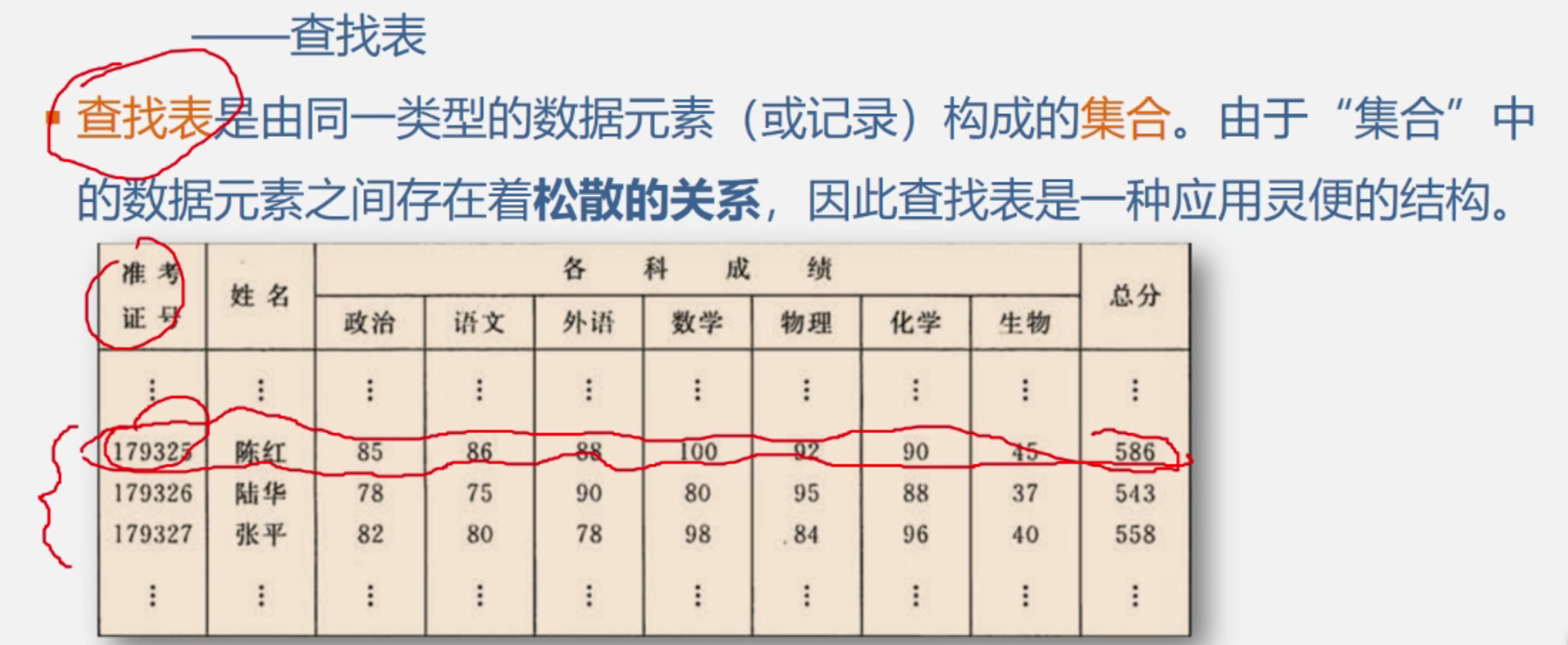
根据给定的某个值，在查找表中有关键字等于给定的值

术语

  • 关键字:用于标识一个数据元素(记录)的某个数据项
    • 主关键字
      • 唯一标识一个记录的
    • 次关键字
      • 用于识别若干记录的关键字

        查找目的?

  1. 查询特定的数据元素是否在查找表中
  2. 检索某个特定数据元素的各种属性
  3. 插入一个数据元素
  4. 删除某个数据元素

    3. 查找表分类

    静态查找

  • 仅仅查找，不对表进行插入删除操作

    动态查找

  • 查找之后，对该查找表进行删除，添加，或者修改操作

    4. ASL平均查找长度

    就是关键字平均比较的次数，也称之为平均查找长度。
    image.png

查找的方法取决于查找表的数据结构，终点研究提高查找表的查找效率;

二、线性表的查找

1. 顺序查找

应用范围

  • 顺序表活线性表表示的静态查找表
  • 表内元素无序

    数据元素类型定义

    ```c typedef struct{ KeyType key ;//关键字 … }ElemType;

typedef struct{ ElemType *R;//表的基地址 int length; }SSTable; SStable ST;// 定义顺序表

  1. <a name="yh8qB"></a>
  2. ###  算法实现
  3.   顺序表的0位置不存储东西。<br />![image.png](https://cdn.nlark.com/yuque/0/2021/png/12423141/1640868477477-e402b12d-a144-4df7-98fe-60ca05456364.png#clientId=u3f1ab6d7-5a80-4&from=paste&height=50&id=u985c1d67&margin=%5Bobject%20Object%5D&name=image.png&originHeight=100&originWidth=986&originalType=binary&ratio=1&size=158724&status=done&style=none&taskId=u08adc328-f845-4a05-a5dc-cc8dece5c30&width=493)
  4. ```c
  5. int Seach_Seq(SSTable ST,keyType key){
  6.     //若成功返回其位置信息，否则返回0
  7.     for(i = ST.length; i>=1;--i){
  8.         if(ST.R[i].key == key){ 
  9.             return i
  10.         }; 
  11.         return 0;
  12.     }
  13. }
  15. //每次循环只需要查找依次
  16. int Search_Se2(SSTable ST,KeyType key){
  17.     //将监视哨放在表头，这样做无需再考虑越界的问题
  18.     ST.R[0].key = key;
  19.     for(i = ST.length; ST.R[i].key !=key;--i);
  20.     if(i>0)return i;
  21.     else return 0;
  22. }

如果数组长度比较大，那么少说提高一般的效率

  • 时间效率分析
    • 如果查找第i个,需要比较n-i+1次
    • 查找失败则需要比较n+1次
  • 性能分析O(n)
    • 平均查找为(n+1)/2次

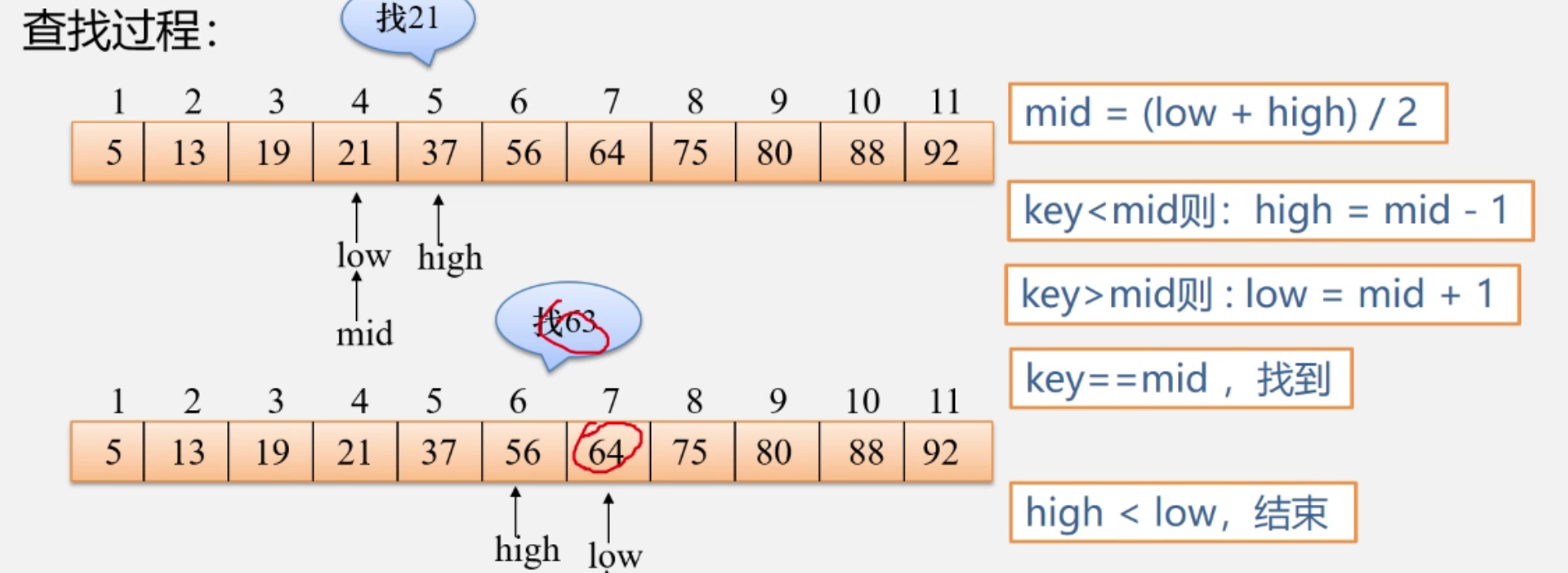
image.png

2. 折半查找(二分法)

二分查找法的前提是，找的元素一定要经过从小到大排序

  • 每次把等待查找的记录缩小一半

image.png

非递归实现

  1. int Search_Bi(SSTable ST,KeyType key)
  2. {
  3.     //初始化low,high
  4.        low = 1, high = ST.length;
  5.     while(low<= high)
  6.     {
  7.         mid = (low+high)/2;
  8.         if(ST.R[mid].key == key)
  9.         {
  10.             return mid;
  11.         }
  12.         else if (key <ST.R[mid])
  13.         {
  14.             high = mid-1; //在前半区寻找
  15.         }else
  16.         {
  17.             low = mid+1; //在右半区寻找
  18.         }
  19.     }
  21.     return 0;
  23. }

递归算法

  1. int Search_bi(SSTable ST,keyType key,int low,int high)
  2. {
  3.     if(low>high) return 0;
  4.     int mid = (low+high)/2;
  5.     if(ST.R[mid].key == key) return mid ;
  6.     else if (ST.R[mid].key >key)
  7.     {
  8.         high = mid -1;
  9.         Search_bi(ST,ket,low,high);
  10.     }else {
  11.         low = mid+1;
  12.         Search_bi(ST,key,low,high);
  13.     }
  15. }

二分法查找的前提条件是一定要经过从小到大的排序

性能分析

判定树

  • 比较次数 = 路径上的结点树
  • 比较次数 = 结点的层树
  • 比较次数 <= 树的深度

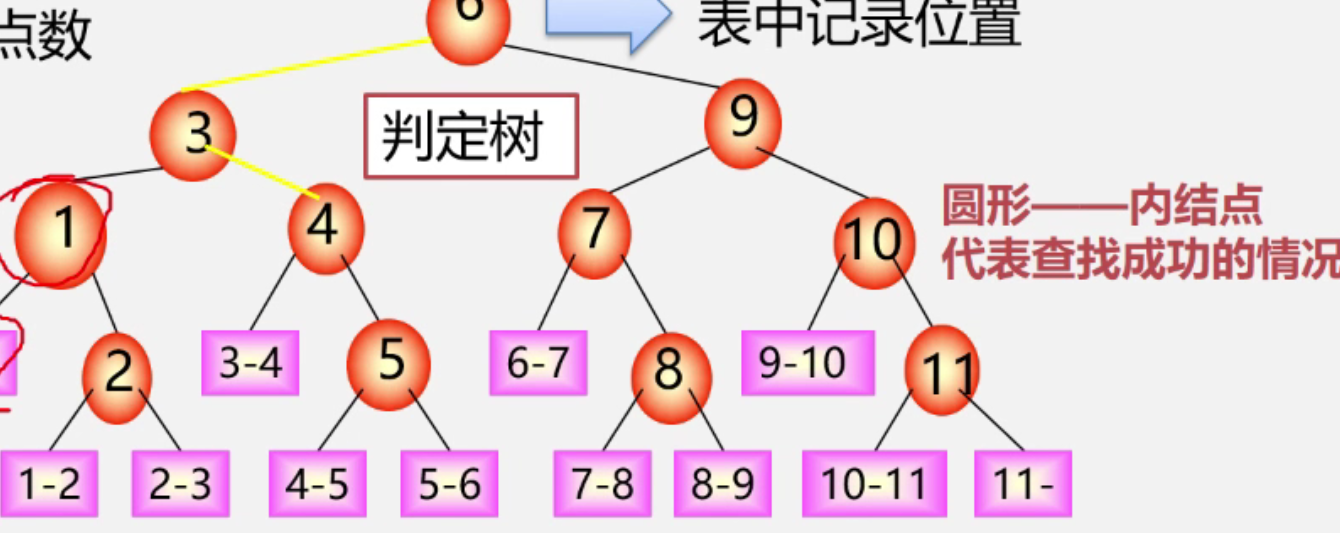
image.png

效率比顺序查找要高。 只适合用于有序表，且先至于顺序存储结构。

3. 分块查找

条件: 1. 将表分成几块，且表或者有序，或者分块有序
若 i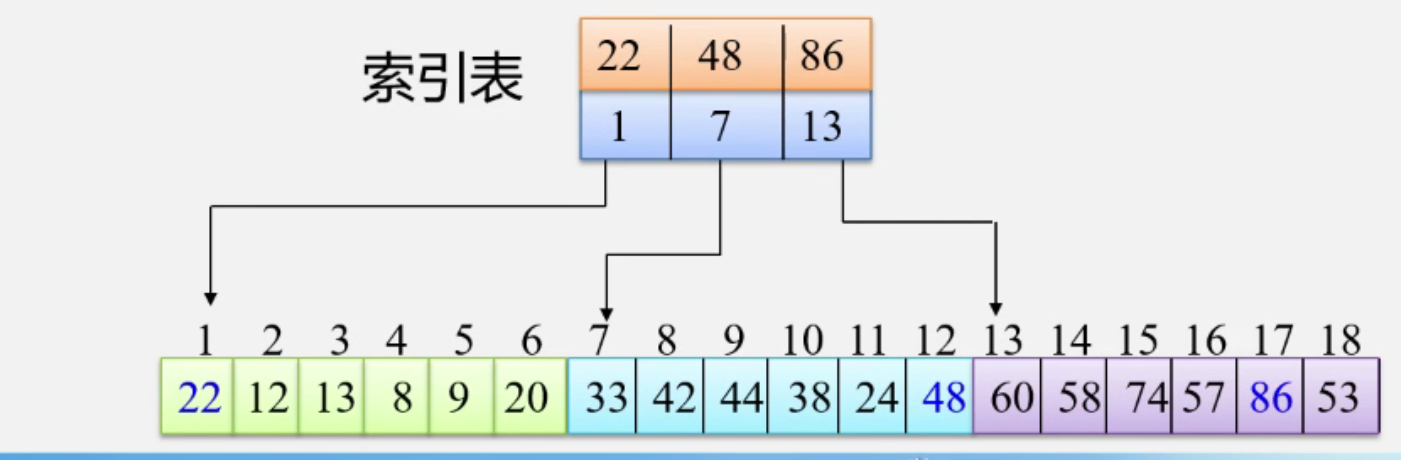 2. 建立索引表(存储结点的开始位置和块的最大值)
image.png

效率分析

  • 插入删除容易，不需要大量移动
  • 需要额外的索引空间
  • 既要快速查找，又经常动态变化，就可以采用分块查找。

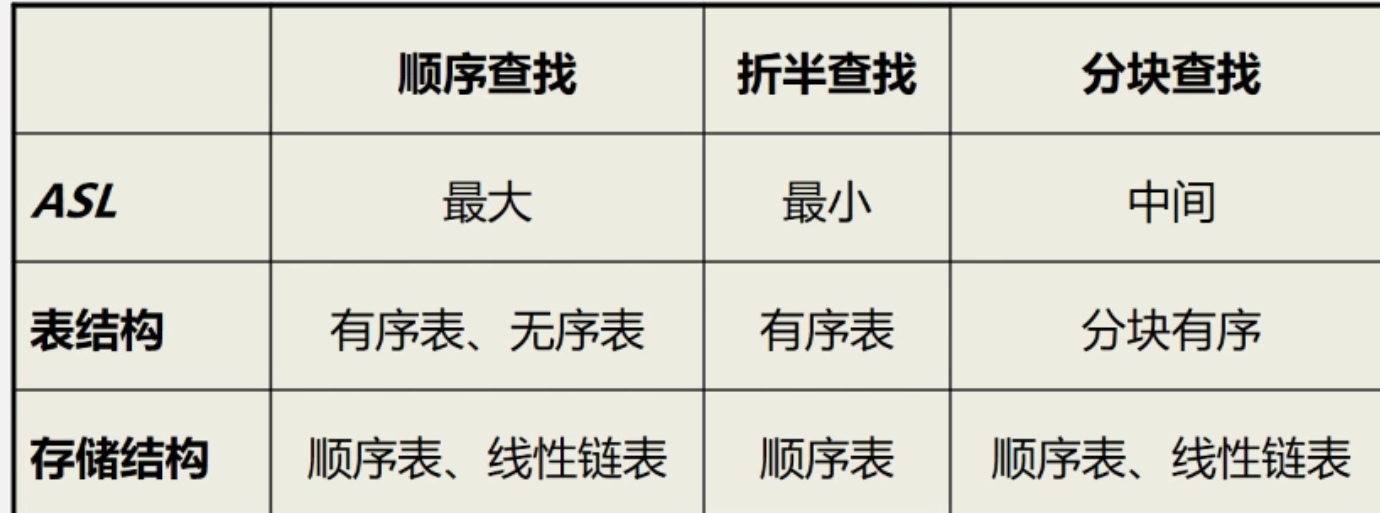
image.png

总结

image.png

三、树表的查找

当表在进行插入、删除操作频繁的时候，为了保证表的有序性，需要移动表当中的大量元素，这会导致效率的大幅度降低。这时候，我们就可以引入动态查找表: —-几种特殊性质的树
image.png

1. 二叉排序树

二叉树又称之为二叉搜索树，二叉查找树。

定义:

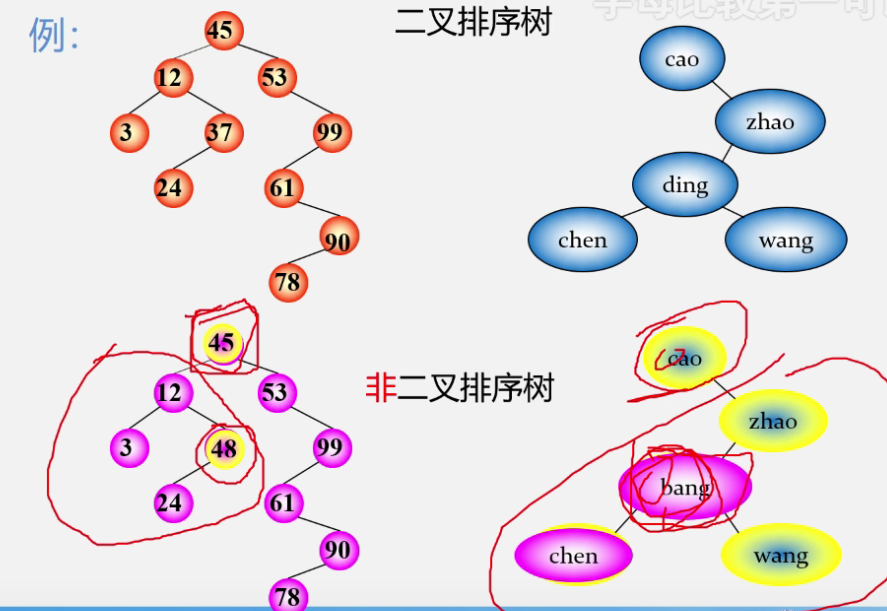
image.png
image.png

对于二叉排序树中序遍历，那么这个排序书就是递增的序列

查找算法

查找的原理

  • 查找关键字等于根结点，成功，返回结果
  • 否则
    • 若＜根结点，查左子树
    • 若＞根结点，查找右子树

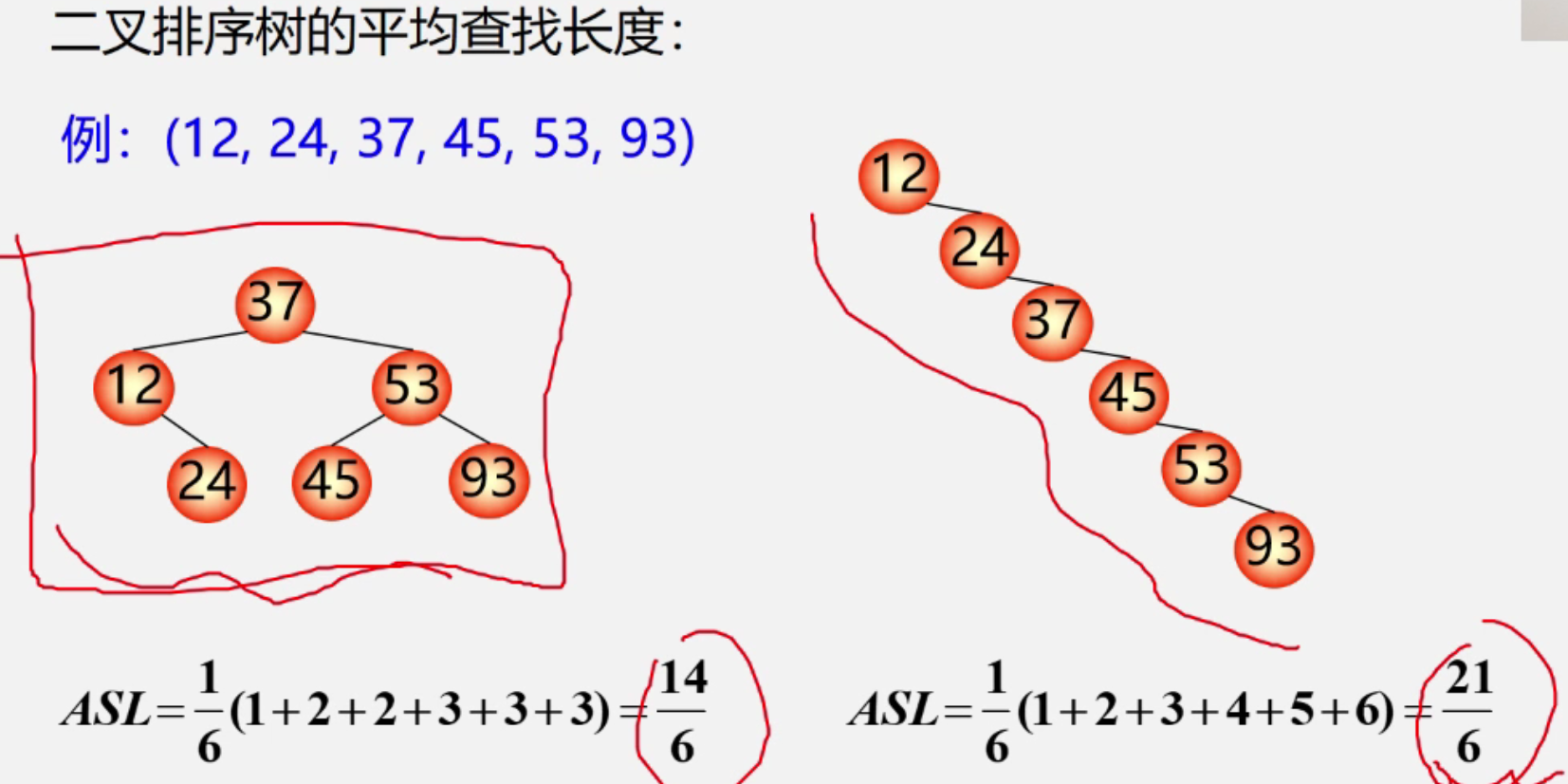
image.png

image.png

算法性能分析

image.png
对于一个含有n个结点的二叉排序树的平均查找长度与树的形态相关， 一个均衡的二叉树的平均查找长度相当于一个判定树，而一个不均衡的二叉树相当于在做顺序查找，时间复杂度竟然高达o(n)！
那么，怎么提高形态不均衡的二叉排序树的查找效率，平衡化处理(下一节的平衡二叉树)

插入和生成算法

  • 插入的元素一定是叶子结点

image.png

练习

image.png

删除结点

从二叉排序树当中删除一个结点，不能吧以该结点为根的子树全部删除，只能删除该借点，并且还需要保证删除后的二叉树还具有排序二叉树的性质。
中序遍历之后，还能得到一个递增有序的序列;
结点删除有三种情况

  1. 删除的结点是叶子结点
    1. 直接删除就可以了
  2. 当删除结点只有左或者右边子树，直接替换可以了

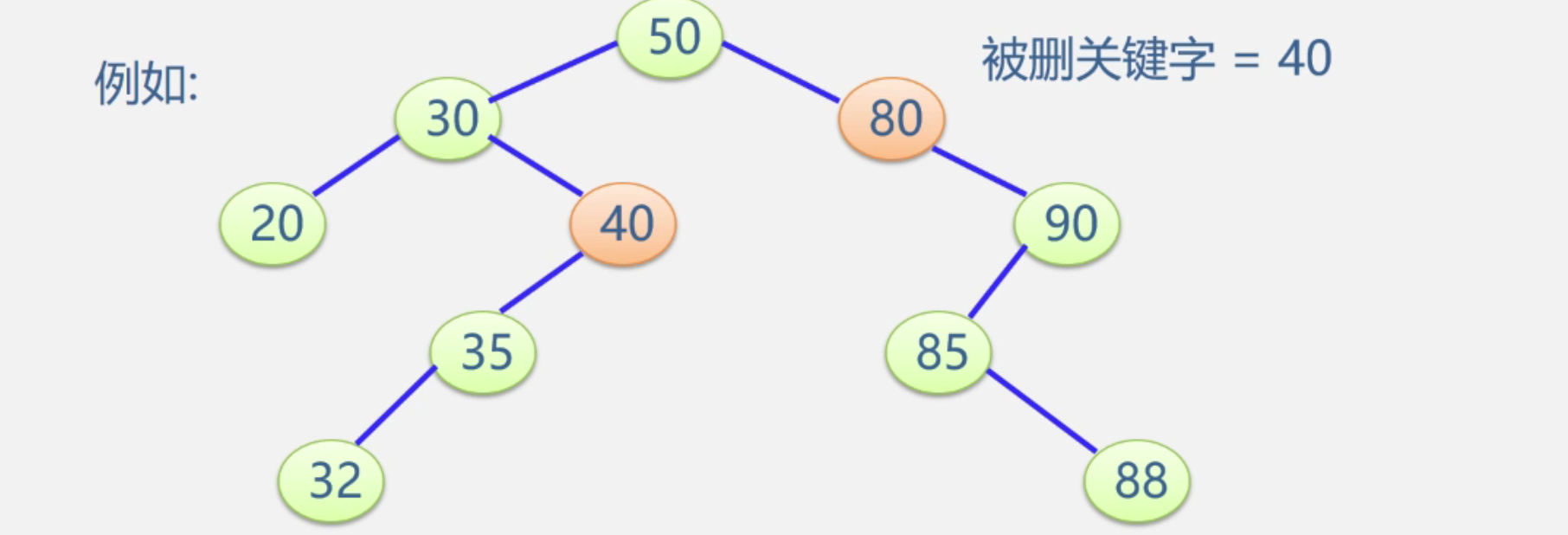
image.png

  1. 要删除的结点即有左子树，又有右子树。

    第一种方法
    左子树当中值最大的结点
    用中序遍历的前驱结点来替换
    第二种方法
    用中序遍历的后继结点来替换
    右子树的最小结点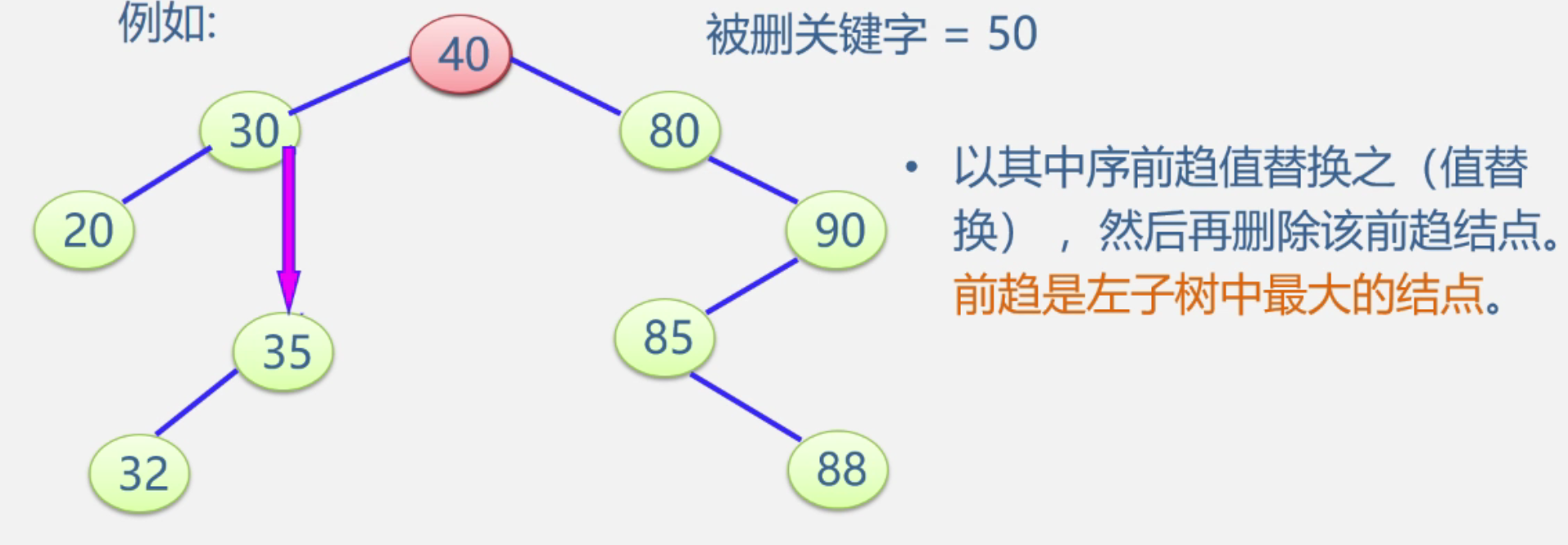
    image.png

2. 平衡二叉树

定义

  • 一颗平衡二叉树或者空树，具有下列性质的二叉排序树；
  • 左子树和右子树高度差的绝对值＜等于1

  • 左子树和右子树也是平衡二叉排序树

    为了计算方便，给每个结点增加一个数字，给出该结点左子树和右子树的高度差，这个数字就是平衡因子
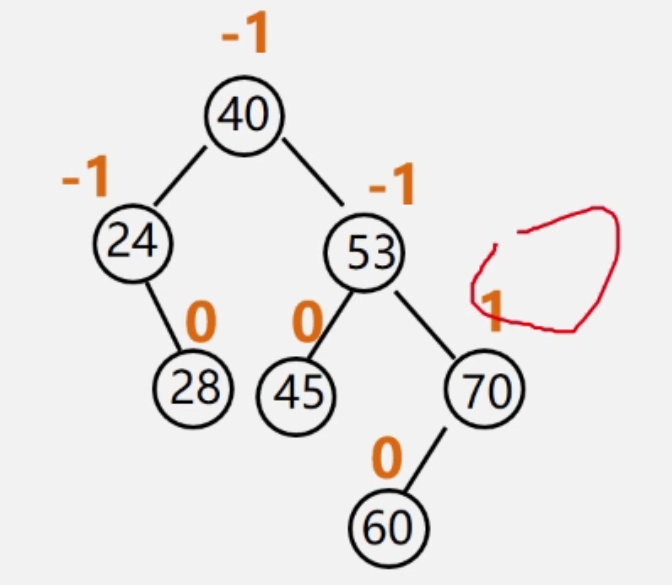
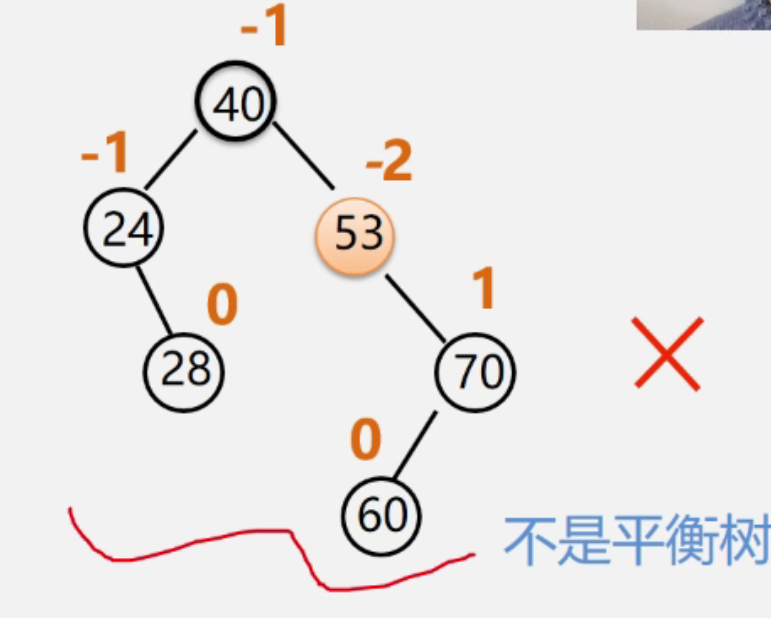
    image.png

image.png
image.png

平衡的调整方法

当我们在平衡二叉树当中插入一个新结点的时候，有可能会倒入失衡，就是出现平衡因子的绝对值大于1、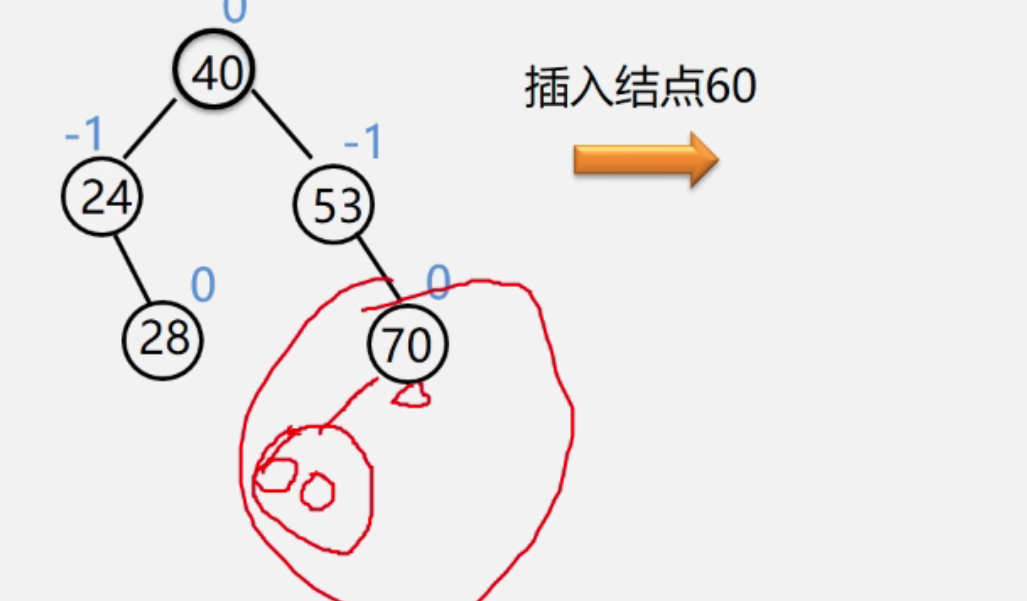
image.png

平衡调整的四种类型

小练习: 将下列失衡情况，做平衡调整

  1. 降低高度
  2. 保持二叉排序树的性质

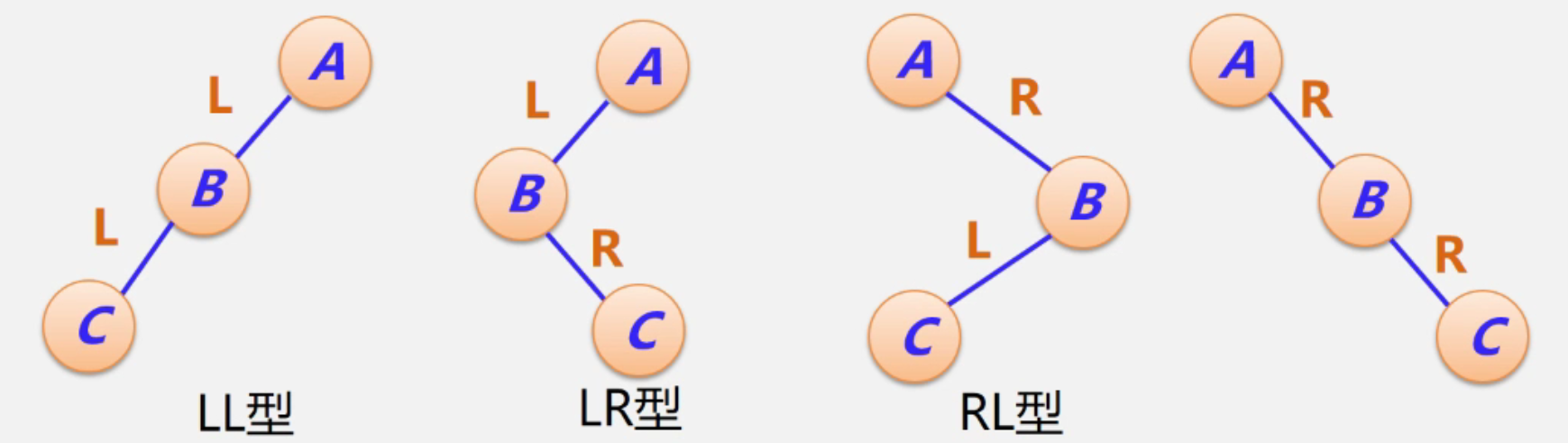
image.png

LL型

中间结点上升，若4有右结点,则作为5的左结点出现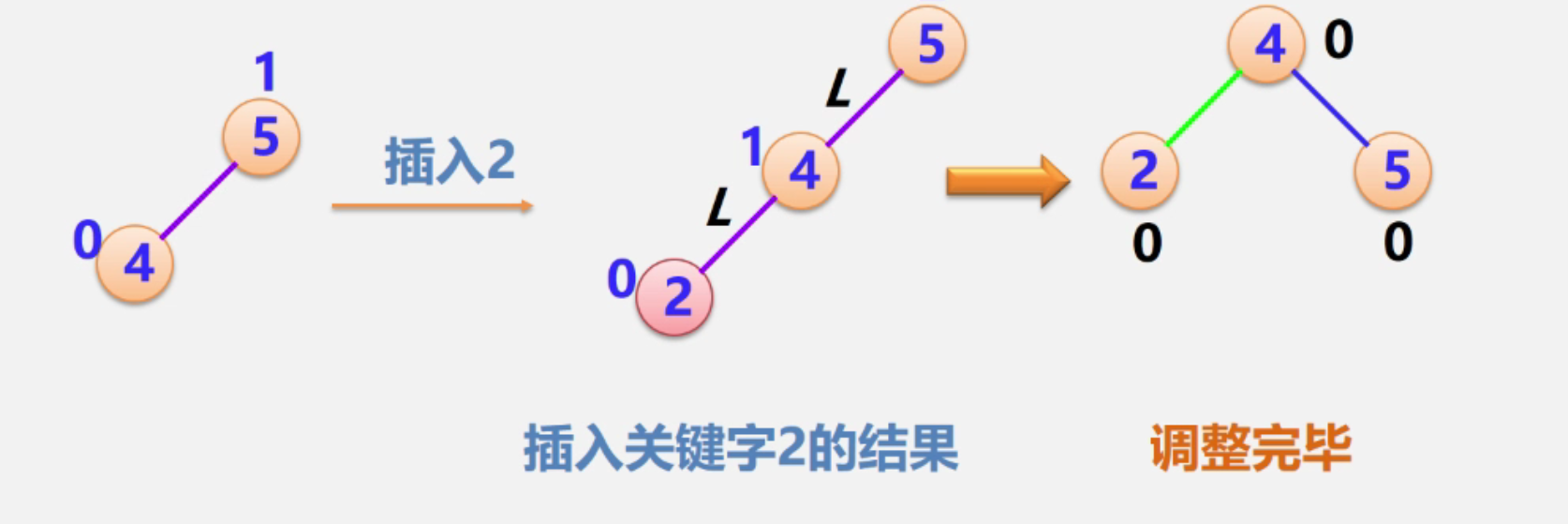
image.png

RR型

中间结点上升，原来根结点作为上升结点的左孩子，上升结点的左孩子则为原来根结点的右孩子。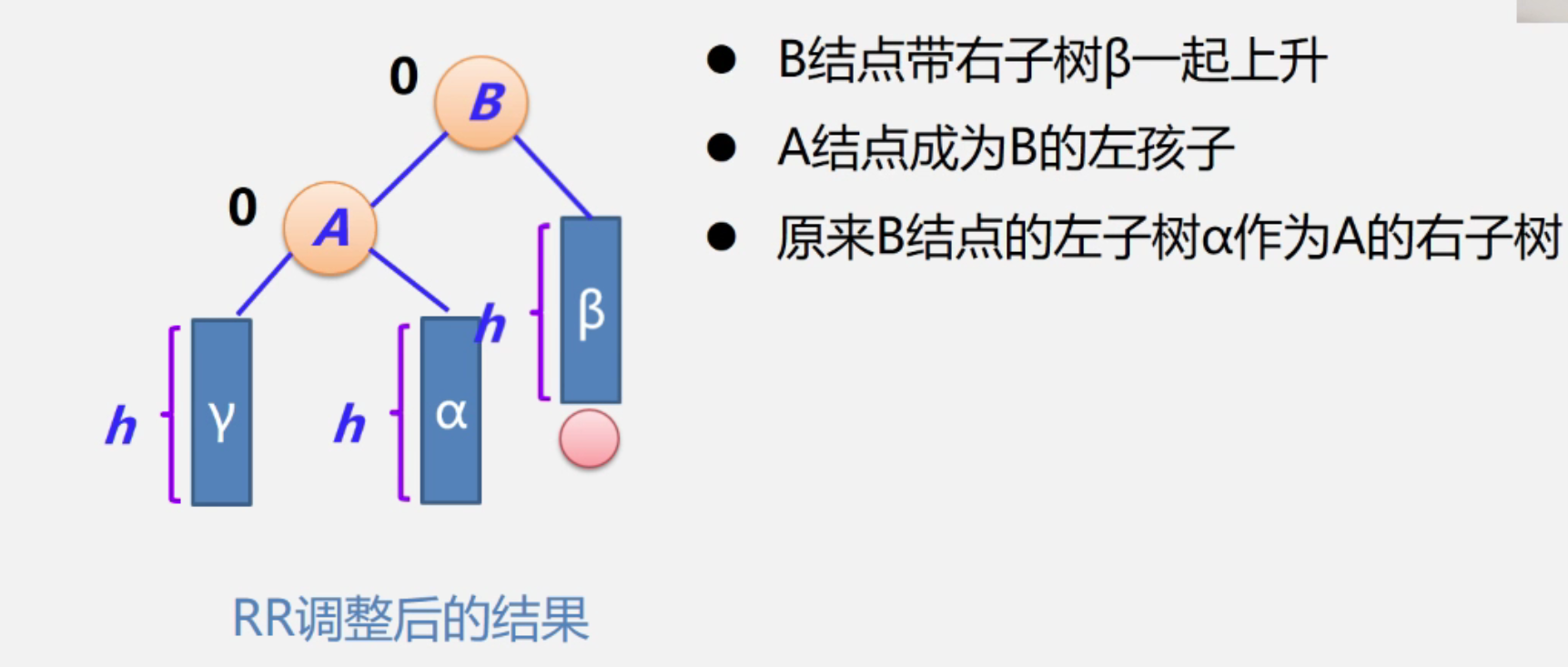
image.png

LR型

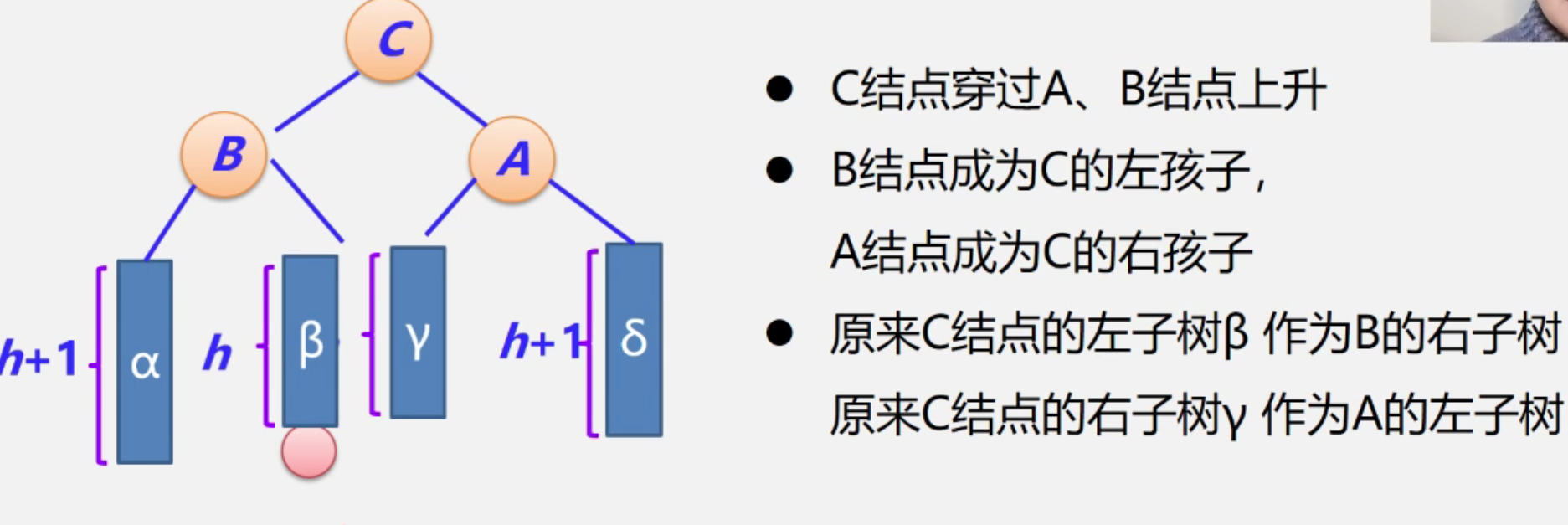
image.png

RL型

不管是什么类型，都采取，取中间值上升的想法，平衡调整过后的树，一定要是一个二叉排序树。

例题

image.png，将这个序列整成AVL树。

四、散列表

概念

记录存储位置与关键字的存在关系，对应的关系—hash函数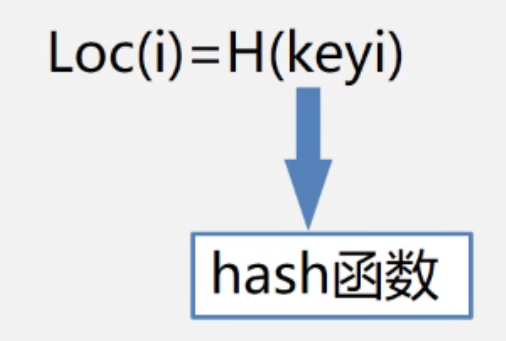
image.png
image.png

查找效率高，空间效率低

术语

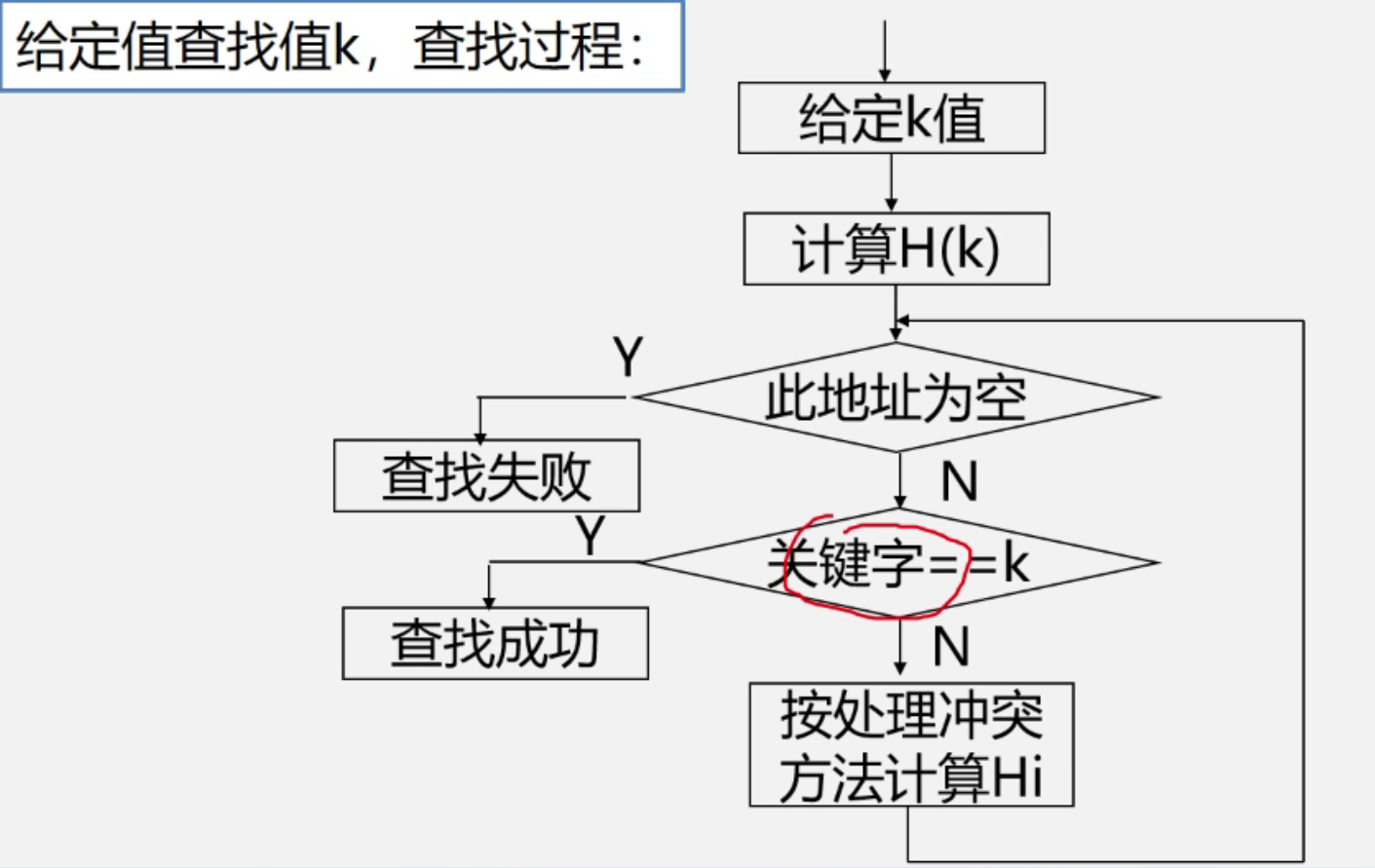
  • 散列方法（杂凑法）

    去某个函数，函数按照给出关键字计算元素的存储位置，查找的同时，由同一个函数对给定值K计算地址，将k与地址单元中元素关键对比，确定查找是否成功。

  • 散列函数

    散列方法当中所用到的转换函数。
    image.png

  • 冲突

    不同的关键码映射到了同一个散列地址
    image.png

  • 同义词

    具有相同函数值的多个关键字

散列表的构造

散列表的冲突是不可能避免的，只可能适当减少

使用散列表要解决的问题

  1. 构造好的散列函数
    1. 简单
    2. 减少空间的浪费
  2. 制定一个好的解决冲突的方案

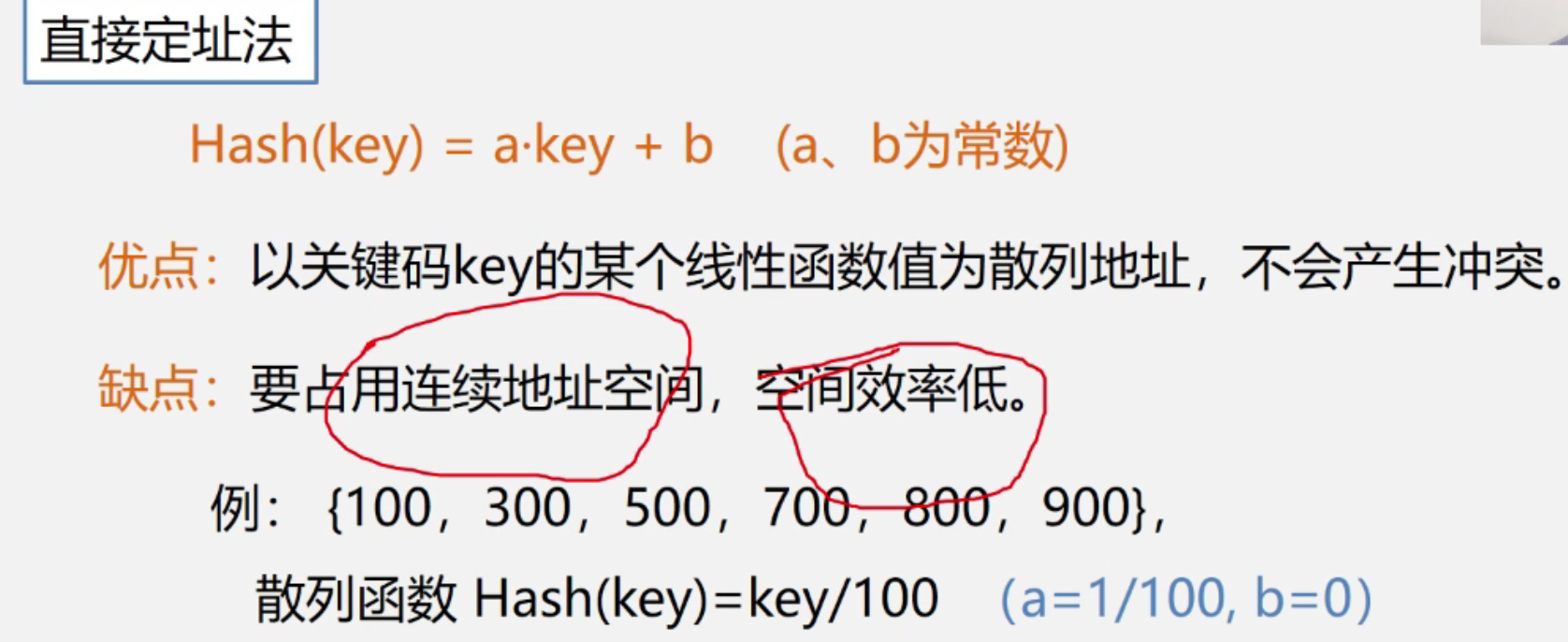
构造散列函数

构造散列函数需要考虑的因素

  1. 执行的速度
  2. 关键字长度
  3. 散列表的大小
  4. 关键字的分布
  5. 查找的频率

    直接定址法

    image.png

    除留余数法

    image.png

解决冲突的方法

image.png

开放地址法

有冲突的时候，就去寻找下一个空的散列地址，只要散列表足够大，空的散列地址总能够找到。
image.png

  • 例如

image.png,采用线性探针法，来解决冲突

链地址法

将相同散列地址的记录成链接成一个单链表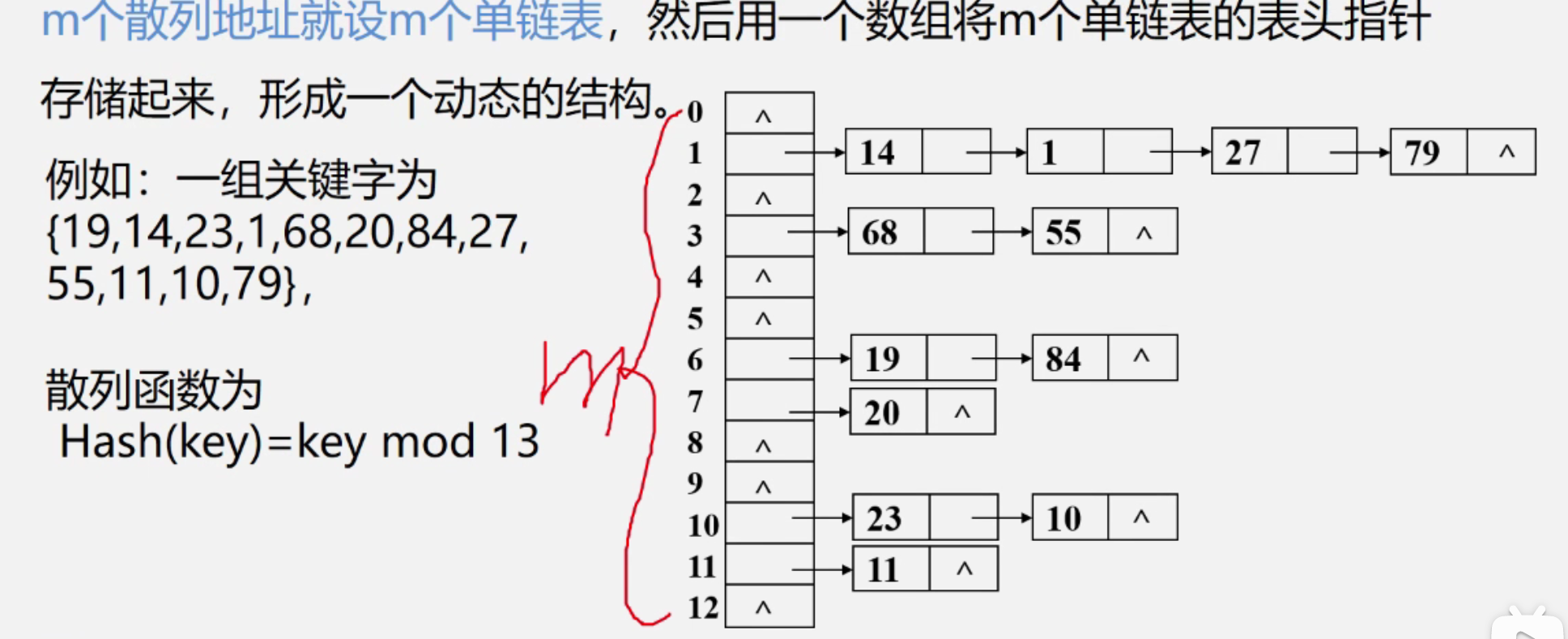
image.png

散列表的查找与性能分析

查找

image.pngimage.png