一、串

内容受到限制的线性表

1. 定义

串由0个或者多个任意字符组成的有限序列

  • n=0为空串

    1. s= “fdasfads”

    术语

  • 子串:

    • 一个串当中任意连续字符组成子序列
    • 真子串不包含自身
      1. "asdf";
      2. //子串
      3. “” “abc” "ab" "abcdf"...

  • 主串：

  • 字符位置:字符在序列中序号为该字符在串当中位置
  • 子串的位置: 子串第一个字符在主串当中的位置
  • 空格串: 由若干个空格组成字符

image.png
串相等，两个串长度相等，并且各个对应位置的字符都需要相同，这两个字符串才会相等。
所有的空串都是相等的

2. 串类型定义和存储结构运算

数据对象属于全字符
数据关系依然是线性表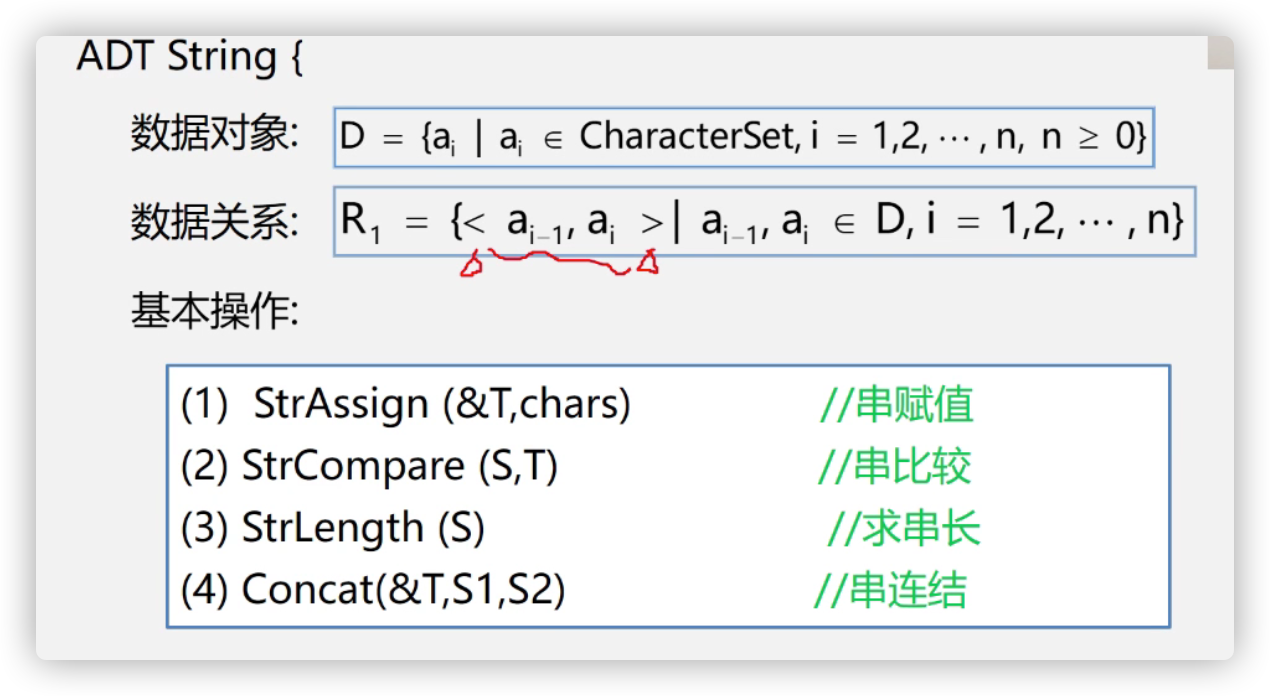
image.png
串的元素逻辑关系和线性表相同，串也可以采用线性表相同的存储结构

  • 串: 顺序串与链串

    顺序存储结构

    ```c

    define MAXSIZE 100

    typedef struct{ int length; //必须要字符创 char ch[MAXSIZE]; }SqStr;
  1. <a name="XH7UD"></a>
  2. ### 链式存储结构
  4. - **操作方便，但是存储密度较低**
  5.    - **串所占的存储/实际分配的存储**
  6. - 可以将多个字符存放在一个节点当中，以克服其缺点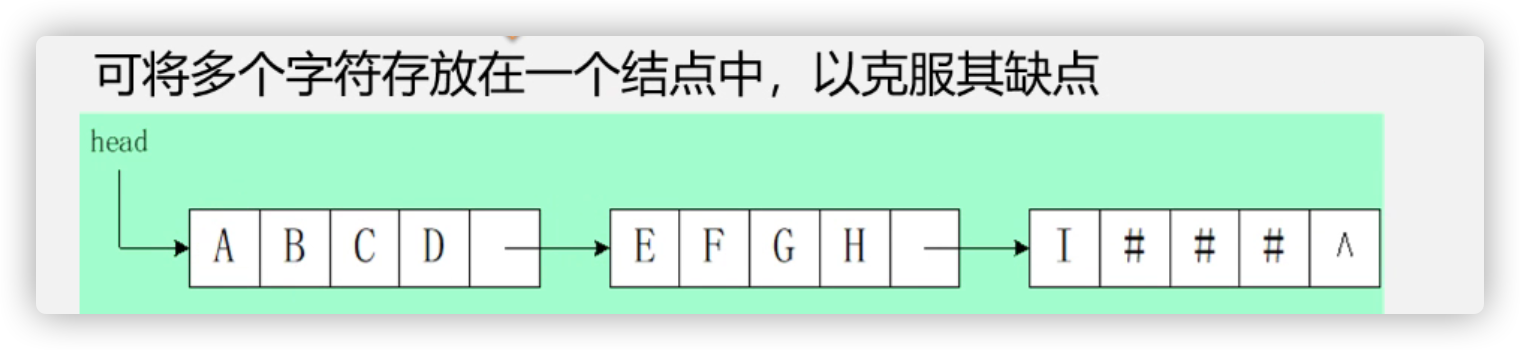
  8. ![image.png](https://cdn.nlark.com/yuque/0/2021/png/12423141/1638520408395-64fcb570-8740-4e0c-a8de-414201bcc033.png#clientId=ue5495cea-29ed-4&from=paste&height=163&id=u7ca4b18b&margin=%5Bobject%20Object%5D&name=image.png&originHeight=326&originWidth=1362&originalType=binary&ratio=1&size=108188&status=done&style=none&taskId=uffd21dde-b9c9-42f3-9d67-4094cc4f88c&width=681)<br />![image.png](https://cdn.nlark.com/yuque/0/2021/png/12423141/1638520720633-435661f7-f251-4cf1-9173-b023f33a3893.png#clientId=ue5495cea-29ed-4&from=paste&height=175&id=u257425f3&margin=%5Bobject%20Object%5D&name=image.png&originHeight=350&originWidth=1520&originalType=binary&ratio=1&size=144283&status=done&style=none&taskId=u4d38eb73-2c24-413d-ad95-4482a17319e&width=760)
  9. ```c
  10. //块链串
  11. #define CHUNKSIZE 80
  12. typedef struct Chunk{
  13.     char ch[CHUNKSIZE];
  14.     struct Chunk *next;
  15. }Chunk;
  17. typedef struct {
  18.     Chunk *head,*tali; //头尾
  19.     int curLen; //当前长度
  20. }LString;

实际当中顺序存储结构会用的更多

3. 串的模式匹配算法

  • 算法的目的

    1.    **确定主串与所含子串第一次出现的位置(定位)**

  • 算法种类

    • BE
    • KMP

      BF算法

      简单的暴力破解，匹配算法
      image.png
  1. int index_BF(SqStr S,SqStr T,int pos){
  2.     int i =pos; //从哪个开始查找
  3.     int j = 0;
  4.     while(i<=S.length && j<=T.length){
  5.         if(S.ch[i] == T.ch[j]){
  6.             //当前字符匹配成功
  7.             i++;j++;
  8.         }else{
  9.             //没有匹配成功回溯
  10.             i = i-j+2; 
  11.             j=1;
  12.         }
  13.     }
  14.     if(j>=T.length){
  15.         return i-T.length; 
  16.     }else{
  17.         return 0;
  18.     }
  20. }

KMP算法

二、数组

1. 定义

按一定格式排列起来的具有相同类型的元素集合

  • 一维数组，若线性表中数据元素为非结构的简单的元素，可以称为一维数组

  • 一维数组的逻辑结构: 线性结构 

    1. int num[5]={0,1,2,3,4};

  • 二维数组: 若干行，若干列

image.png

  1. typedef elemtype arr1[5][8]
  4. typedef elemtype2 arr2[2]
  5. typedef arr2 arr3[8] <#new#>

  • 三维数组

    • 若n-1维数组中元 线性结构是数据结构的特例

      数组结构又是线性表的扩展

  • 结构固定

    2. 抽象数据类型

  • 当 n = 2(二维数组)

  • b1:第一维(长度)的长度 b2:第二维(列数)的长度
  • aj1j2:
    • j1就是一维数组的下标(0<=j1<=b1-1)
    • j2就是二维数组的下标(0<=j2<=b1-1)

image.png

3. 顺序存储

  • 数组特点结构固定，维数和操作不会改变

  • 数组基本操作:初始化销毁取出修改，一般不会插入和删除

    一般使用顺序来存储！！

    例题: 每个元素占用四个字节，假设a[0]在2000单元，那么a[3] = a[0]+(4*3)

    （i)*L+a(第一个元素的单元地址)

两种存储方式

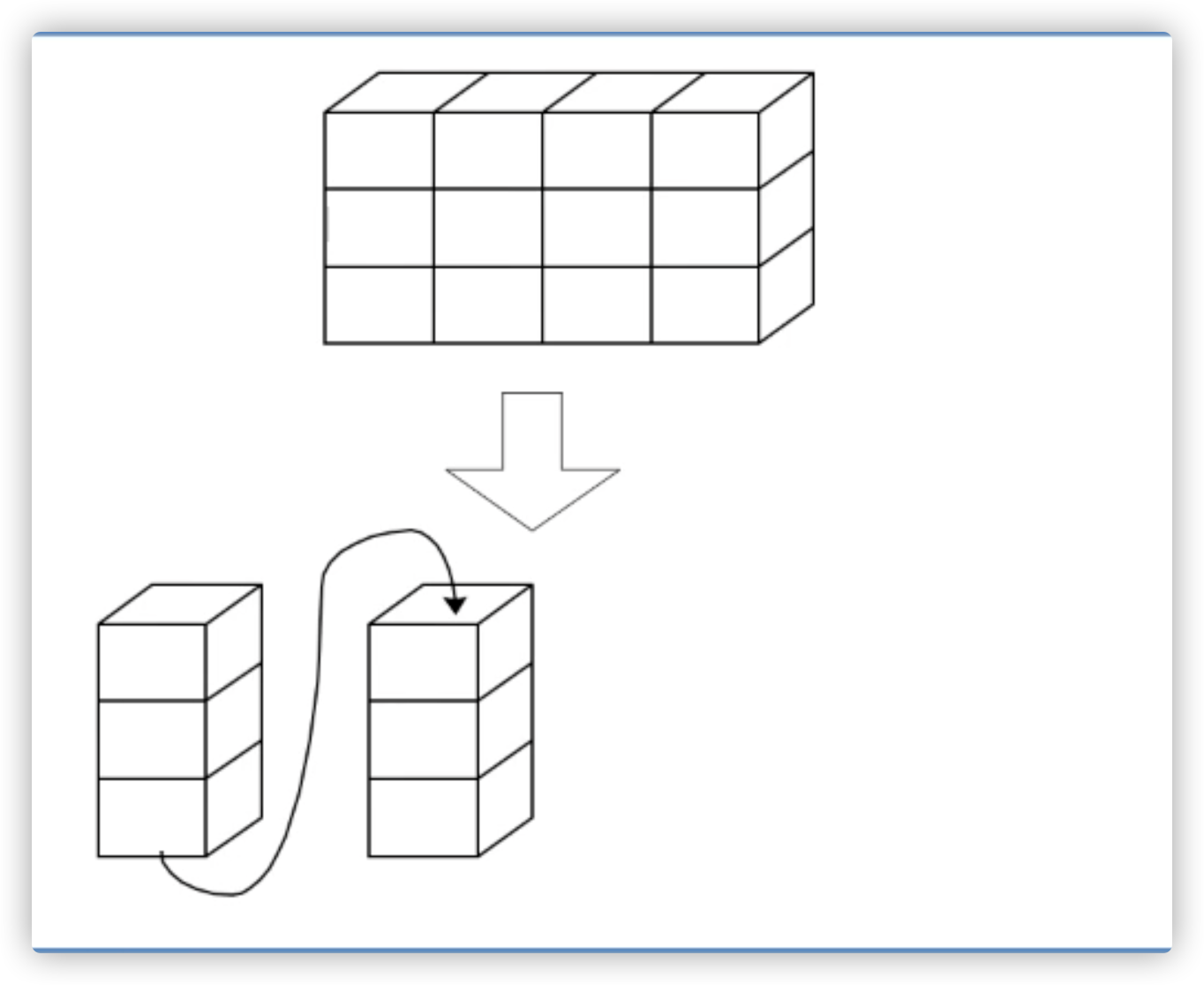
  • 行优先

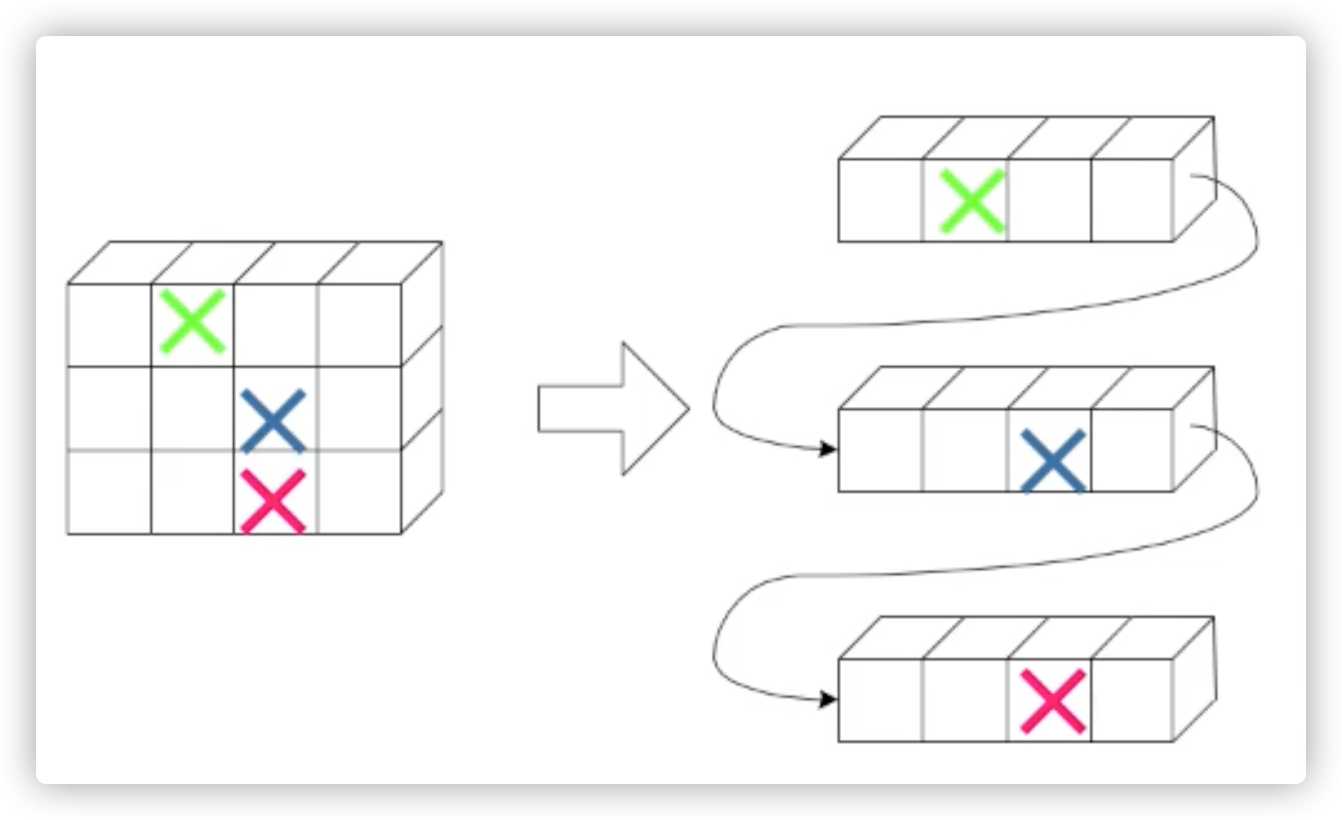
image.png

  • 列优先

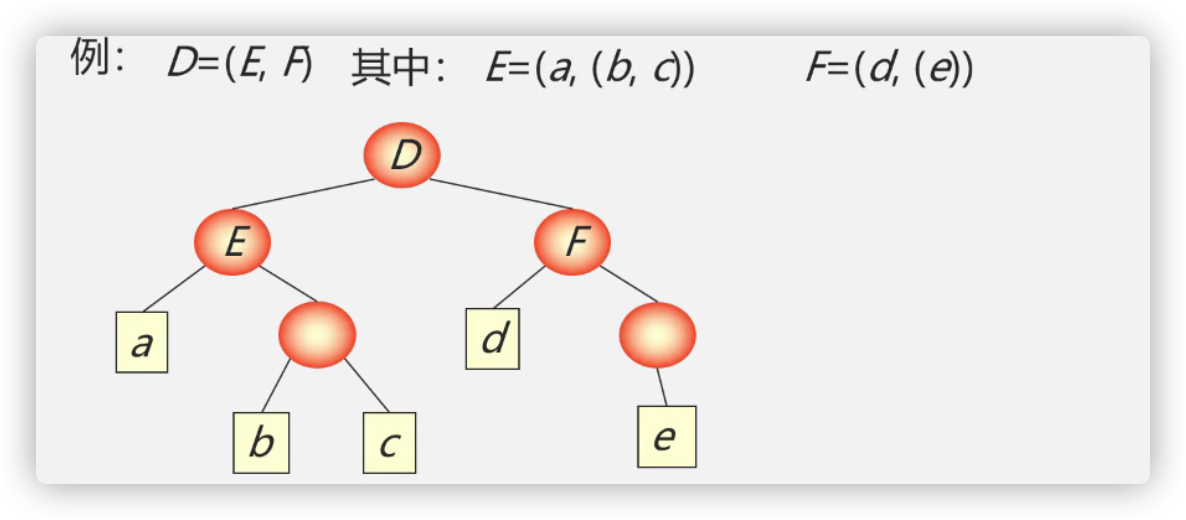
image.png

广义表

image.png

概述

LS = (a1,a2…an)

  • LS为表名，n为表的长度，每个a1为表的元素
  • 一般大写字母来表示广义表，小写字母表示原子

    表头

    如果LS不为空，第一个元素a1就是表头
    记作head(LS)=a1

    表头可以是原子，也可以是子表

表尾

除了表头之外其他元素组成的表
记作tail(LS)=(a2,….,an)

表尾不是最后的元素，而是一个子表



image.png

广义表的性质

  1. 广义表元素有次序，一个直接前驱和后继
  2. 广义表的长度定义为最外层所包含的元素个数
  3. 广义表的深度定义为广义表展开后所含括号的重数。
    1. 原子的深度为零
    2. ‘空表的深度’=1
  4. 广义表可以被其他的表共享
  5. 广义表也可以是递归表 ，深度无穷，长度有限
  6. 广义表是一种多层次的结构

image.png
广义表可以看成的线性表的推广，线性表是广义表的特例

广义表的常见运算

  1. 求表头GetHead()
    1. 表头可能是原子也可能是表
  2. 表尾GetTail()
    1. 表尾一定是一个表