4. 二叉树

前面介绍了数组、字典、字符串、链表、栈、队列的处理和应用方法。本节将会探讨平常相对很少用到、面试中却是老面孔的数据结构：二叉树。本节主要包括以下内容：

iOS 面试策略之算法基础4-5节 - 图1

  • 基本概念：实现，深度 ，二叉查找树
  • 二叉树的遍历
  • 苹果公司面试题：在 iOS 中展示二叉树

二叉树的基本概念

iOS 面试策略之算法基础4-5节 - 图2

首先介绍下二叉树。二叉树中每个节点最多有两个子节点，一般称为左子节点和右子节点，并且二叉树的子树有左右之分，其次序不能任意颠倒。下面是节点的 Swift 实现：

  1. public class TreeNode {
  2.   public var val: Int
  3.   public var left: TreeNode?
  4.   public var right: TreeNode?
  5.   public init(_val: Int) {
  6.     self.val = val
  7.   }
  8. }

一般在面试中，会给定二叉树的根节点。要访问任何其他节点，只要从起始节点开始往左/右走即可。

在二叉树中，节点的层次从根开始定义，根为第一层，树中节点的最大层次为树的深度。

  1. // 计算树的最大深度
  2. func maxDepth(root: TreeNode?) -> Int {
  3.   guard let root = root else {
  4.     return 0
  5.   }
  6.   return max(maxDepth(root.left), maxDepth(root.right)) + 1
  7. }

面试中，最常见的是二叉查找树，它是一种特殊的二叉树。它的特点就是左子树中节点的值都小于根节点的值，右子树中节点的值都大于根节点的值。那么问题来了，给你一棵二叉树，怎么判断它是二叉查找树？我们根据定义，可以写出以下解法：

  1. // 判断一颗二叉树是否为二叉查找树
  2. func isValidBST(root: TreeNode?) -> Bool {
  3.   return _helper(root, nil, nil)
  4. }
  6. private func _helper(node: TreeNode?, _ min: Int?, _ max: Int?) -> Bool {
  7.   guard let node = node else {
  8.     return true
  9.   }
  10.   // 所有右子节点都必须大于根节点
  11.   if let min = min, node.val <= min {
  12.     return false
  13.   }
  14.   // 所有左子节点都必须小于根节点
  15.   if let max = max, node.val >= max {
  16.     return false
  17.   }
  19.   return _helper(node.left, min, node.val) && _helper(node.right, node.val, max)
  20. }

上面的代码有这几个点值得注意：

  1. 二叉树本身是由递归定义的，所以原理上所有二叉树的题目都可以用递归来解
  2. 二叉树这类题目很容易就会牵涉到往左往右走，所以写 helper 函数要想到有两个相对应的参数
  3. 记得处理节点为 nil 的情况，尤其要注意根节点为 nil 的情况

二叉树的遍历

最常见的树的遍历有 3 种，前序、中序、后序遍历。这 3 种写法相似，无非是递归的顺序略有不同。面试时候有可能考察的是用非递归的方法写这 3 种遍历：用栈实现。

  1. // 用栈实现的前序遍历
  2. func preorderTraversal(root: TreeNode?) -> [Int] {
  3.   var res = [Int]()
  4.   var stack = [TreeNode]()
  5.   var node = root
  7.   while !stack.isEmpty || node != nil {
  8.     if node != nil {
  9.       res.append(node!.val)
  10.       stack.append(node!)
  11.       node = node!.left
  12.     } else {
  13.       node = stack.removeLast().right
  14.     }
  15.   }
  17.   return res
  18. }

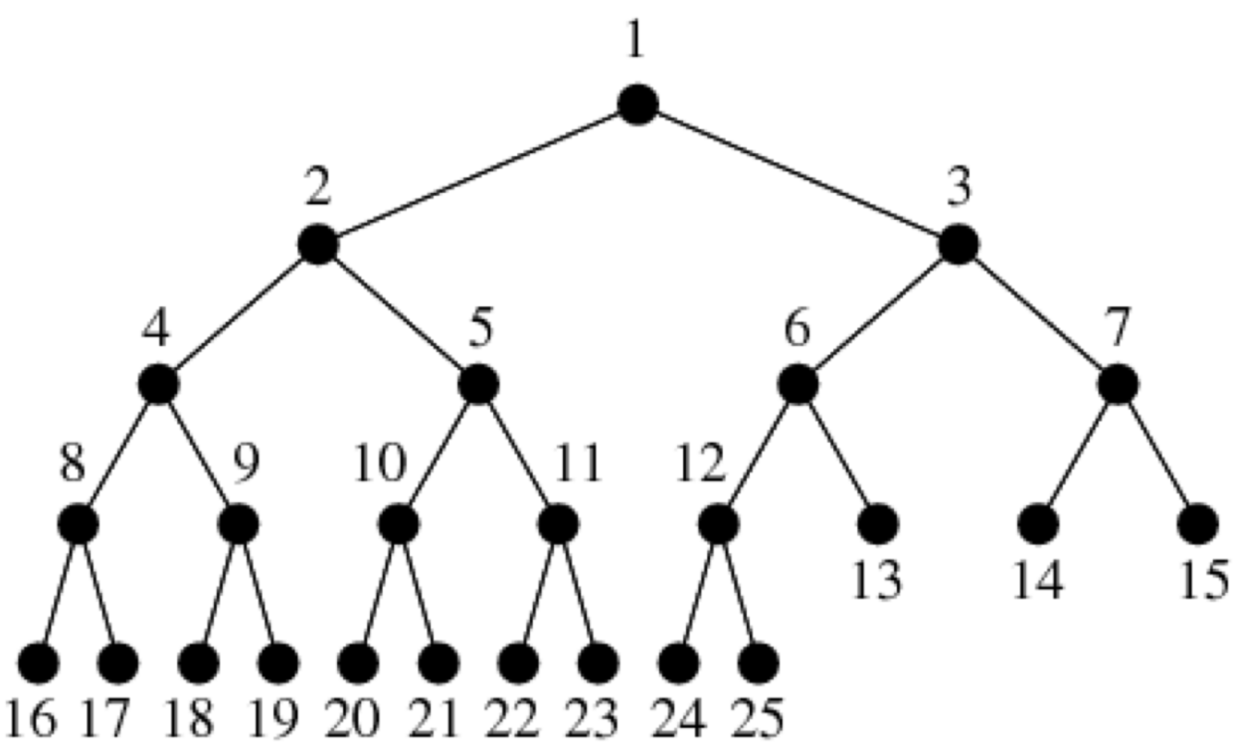
除了这三种最常见的遍历之外，还有一种遍历是层级遍历（广度优先遍历），请看下图：

iOS 面试策略之算法基础4-5节 - 图3

这棵树的层级遍历结果为[[1], [2, 3], [4, 5, 6, 7], [8, 9, 10, 11, 12, 13, 14, 15]]。

层级遍历相比于以上 3 种常见遍历的好处在于：如果构建一棵树，那么至少要知道中序遍历和前序/后序遍历中的一种，也就是至少要知道两种遍历方式；但是层级遍历自己便可以唯一确定一棵树。我们来看下面一道苹果公司的面试题。

二叉树面试实战题

请设计一个应用可以展示一颗二叉树。

首先一个简单的 App 是 MVC 架构，所以我们就要想，在 View 的层面上表示一棵二叉树？我们脑海中浮现树的结构是这样的：

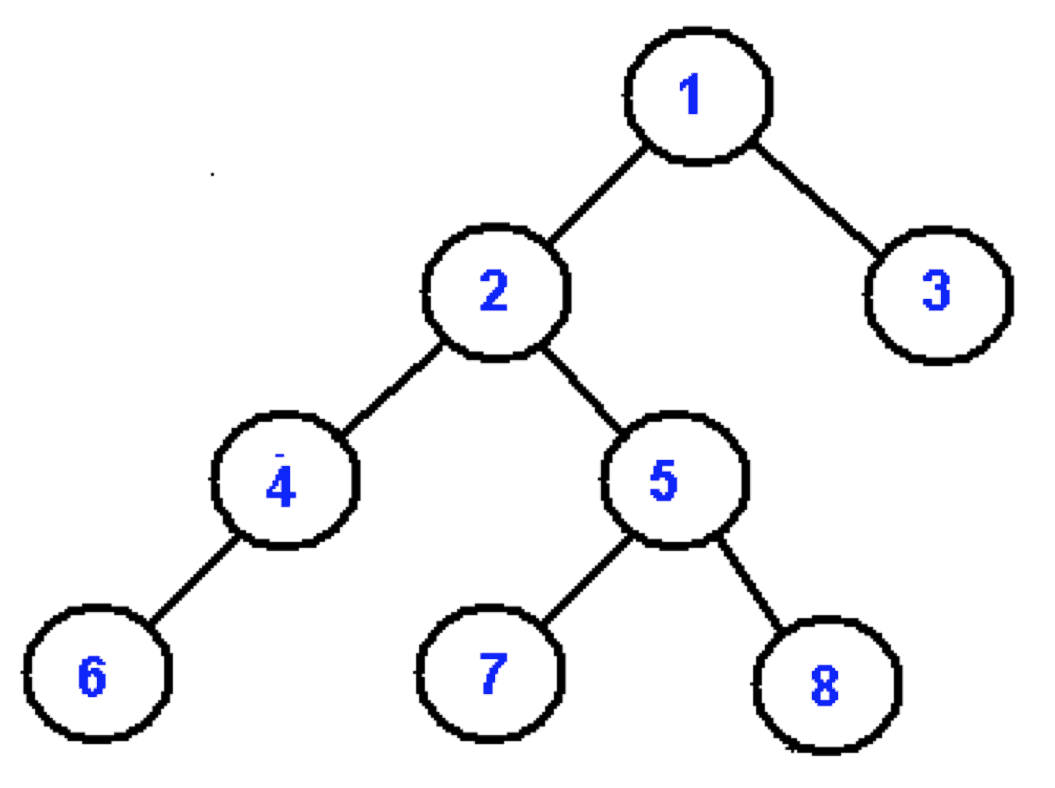
iOS 面试策略之算法基础4-5节 - 图4

所以是不是在 View 的界面上，每个节点弄个 UILabel 来表示，然后用数学方法计算每个 UIlabel 对应的位置，从而完美的显示上图的样子？

这个想法比较简单粗暴，是最容易想到，实现之后又是最直观展示一棵二叉树的，但是它有以下两个问题：

  • 每个 UILabel 的位置计算起来比较麻烦；
  • 如果一棵树有很多节点（比如1000个），那么当前界面就会显示不下了，这时候咋办？就算用 UIScrollView 来处理，整个树也会变得非常不直观，每个节点所对应的 UILabel 位置计算起来就会更费力。

要处理大量数据，我们就想到了 UITableView。假如每一个 cell 对应一个节点，以及其左、右节点，那么我们就可以清晰的展示一棵树。比如上图这棵树，用 UITableView 就可以写成这样：

iOS 面试策略之算法基础4-5节 - 图5

其中”#”表示空节点。明眼人可以看出，我们是按照层级遍历的方式布局整个 UITableView。这种做法解决了上面两个问题：

  • 无需进行位置计算，UITableView 提供复用 Cell，效率大幅提高
  • 面对很多节点的问题，可以先处理一部分数据，然后用处理 infinite scroll 的方式来加载剩余数据

接着问题来了，给你一棵二叉树，如何得到它的层级遍历？其实层级遍历就是图的广度优先遍历，而广度优先遍历很自然就会用到队列，所以我们不妨用队列来帮助实现树的层级遍历：

  1. func levelOrder(root: TreeNode?) -> [[Int]] {
  2.   var res = [[Int]]()
  3.   // 用数组来实现队列
  4.   var queue = [TreeNode]()
  6.   if let root = root {
  7.     queue.append(root)
  8.   }
  10.   while queue.count > 0 {
  11.     var size = queue.count
  12.     var level = [Int]()
  14.     for _ in 0 ..< size {
  15.       let node = queue.removeFirst()
  17.       level.append(node.val)
  18.       if let left = node.left {
  19.         queue.append(left)
  20.       }
  21.       if let right = node.right {
  22.         queue.append(right)
  23.       }
  24.     }
  25.     res.append(level)
  26.   }
  28.   return res
  29. }

总结

到这里为止，我们已经把重要的数据结构都分析了一遍。要知道，这些数据结构都不是单独存在的，我们在解决二叉树的问题时，用到了队列；解决数组的问题，也会用到字典或是栈。在真正面试或是日常开发中，最低的时间复杂度是首要考虑，接着是优化空间复杂度，其次千万不要忘记考虑边界情况。在Swift 中，用 let 和 var 的地方要区分清楚，该不该定义数据为 optional，有没有处理 nil 的情况都是很容易忽略的。

5. 排序和搜索

前几节中，我们主要探讨了数据结构：比如数组、链表、队列、树。这些数据结构都是了解 Swift 和算法的基础。从今以后的文章，我们将更多的关注于通用算法，这次我们就来聊聊排序和搜索。
排序的基本概念

说到排序，我们平常用的算法一般就以下几种：

名称 时间复杂度 空间复杂度 是否稳定
冒泡排序 O(n^2) O(1) 是
插入排序 O(n^2) O(1) 是
选择排序 O(n^2) O(1) 否
堆排序 O(nlogn) O(1) 否
归并排序 O(nlogn) O(n) 是
快速排序 O(nlogn) O(logn) 否
桶排序 O(n) O(k) 是

这些算法具体的定义本文不再赘述。一般情况下，好的排序算法性能是 O(nlogn)，坏的性能是 O(n^2)。本文在此用 Swift 示范实现归并排序和快速排序：

  1. // 归并排序
  2. func mergeSort(_ array: [Int]) -> [Int] {
  3.   guard array.count > 1 else {
  4.     return array
  5.   }
  7.   // 分割
  8.   let middleIndex = array.count / 2
  9.   let leftArray = mergeSort(Array(array[0..<middleIndex]))
  10.   let rightArray = mergeSort(Array(array[middleIndex..<array.count]))
  12.   // 归并
  13.   return merge(leftArray, rightArray)
  14. }
  16. // 合并两个已经按序排列的数组
  17. func merge(_ left: [Int], _ right: [Int]) -> [Int] {
  18.   var leftIndex = 0, rightIndex = 0
  19.   var orderedArray = [Int]()
  21.   while leftIndex < left.count || rightIndex < right.count {
  22.     if leftIndex < left.count && rightIndex < right.count {
  23.       if left[leftIndex] <= right[rightIndex] {
  24.         orderedArray.append(left[leftIndex])
  25.         leftIndex += 1
  26.       } else {
  27.         orderedArray.append(right[rightIndex])
  28.         rightIndex += 1
  29.       }
  30.     } else if leftIndex < left.count {
  31.       orderedArray.append(left[leftIndex])
  32.       leftIndex += 1
  33.     } else {
  34.       orderedArray.append(right[rightIndex])
  35.       rightIndex += 1
  37.     }
  38.   }
  40.   return orderedArray
  41. }
  43. // 快速排序
  44. func quicksort(_ array:[Int]) -> [Int] {
  45.   guard array.count > 1 else {
  46.     return array
  47.   }
  48.   let pivot = array[array.count / 2]
  49.   let left = array.filter { $0 < pivot }
  50.   let middle = array.filter { $0 == pivot }
  51.   let right = array.filter { $0 > pivot }
  53.   return quicksort(left) + middle + quicksort(right)
  54. }

表格中有一个特例是桶排序，它是将输入的数组分配到一定数量的空桶中，每个空桶再单独排序。当输入的数组是均匀分配时，桶排序的时间复杂度为 O(n)。举个微软的面试题来当例子：

有三种颜色（红，黄，蓝）的球若干，要求将所有红色的球放在黄色球的前面，最后放上所有的蓝色球。

这道题目最直接的解法就是桶排序。首先第一次遍历，统计有多少个红色球（假设 x 个），多少个黄色球（假设 y 个），和多少个蓝色球（假设 z 个）。然后再一次遍历，数组前部 x 个位置填充红色球，中间 y 个位置放上对应数量的黄色球，最后 z 个位置再放上蓝色球。

另外解释一下稳定的意思：相等的键值，如果排过序后与原来未排序的次序相同，则称此排序算法为稳定。举个例子：

  1. // 原数组
  2. [[2, 1], [1,3], [1,4]]
  4. // 排序算法一
  5. [[1,3], [1,4], [2, 1]]
  6. // 排序算法二
  7. [[1,4], [1,3], [2, 1]]

我们注意到排序算法一和二的区别就在于对[1, 3], [1, 4]这两个元素的处理。排序算法一中，这两个元素位置与原数组相同，故称其为稳定算法。而排序算法二则是不稳定算法。
在 Swift 中，排序的使用如下：

  1. // 以升序排列为例，原数组可改变
  2. array.sort()
  4. // 以降序排列为例，原数组不可改变
  5. newArray = array.sorted(by: >)
  7. // 字典键值排序示例
  8. let keys = Array(map.keys)
  9. let sortedKeys = keys.sorted() {
  10.   return map[$0]! > map[$1]!
  11. }

在 Java 中，其自带的 sort 函数部分是用归并排序实现的。而在 Swift 源代码中，sort 函数采用的是一种内省算法（IntroSort）。它由堆排序、插入排序、快速排序 3 种算法构成，依据输入的深度选择最佳的算法来完成。本书关注的重点是实战，所以不做展开。对源代码感兴趣的读者可以在 GitHub 上读取苹果公司的 Swift 开源库。

搜索的基本概念

一般最直接的搜索就是遍历集合，然后找到满足条件的元素。这种直接的暴力搜索法实现起来简单，但是当输入数据十分巨大的时候，搜索起来就会很慢（复杂度 O(n)）。本节将探讨算法复杂度更低、效果更好的搜索方法 —— 二分搜索。

二分搜索，即在有序数组中，查找某一特定元素的搜索。它从中间的元素开始，如果中间的元素是要找的元素，则返回；若中间元素小于要找的元素，则要找的元素一定在大于中间元素的那一部分，那只需搜索那部分即可；反之搜索小于中间元素的部分即可。重复以上步骤，直到找到或确认该元素不存在为止。这样每一次搜索，就能减小一办的搜索范围，所以它的算法复杂度为 O(logn)。

Swift 实现二分搜索

  1. // 假设nums是一个升序数组
  2. func binarySearch(_ nums: [Int], _ target: Int) -> Bool {
  3.   var left = 0, mid = 0, right = nums.count - 1
  5.   while left <= right {
  6.     mid = (right - left) / 2 + left
  8.     if nums[mid] == target {
  9.       return true
  10.     } else if nums[mid] < target {
  11.       left = mid + 1
  12.     } else {
  13.       right = mid - 1
  14.     }
  15.   }
  17.   return false
  18. }

这里要注意两个细节：

第一，mid 定义在 while 循环外面，如果定义在里面，则每次循环都要重新给 mid 分配内存空间，造成不必要的浪费；定义在循环之外，每次循环只是重新赋值；
第二，每次重新给 mid 赋值不能写成 mid = (right + left) / 2。这种写法表面上看没有问题，但当数组的长度非常大、算法又已经搜索到了最右边部分的时候，那么 right + left 就会非常之大，造成溢出导致程序崩溃。所以解决问题的办法是写成 mid = (right - left) / 2 + left。

当然，我们可以用递归来实现二分搜索：

  1. func binarySearch(nums: [Int], target: Int) -> Bool {
  2.   return binarySearch(nums: nums, target: target, left: 0, right: nums.count - 1)
  3. }
  5. func binarySearch(nums: [Int], target: Int, left: Int, right: Int) -> Bool {
  6.   guard left <= right else {
  7.     return false
  8.   }
  10.   let mid = (right - left) / 2 + left
  12.   if nums[mid] == target {
  13.     return true
  14.   } else if nums[mid] < target {
  15.     return binarySearch(nums: nums, target: target, left: mid + 1, right: right)
  16.   } else {
  17.     return binarySearch(nums: nums, target: target, left: left, right: mid - 1)
  18.   }
  19. }

排序实战

直接来看一道 Facebook, Google, Linkedin 都考过的面试题。

已知有很多会议，如果有这些会议时间有重叠，则将它们合并。 比如有一个会议的时间为 3 点到 5 点，另一个会议时间为 4 点到 6 点，那么合并之后的会议时间为 3 点到6点

解决算法题目第一步永远是把具体问题抽象化。这里每一个会议我们已知开始时间和结束时间，就可以写一个类来定义它：

  1. public class MeetingTime {
  2.   public var start: Int
  3.   public var end: Int
  4.   public init(_ start: Int, _ end: Int) {
  5.     self.start = start
  6.     self.end = end
  7.   }
  8. }

然后题目说已知有很多会议，就是说我们已知有一个 MeetingTime 的数组、所以题目就转化为写一个函数，输入为一个 MeetingTime 的数组，输出为一个将原数组中所有重叠时间都处理过的新数组。

  1. func merge(meetingTimes: [MeetingTime]) -> [MeetingTime] {}

下面来分析一下题目怎么解。最基本的思路是遍历一次数组，然后归并所有重叠时间。举个例子：[[1, 3], [5, 6], [4, 7], [2, 3]]。这里我们可以发现[1, 3]和[2, 3]可以归并为[1, 3]，[5, 6]和[4, 7]可以归并为[4, 7]。所以这里就提出一个要求：要将所有可能重叠的时间尽量放在一起，这样遍历的时候可以就可以从前往后一个接着一个的归并。于是很自然的想到 — 按照会议开始的时间排序。

这里我们要对一个 class 进行排序，而且要自定义排序方法，在 Swift 中可以这样写：

  1. meetingTimes.sortInPlace() {
  2.   if $0.start != $1.start {
  3.     return $0.start < $1.start
  4.   } else {
  5.     return $0.end < $1.end
  6.   }
  7. }

意思就是首先对开始时间进行升序排列，如果它们相同，就比较结束时间。

有了排好顺序的数组，要得到新的归并后的结果数组，我们只需要在遍历的时候，每次比较原数组（排序后）当前会议时间与结果数组中当前的会议时间，假如它们有重叠，则归并；如果没有，则直接添加进结果数组之中。所有代码如下：

  1. func merge(meetingTimes: [MeetingTime]) -> [MeetingTime] {
  2.   // 处理特殊情况
  3.   guard meetingTimes.count > 1 else {
  4.     return meetingTimes
  5.   }
  7.   // 排序  
  8.   var meetingTimes = meetingTimes.sort() {
  9.     if $0.start != $1.start {
  10.       return $0.start < $1.start
  11.     } else {
  12.       return $0.end < $1.end
  13.     }
  14.   }
  16.   // 新建结果数组
  17.   var res = [MeetingTime]()
  18.   res.append(meetingTimes[0])
  20.   // 遍历排序后的原数组，并与结果数组归并    
  21.   for i in 1..<meetingTimes.count {
  22.     let last = res[res.count - 1]
  23.     let current = meetingTimes[i]
  24.     if current.start > last.end {
  25.       res.append(current)
  26.     } else {
  27.       last.end = max(last.end, current.end)
  28.     }
  29.   }
  31.   return res
  32. }

搜索实战

第一题：版本崩溃

一般的二分搜索基本上稍微有点基本功的都能写出来。所以，真正面试的时候，最多也就是问问概念。真正的搜索相关面试题，长下面这个样子：

有一个产品发布了 n 个版本。它遵循以下规律：假如某个版本崩溃了，后面的所有版本都会崩溃。 举个例子：一个产品假如有 5 个版本，1，2，3 版都是好的，但是第 4 版崩溃了，那么第 5 个版本（最新版本）一定也崩溃。第 4 版则被称为第一个崩溃的版本。 现在已知一个产品有 n 个版本，而且有一个检测算法 func isBadVersion(version: Int) -> Bool 可以判断一个版本是否崩溃。假设这个产品的最新版本崩溃了，求第一个崩溃的版本。

分析这种题目，同样还是先抽象化。我们可以认为所有版本为一个数组 [1, 2, 3, …, n]，现在我们就是要在这个数组中检测出满足isBadVersion(version) == true中version 的最小值。

很容易就想到二分搜索，假如中间的版本是好的，第一个崩溃的版本就在右边，否则就在左边。我们来看一下如何实现：

  1. func findFirstBadVersion(version: n) -> Int {
  2.   // 处理特殊情况
  3.   guard n >= 1 else {
  4.     return -1
  5.   }
  7.   var left = 1, right = n, mid = 0
  9.   while left < right {
  10.     mid = (right - left) / 2 + left
  11.     if isBadVersion(mid) {
  12.       right = mid
  13.     } else {
  14.       left = mid + 1
  15.     }
  16.   }
  18.   return left    // return right 同样正确
  19. }

这个实现方法要注意两点

  1. 1.当发现中间版本(mid)是崩溃版本的时候，只能说明第一个崩溃的版本小于等于中间版本。所以只能写成 right = mid；
  2. 2.当检测到剩下一个版本的时候，我们已经无需在检测直接返回即可，因为它肯定是崩溃的版本。所以 while 循环不用写成 left <= right。

第二题：搜索旋转有序数组

上面的题目是一个简单的二分搜索变种。我们来看一个复杂版本的：

一个有序数组可能在某个位置被旋转。给定一个目标值，查找并返回这个元素在数组中的位置，如果不存在，返回 -1。假设数组中没有重复值。 举个例子：[0, 1, 2, 4, 5, 6, 7]在4这个数字位置上被旋转后变为[4, 5, 6, 7, 0, 1, 2]。搜索 4 返回 0 。搜索 8 则返回 -1 。

假如这个有序数组没有被旋转，那很简单，我们直接采用二分搜索就可以解决。现在被旋转了，还可以采用二分搜索吗？

我们先来想一下旋转之后的情况。第一种情况是旋转点选的特别前，这样旋转之后左半部分就是有序的；第二种情况是旋转点选的特别后，这样旋转之后右半部分就是有序的。如下图：

iOS 面试策略之算法基础4-5节 - 图6

那么怎么判断是结果 1 还是结果 2 呢？我们可以选取整个数组中间元素(mid) ，与数组的第1个元素(left)进行比较 — 如果 mid > left，则是旋转结果1，那么数组的左半部分就是有序数组，我们可以在左半部分进行正常的二分搜索；反之则是结果二，数组的右半部分为有序数组，我们可以在右半部分进行二分搜索。

这里要注意一点，即使我们一开始清楚了旋转结果，也要判断一下目标值所落的区间。对于旋转结果1，数组左边最大的值是mid，最小值是left。假如要找的值target落在这个区间内，则使用二分搜索。否则就要在右边的范围内搜索，这个时候相当于回到了一开始的状态，有一个旋转的有序数组，只不过我们已经剔除了一半的搜索范围。对于旋转结果2，也类似处理。全部代码如下：

  1. func search(nums: [Int], target: Int) -> Int {
  2.   var (left, mid, right) = (0, 0, nums.count - 1)
  4.   while left <= right {
  5.     mid = (right - left) / 2 + left
  7.     if nums[mid] == target {
  8.       return mid
  9.     }
  11.     if nums[mid] >= nums[left] {
  12.       if nums[mid] > target && target >= nums[left] {
  13.         right = mid - 1
  14.       } else {
  15.         left = mid + 1
  16.       }
  17.     } else {
  18.       if nums[mid] < target && target <= nums[right] {
  19.         left = mid + 1
  20.       } else {
  21.         right = mid - 1
  22.       }
  23.     }
  24.   }
  26.   return -1
  27. }

大家可以想一下假如旋转后的数组中有重复值比如[3,4,5,3,3,3]该怎么处理？

iOS中搜索与排序的配合使用

iOS 面试策略之算法基础4-5节 - 图7

上图是iOS中开发的一个经典案例：新闻聚合阅读器(RSS Reader)。因为新闻内容经常会更新，所以每次下拉刷新这个UITableView或是点击右上角刷新按钮，经常会有新的内容加入到原来的dataSource中。刷新后合理插入新闻，就要运用到搜索和排列。

笔者在这里提供一个方法。首先，写一个 ArrayExtensions.swift；

  1. extension Array {
  2.   func indexForInsertingObject(object: AnyObject, compare: ((a: AnyObject, b: AnyObject) -> Int)) -> Int {
  3.     var left = 0
  4.     var right = self.count
  5.     var mid = 0
  7.     while left < right {
  8.       mid = (right - left) / 2 + left
  10.       if compare(a: self[mid] as! AnyObject, b: object) < 0 {
  11.         left = mid + 1
  12.       } else {
  13.         right = mid
  14.       }
  15.     }
  17.     return left
  18.   }
  19. }

然后在 FeedsViewController (就是显示所有新闻的 tableView 的 controller )里面使用这个方法。一般情况下，FeedsViewController 里面会有一个 dataSource，比如一个装新闻的 array。这个时候，我们调用这个方法，并且让它每次都按照新闻的时间进行排序：

  1. let insertIdx = news.indexForInsertingObject(object: singleNews) { (a, b) -> Int in
  2.   let newsA = a as! News
  3.   let newsB = b as! News
  4.   return newsA.compareDate(newsB)
  5. }
  7. news.insert(singleNews, at: insertIdx)

这里你需要在 News 这个 model 里实现 compareDate 这个函数。

总结

排序和搜索在 Swift 中的应用场景很多，比如 tableView 中对于 dataSource 的处理。二分搜索是一种十分巧妙和高效的搜索方法，它会经常配合排序出现在各种日常开发中。当然，二分搜索也会出现各种各样的变种，其实万变不离其宗，关键是想方法每次减小一半的搜索范围即可。

小编推荐阅读