6. 深度优先和广度优先

之前介绍了最简单的搜索法：二分搜索。虽然它的算法复杂度非常低只有 O(logn)，但使用起来也有局限：只有在输入是排序的情况下才能使用。这次讲解两个更复杂的搜索算法:

iOS 面试策略之算法基础6-7节 - 图1

  • 深度优先搜索（Depth-First-Search，以下简称DFS）
  • 广度优先搜索（Breadth-First-Search，以下简称BFS）

基本概念

DFS 和 BFS 的具体定义这里不做赘述。笔者谈谈自己对此的形象理解：假如你在家中发现钥匙不见了，为了找到钥匙，你有两种选择：

  1. 从当前角落开始，顺着一个方向不停的找。假如这个方向全部搜索完毕依然没有找到钥匙，就回到起始角落，从另一个方向寻找，直到找到钥匙或所有方向都搜索完毕为止。这种方法就是 DFS。
  2. 从当前角落开始，每次把最近所有方向的角落全部搜索一遍，直到找到钥匙或所有方向都搜索完毕为止。这种方法就是 BFS。

我们假设共有 10 个角落，起始角落为 1，它的周围有 4 个方向，如下图：

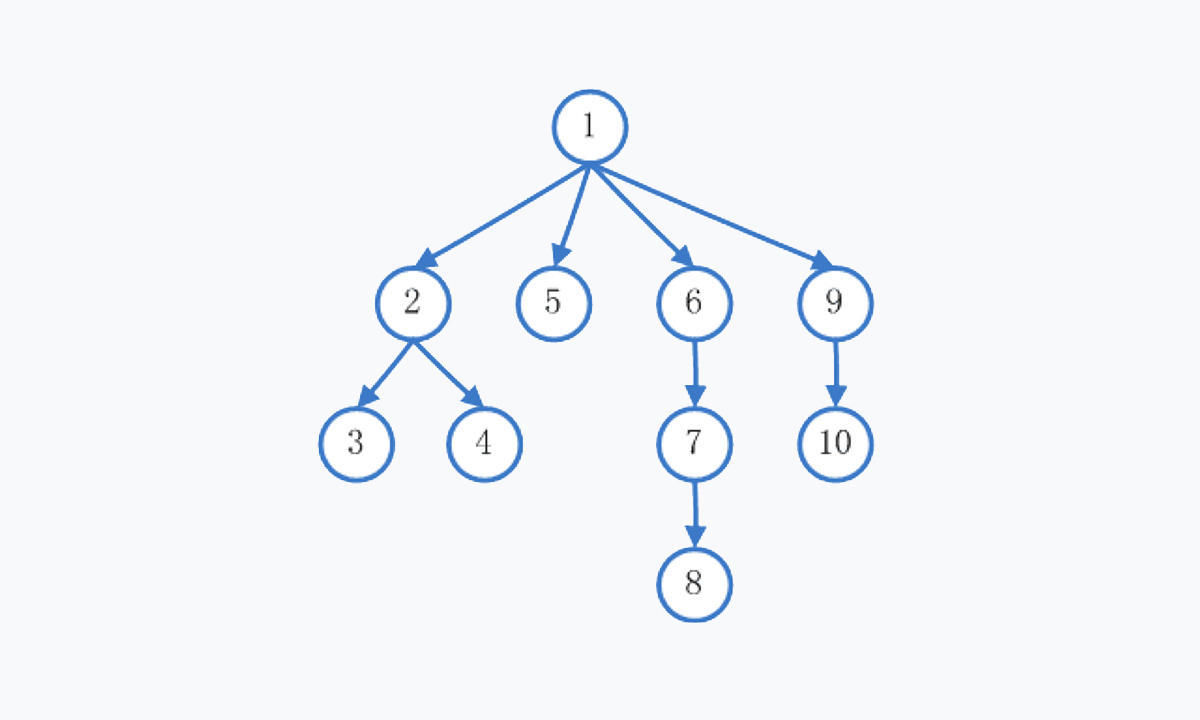
iOS 面试策略之算法基础6-7节 - 图2

DFS 的搜索步骤为：

  • 1
  • 2 -> 3 -> 4
  • 5
  • 6 ->7 -> 8
  • 9 -> 10

即每次把一个方向彻底搜索完全后，才返回搜索下一个方向。

BFS 的搜索步骤为：

  • 1
  • 2 -> 5 -> 6 -> 9
  • 3 -> 4
  • 7
  • 10
  • 8

即每次访问上一步周围所有方向上的角落。

细心的朋友会记得，我之前在讲二叉树的时候，讲到了前序遍历和层级遍历，而这两者本质上就是 DFS 和 BFS。

DFS 的 Swift 实现：

  1. func dfs(_ root: Node?) {
  2.     guard let root = root else {
  3.         return
  4.     }
  6.     visit(root)
  7.     root.visited = true
  9.     for node in root.neighbors {
  10.         if !node.visited {
  11.             dfs(node)
  12.         }
  13.     }
  15. }

BFS 的 Swift 实现：

  1. func bfs(_ root: Node?) {
  2.     var queue = [Node]()
  4.     if let root = root {
  5.         queue.append(root)
  6.     }
  8.     while !queue.isEmpty {
  9.         let current = queue.removeFirst()
  11.         visit(current)
  12.         current.visited = true
  14.         for node in current.neighbors {
  15.             if !node.visited {
  16.                 queue.append(node)
  17.             }
  18.         }
  19.     }
  20. }

永远记住：DFS 的实现用递归，BFS 的实现用循环（配合队列）。

iOS 实战演练

硅谷面试 iOS 工程师，有这样一个环节，给你 1 ~ 1.5 小时，从头开始实现一个小 App。我们来看这样一个题目：

实现一个找单词 App : 给定一个初始的字母矩阵，你可以从任一字母开始，上下左右，任意方向、任意长度，选出其中所有单词。

iOS 面试策略之算法基础6-7节 - 图3

很多人拿到这道题目就懵了，完全不是我们熟悉的 UITableView 或者 UICollectionView 啊，这要咋整。我们来一步步分析。

第一步：实现字母矩阵

首先，我们肯定有个字符二阶矩阵作为输入，姑且记做：matrix: [[Character]]。现在要把它展现在手机上，那么可行的方法，就是创建一个 UILabel 二维矩阵，记做 labels: [[UILabel]]，矩阵中每一个 UILabel 对应的内容就是相应的字母。同时，我们可以维护 2 个全局变量，xOffset 和 yOffset。然后在for循环中创建相应的 UILabel 同时将其添加进 lables 中便于以后使用，代码如下：

  1. var xOffset = 0
  2. var yOffset = 0
  3. let cellWidth = UIScreen.mainScreen().bounds.size.width / matrix[0].count
  4. let cellHeight = UIScreen.mainScreen().bounds.size.height / matrix.count
  6. for i in 0 ..< matrix.count {
  7.   for j in 0 ..< matrix[0].count {
  8.     let label = UILabel(frame: CGRect(x: xOffset, y: yOffset, width: cellWidth, height: cellHeight))
  9.     label.text = String(matrix[i][j])
  10.     view.addSubView(label)
  11.     labels[i][j] = label
  12.     xOffset += cellWidth
  13.   }
  14.   xOffset = 0
  15.   yOffset += cellHeight
  16. }

第二步：用 DFS 实现搜索单词

现在要实现搜索单词的核心算法了。我们先简化要求，假如只在字母矩阵中搜索单词 “crowd” 该怎么做？
首先我们要找到 “c” 这个字母所在的位置，然后再上下左右找第二个字母 “r” ，接着再找字母 “o” ······ 以此类推，直到找到最后一个字母 “d” 。如果没有找到相应的字母，我们就回头去首字母 “c” 所在的另一个位置，重新搜索。

这里要注意一个细节，就是我们不能回头搜索字母。比如我们已经从 “c” 开始向上走搜索到了 “r” ，这个时候就不能从 “r” 向下回头 — 因为 “c” 已经访问过了。所以这里需要一个 var visited: [[Bool]] 来记录访问记录。代码如下：

  1. func searchWord(_ board: [[Character]]) -> Bool {
  2.     guard board.count > 0 && board[0].count > 0 else {
  3.         return false
  4.     }
  6.     let (m, n) = (board.count, board[0].count)
  7.     var visited = Array(repeating: Array(repeating: false, count: n), count: m)
  9.     for i in 0 ..< m {
  10.         for j in 0 ..< n {
  11.             if board[i][j] == "c" && dfs(board, Array("crowd"), m, n, i, j, &visited, 0) {
  12.                 return true
  13.             }
  14.         }
  15.     }
  17.     return false
  18. }
  20. func dfs(_ board: [[Character]], _ wordContent: [Character], _ m: Int, _ n: Int, _ i: Int, _ j: Int, _ visited: inout [[Bool]], _ index: Int) -> Bool {
  21.     if index == wordContent.count {
  22.         return true
  23.     }
  25.     guard i >= 0 && i < m && j >= 0 && j < n else {
  26.         return false
  27.     }
  28.     guard !visited[i][j] && board[i][j] == wordContent[index] else {
  29.         return false
  30.     }
  32.     visited[i][j] = true
  34.     if dfs(board, wordContent, m, n, i + 1, j, &visited, index + 1) || dfs(board, wordContent, m, n, i - 1, j, &visited, index + 1) || dfs(board, wordContent, m, n, i, j + 1, &visited, index + 1) || dfs(board, wordContent, m, n, i, j - 1, &visited, index + 1) {
  35.         return true
  36.     }
  38.     visited[i][j] = false
  39.     return false
  40. }

第三步：优化算法，进阶

好了现在我们已经知道了怎么搜索一个单词了，那么多个单词怎么搜索？首先题目是要求找出所有的单词，那么肯定事先有个字典，根据这个字典，我们可以知道所选字母是不是可以构成一个单词。所以题目就变成了：

已知一个字母构成的二维矩阵，并给定一个字典。选出二维矩阵中所有横向或者纵向的单词。
也就是实现以下函数：

  1. func findWords(_ board: [[Character]], _ dict: Set<String>) -> [String] {}

我们刚才已经知道如何在矩阵中搜索一个单词了。所以最暴力的做法，就是在矩阵中，搜索所有字典中的单词，如果存在就添加在输出中。

这个做法显然复杂度极高：首先，每次 DFS 的复杂度就是 O(n2 )。字母矩阵越大，搜索时间就越长；其次，字典可能会非常大，如果每个单词都搜索一遍，开销太大。这种做法的总复杂度为 O(m· n2)，其中m为字典中单词的数量，n 为矩阵的边长。

这时就要引入 Trie 树(前缀树) 。前缀树是一种有序树，用于保存关联数组，特别适用于保存字符串。就这道题目而言，首先我们把字典转化为前缀树，这样的好处在于它可以检测矩阵中字母构成的前缀是不是一个单词的前缀，如果不是就没必要继续 DFS 下去了。这样我们就把搜索字典中的每一个单词，转化为了只搜字母矩阵。代码如下：

  1. func findWords(_ board: [[Character]], _ dict: Set<String>) -> [String] {
  2.   var res = [String]()
  4.   let (m, n) = (board.count, board[0].count)
  6.   let trie = _convertSetToTrie(dict)
  7.   var visited = Array(repeating: Array(repeating: false, count: n), count: m)
  9.   for i in 0 ..< m {
  10.     for j in 0 ..< n {
  11.       _dfs(board, m, n, i, j, &visited, &res, trie, "")
  12.     }
  13.   }
  15.   return res
  16. }
  18. private func _dfs(_ board: [[Character]], _ m: Int, _ n: Int, _ i: Int, _ j: Int, inout _ visited: [[Bool]], inout _ res: [String], _ trie: Trie, _ str: String) {
  19.   // 越界
  20.   guard i >= 0 && i < m && j >= 0 && j < n else {
  21.     return
  22.   }
  24.   // 已经访问过了
  25.   guard !visited[i][j] else {
  26.     return
  27.   }
  29.   // 搜索目前字母组合是否是单词前缀
  30.   var str = str + "\(board[i][j])"
  31.   guard trie.prefixWith(str) else {
  32.     return
  33.   }
  35.   // 确认当前字母组合是否为单词
  36.   if trie.isWord(str) && !res.contains(str) {
  37.     res.append(str)
  38.   }
  40.   // 继续搜索上下左右四个方向
  41.   visited[i][j] = true
  42.   _dfs(board, m, n, i + 1, j, &visited, &res, trie, str)
  43.   _dfs(board, m, n, i - 1, j, &visited, &res, trie, str)
  44.   _dfs(board, m, n, i, j + 1, &visited, &res, trie, str)
  45.   _dfs(board, m, n, i, j - 1, &visited, &res, trie, str)
  46.   visited[i][j] = false
  47. }

这里对 Trie 不做深入展开，有兴趣的朋友自行研究。

总结

深度优先遍历和广度优先遍历是算法中略微高阶的部分，实际开发中，它也多与地图路径、棋盘游戏相关。虽然不是很常见，但是理解其基本原理并能熟练运用，相信可以使大家的开发功力更上一层楼。

7. 动态规划

之前的章节中，分析的问题大多比较具体直接 —— 可以直接套用一种方法解决。今天要讲的动态规划，其面对的问题通常是无法一蹴而就，需要把复杂的问题分解成简单具体的小问题，然后通过求解简单问题，去推出复杂问题的最终解。
iOS 面试策略之算法基础6-7节 - 图4

形象的理解就是为了推倒一系列纸牌中的第 100 张纸牌，那么我们就要先推倒第 1 张，再依靠多米诺骨牌效应，去推倒第 100 张。

实例讲解

斐波拉契数列是这样一个数列：1, 1, 2, 3, 5, 8, … 除了第一个和第二个数字为 1 以外，其他数字都为之前两个数字之和。现在要求第 100 个数字是多少。

这道题目乍一看是一个数学题，那么要求第 100 个数字，很简单，一个个数字算下去就是了。假设 F(n) 表示第 n 个斐波拉契数列的数字，那么我们易得公式 F(n) = F(n - 1) + F(n - 2)，n >= 2 ，下面就是体力活。当然这道题转化成代码也不是很难，最粗暴的解法如下：

  1. // 此方法会因为栈溢出而崩溃
  2. func Fib() -> Int {
  3.   var (prev, curr) = (0, 1)
  5.   for _ in 1 ..< 100 {
  6.     (curr, prev) = (curr + prev, curr)
  7.   }
  9.   return curr
  10. }

用动态规划怎么写呢？首先要明白动态规划有以下几个专有名词：

1）初始状态，即此问题的最简单子问题的解。在斐波拉契数列里，最简单的问题是，一开始给定的第一个数和第二个数是几？自然我们可以得出是 1；
2）状态转移方程，即第n个问题的解和之前的 n - m 个问题解的关系。在这道题目里，我们已经有了状态转移方程 F(n) = F(n - 1) + F(n - 2)。

所以这题要求 F(100)，那我们只要知道 F(99) 和 F(98) 就行了；想知道 F(99)，我们只要知道 F(98) 和 F(97) 就行了；想要知道 F(98)，我们需要知道 F(97) 和 F(96) …… ，以此类推，我们最后只要知道F(2)和F(1)的值，就可以推出 F(100)。而 F(2) 和 F(1) 正是我们所谓的初始状态，即 F(2) = 1，F(1) =1。所以代码如下：

  1. func Fib(_ n: Int) -> Int {
  2.   // 定义初始状态
  3.   guard n > 0 else {
  4.     return 0
  5.   }
  6.   if n == 1 || n == 2 {
  7.     return 1
  8.   }
  10.   // 调用状态转移方程
  11.   return Fib(n - 1) + Fib(n - 2)
  12. }
  14. print(Fib(100))

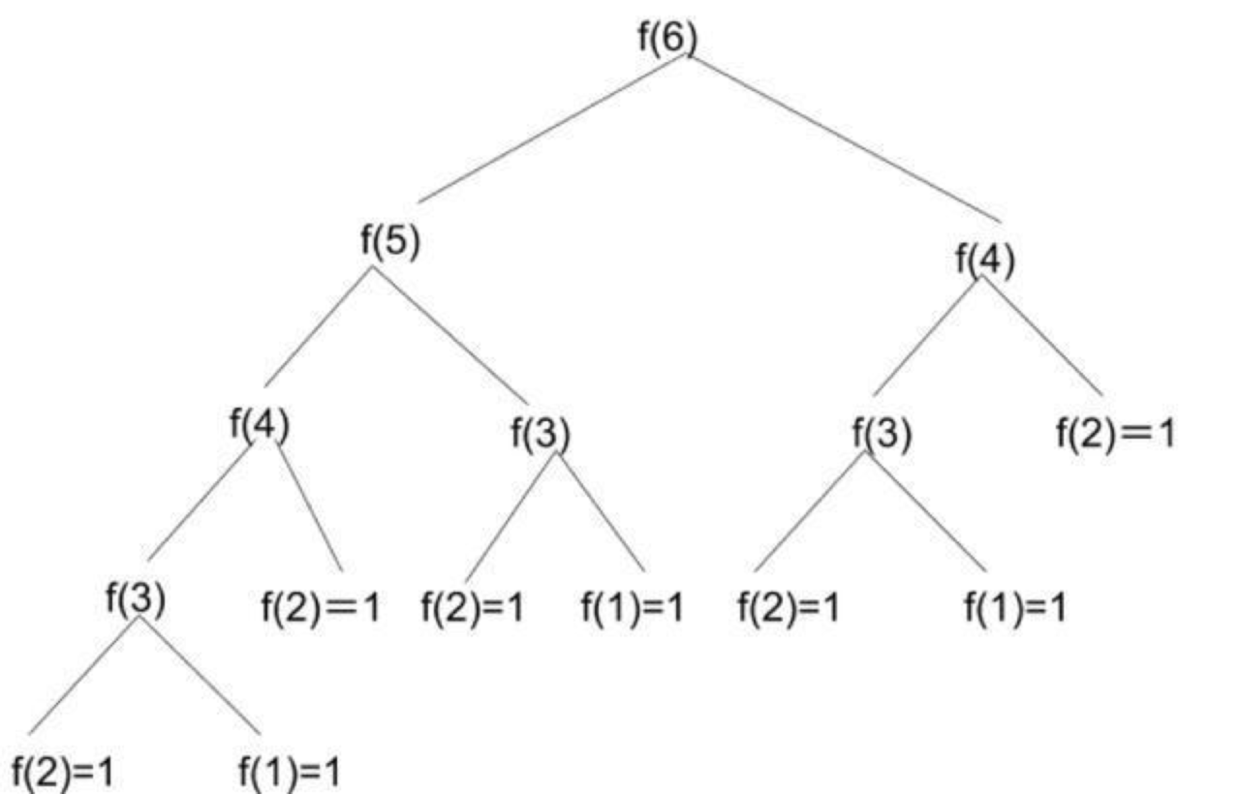
iOS 面试策略之算法基础6-7节 - 图5

这种递归的写法看起来简洁明了，但是上面写法有一个问题：我们要求 F(100)，那么要计算 F(99) 和 F(98) ；要计算 F(99)，我们要计算 F(98) 和 F(97) …… 大家已经发现到这一步，我们已经重复计算两次F(98) 了。而之后的计算中还会有大量的重复，这使得这个解法的复杂度非常之高。解决方法就是，用一个数组，将计算过的值存起来，这样可以用空间上的牺牲来换取时间上的效率提高，代码如下：

  1. var nums = Array(repeating: 0, count: 100)
  3. func Fib(_ n: Int) -> Int {
  4.   // 定义初始状态
  5.   guard n > 0 else {
  6.     return 0
  7.   }
  8.   if n == 1 || n == 2 {
  9.     return 1
  10.   }
  11.   // 如果已经计算过，直接调用，无需重复计算
  12.   if nums[n - 1] != 0 {
  13.     return nums[n - 1]
  14.   }
  16.   // 将计算后的值存入数组
  17.   nums[n - 1] = Fib(n - 1) + Fib(n - 2)
  19.   return nums[n - 1]
  20. }

动态转移虽然看上去十分高大上，但在面试中遇到相关问题要注意以下两点：

  • 栈溢出：每一次递归，程序都会将当前的计算压入栈中。随着递归深度的加深，栈的高度也越来越高，直到超过计算机分配给当前进程的内存容量，程序就会崩溃。
  • 数据溢出：因为动态规划是一种由简至繁的过程，其中积蓄的数据很有可能超过系统 当前数据类型的最大值，从而导致程序抛出异常。

这两点，我们在上面这道求解斐波拉契数列第100个数的题目就都遇到了。

  • 首先，递归的次数很多，我们要从 F(100) = F(99) + F(98) ，一直推理到 F(3) = F(2) + F(1)，这样很容易造成栈溢出。
  • 其次，F(100) 应该是一个很大的数。实际上 F(40) 就已经突破一亿，F(100) 一定会造成整型数据溢出。

当然对于这两点我们也有相应的解决方法。对付栈溢出，我们可以把递归写成循环的形式（所有的递归都可改写成循环）；对付数据溢出，我们可以在程序每次计算中，加入数据溢出的检测，适时终止计算，抛出异常。

斐波拉契数列问题面试实战题

笔者以前在硅谷参加了一个 hackthon 大赛，当时是要做一个扫描英文单词出翻译的 App。它大概长这样：

iOS 面试策略之算法基础6-7节 - 图6

当时这个 App 其他部分运行非常流畅，就是在打开摄像头扫描单词的时候，会出现误读的情况。比如手写的 “price”，机器会识别成 “pr1ce”，从而无法对其进行正确的翻译。笔者对这种情况进行了相应的优化处理，方法如下：

1） 缩小误差范围：将所有的单词构造成前缀树。然后对于扫描的内容，搜索出相应可能的单词。具体做法可以参考上节《深度优先和广度优先》一文中搜索单词的方法。
2） 计算出最接近的单词：假如上一步，我们已经有了10个可能的单词，那么怎么确定最接近真实情况的单词呢？这里我们要定义两个单词的距离 — 从第一个单词wordA，到第二个单词wordB，有三种操作：

  • 删除一个字符
  • 添加一个字符
  • 替换一个字符

综合上述三种操作，用最少步骤将单词wordA变到单词wordB，我们就称这个值为两个单词之间的距离。比如 pr1ce -> price，只需要将 1 替换为 i 即可，所以两个单词之间的距离为1。pr1ce -> prize，要将 1 替换为 i ，再将 c 替换为 z ，所以两个单词之间的距离为2。相比于prize，price更为接近原来的单词。

现在问题转变为实现下面这个方法：

  1. func wordDistance(_ wordA: String, wordB: String) -> Int { ... }

要解决这个复杂的问题，我们不如从一个简单的例子出发：求 “abce” 到 “abdf” 之间的距离。它们两之间的距离，无非是下面三种情况中的一种。

  • 删除一个字符：假如已知 wordDistance("abc", "abdf") ，那么 “abce” 只需要删除一个字符到达 “abc” ，然后就可以得知 “abce” 到 “abdf” 之间的距离。
  • 添加一个字符：假如已知 wordDistance("abce", "abd")，那么我们只要让 “abd” 添加一个字符到达 “abdf” 即可求出最终解。
  • 替换一个字符：假如已知 wordDistance("abc", "abd")，那么就可以依此推出wordDistance("abce", "abde") = wordDistance("abc", "abd")。故而只要将末尾的 “e” 替换成 “f”，就可以得出 wordDistance("abce", "abdf")。

这样我们就可以发现，求解任意两个单词之间的距离，只要知道之前单词组合的距离即可。我们用dp[i][j]表示第一个字符串 wordA[0…i] 和第 2 个字符串 wordB[0…j] 的最短编辑距离，那么这个动态规划的两个重要参数分别是：

  • 初始状态：dp[0][j] = j，dp[i][0] = i
  • 状态转移方程：dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1

再举例解释一下，”abc” 到 “xyz”，dp[2][1] 就是 “ab” 到 “x” 的距离，不难看出是 2；dp[1][2] 就是 “a” 到 “xy” 的距离，是 2；dp[1][1] 也就是 “a” 到 “x” 的距离，很显然就是 1。所以 dp[2][2] 即 “ab” 到 “xy” 的距离是 min(dp[2][1], dp[1][2], dp[1][1]) + 1 就是 2。

有了初始状态和状态转移方程，那么动态规划的代码就出来了：

  1. func wordDistance(_ wordA: String, _ wordB: String) -> Int {
  2.   let aChars = Array(wordA), bChars = Array(wordB)
  3.   let aLen = aChars.count, bLen = bChars.count
  5.   var dp = Array(repeating: (Array(repeating: 0, count: bLen + 1)), count: aLen + 1)
  7.   for i in 0 ... aLen {
  8.     for j in 0 ... bLen {
  9.       // 初始情况
  10.       if i == 0 {
  11.         dp[i][j] = j
  12.       } else if j == 0 {
  13.         dp[i][j] = i
  14.       // 特殊情况
  15.       } else if aChars[i - 1] == bChars[j - 1] {
  16.         dp[i][j] = dp[i - 1][j - 1]
  17.       } else {
  18.         // 状态转移方程
  19.         dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1
  20.       }
  21.     }
  22.   }
  24.   return dp[aLen][bLen]
  25. }

用动态规划计算出单词之间的距离之后，在做一些相应的优化，就可以准确的识别出扫描的单词。

总结

动态规划算是算法进阶中比较重要的一环，它的思想就是把复杂问题化为简单具体问题，然后分析出初始状态和状态转移方程，从而推出最终解。也许它在实际编程或是 iOS 开发中出现频率不高，但是这种删繁就简的思路，却可以应用在生活或者工作中的方方面面。

推荐👇：

如果你正在跳槽或者正准备跳槽不妨动动小手，添加一下咱们的交流群931 542 608来获取一份详细的大厂面试资料为你的跳槽多添一份保障。

iOS 面试策略之算法基础6-7节 - 图7