是什么？

工作原理是每一趟从待排序的数据元素中选出最小（或最大）的一个元素，顺序放在已排好序的数列的最后（或最后），直到全部待排序的数据元素排完。

原理是什么？

1. 从原始的数组中找到最小（或者最大）的元素，然后将找到的元素和第1（或者n）的元素交互。
2. 接着从剩余n-1个数中找到最小（或者最大）的元素，然后在将找到的元素和弟2（或者n-1）的元素交换。
3. 不断重复上面的动作，直到最后两个数交互完成。

   时间复杂度、空间复杂度和稳定性

   选择排序的时间复杂度是 O(N2) ：假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N)，需要遍历多少次呢？N-1次，因此，选择排序的时间复杂度是 O(N2)。空间复杂度是 O(1)。
   选择排序是不稳定的算法，举个例子：数组 6、7、6、2、8，在对其进行第一遍循环的时候，会将第一个位置的6与后面的8进行交换。此时，就已经将两个6的相对前后位置改变了。因此选择排序不是稳定性排序算法。

   算法稳定不稳定定义：假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！

常规实现

function selectSort(arr) {
  let length = arr.length,
      j;
  if (length < 2) return arr;
  for (let i = 0; i < length - 1; i ++) {
    let maxIndex = i;
    for (let j = i + 1; j < length; j++) {
      if (arr[maxIndex] < arr[j]) {
        maxIndex = j;
      }
    }
    [arr[maxIndex], arr[i]] = [arr[i], arr[maxIndex]];
  }
  return arr;
}

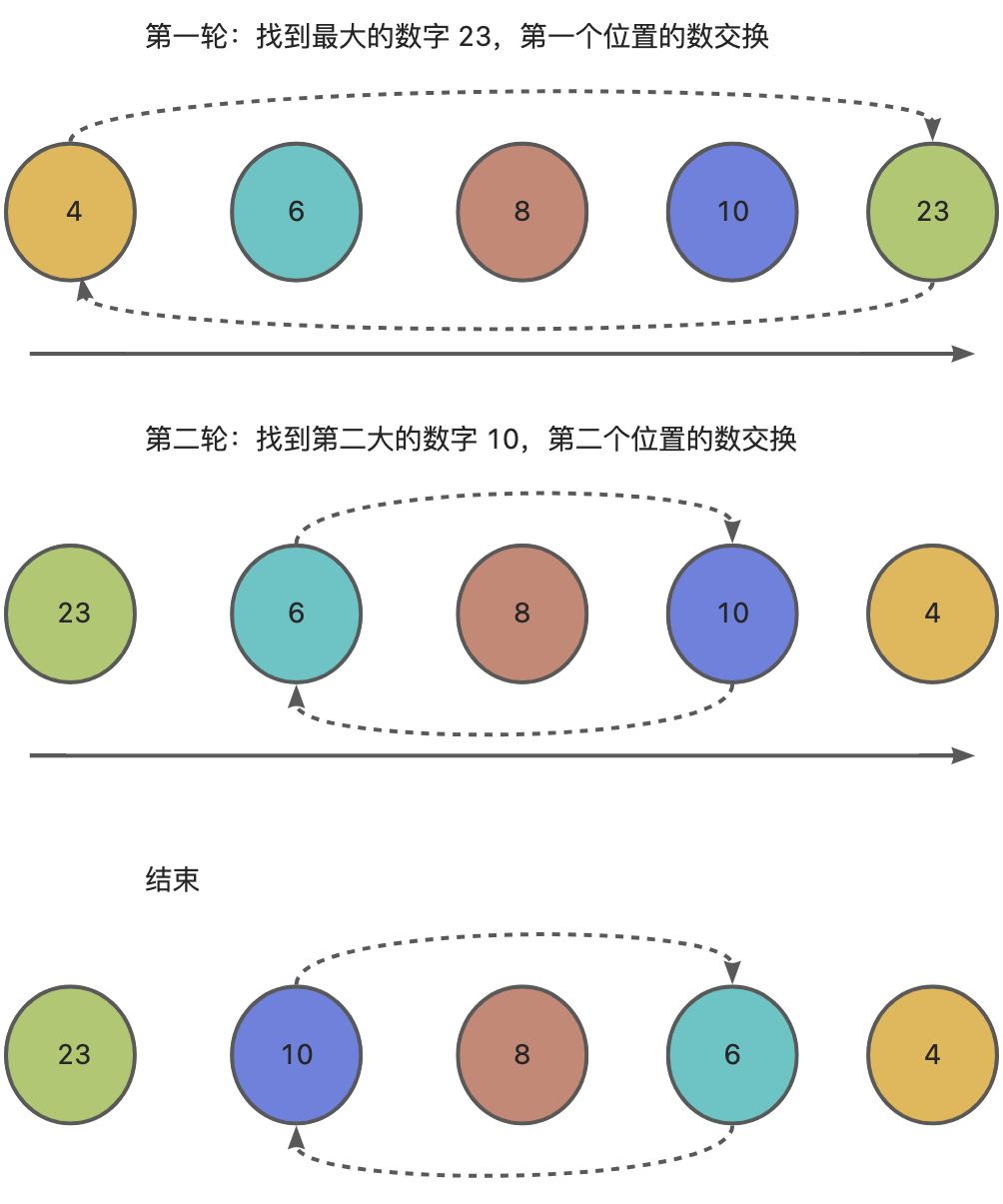
比如：有数列 [4, 6, 8, 10, 23]。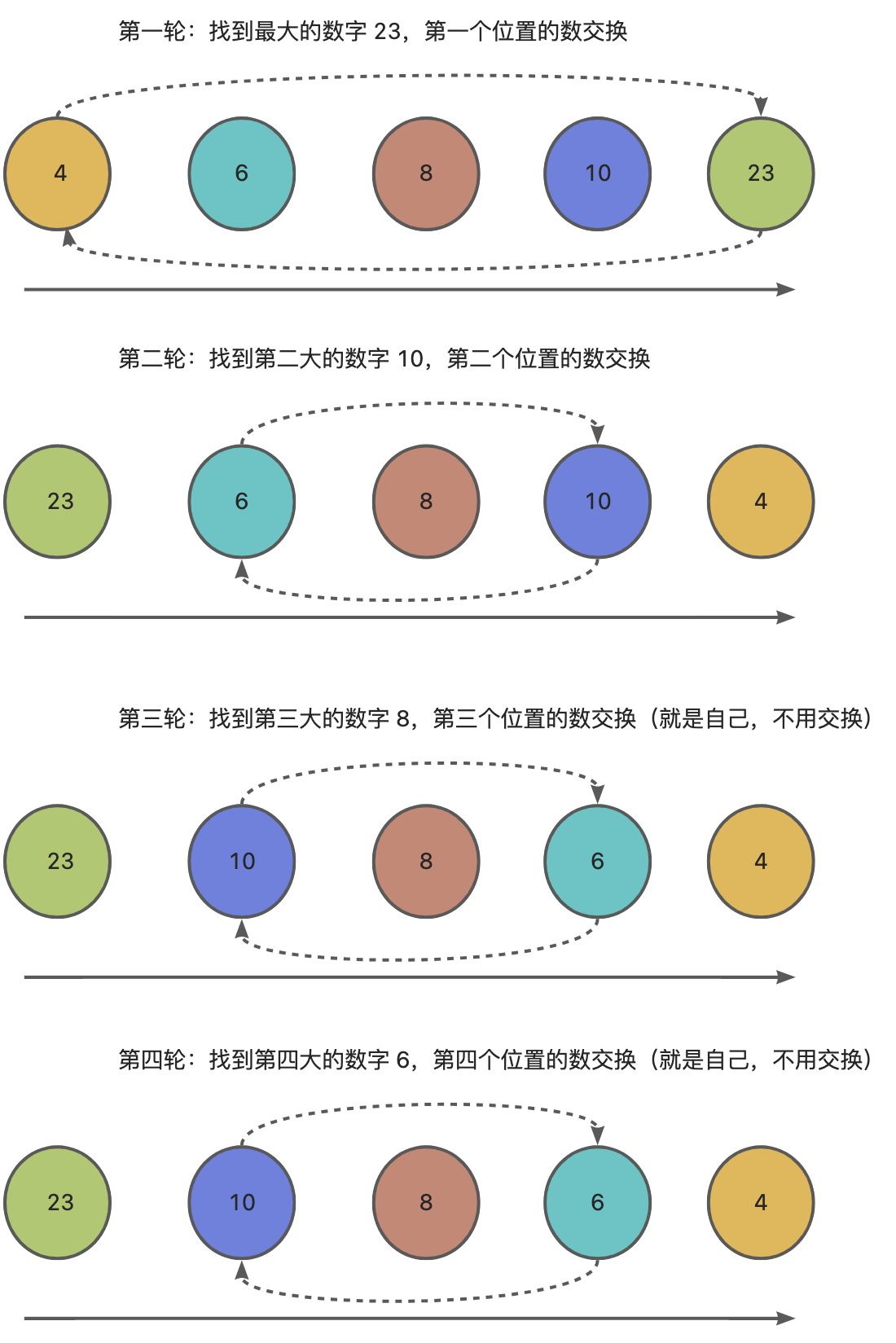

但是发现在整个过程的第三轮和第四轮中，发现最大的树就是当前本身，不需要进行交互。所以这里可以小小的优化一下。判断一下如果当前最大的数字的下标就是自己，就不用做交换操作了。

function selectSort(arr) {
  let length = arr.length,
      j;
  if (length < 2) return arr;
  for (let i = 0; i < length - 1; i ++) {
    let maxIndex = i;
    for (let j = i + 1; j < length; j++) {
      if (arr[maxIndex] < arr[j]) {
        maxIndex = j;
      }
    }
    if (maxIndex !== i) {
      [arr[maxIndex], arr[i]] = [arr[i], arr[maxIndex]];
    }
  }
  return a;
}