俗话说，面试造火箭🚀，工作拧螺丝🔩。在面试中，算法一定会考，在拧螺丝时却不一定会用，但是排序我相信大家或多或少都会用到。
今天给大家详细的再讲讲冒泡排序，升级在升级的版本。

是什么？

冒泡排序（Bubble Sort），是一种较简单的排序算法。它重复地走访过要排序的元素列，依次比较两个相邻的元素，如果顺序（如从大到小、首字母从Z到A）错误就把他们交换过来。走访元素的工作是重复地进行，直到没有相邻元素需要交换，也就是说该元素列已经排序完成。
这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端（升序或降序排列），就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样，故名“冒泡排序”。

原理是什么？

冒泡排序每一趟比较都只能确定一个数归位（归到指定的位置）。如果是升序排列，那么第一趟就只能确认末尾上的数，第二趟只能确认倒数第二位上的数，依次类推。如果有n 个数需要排序，只需要进行 n - 1 趟排序。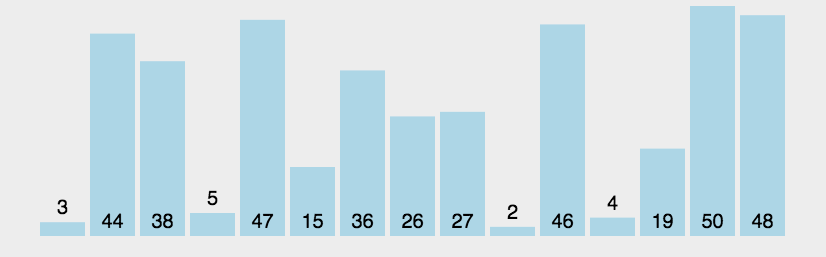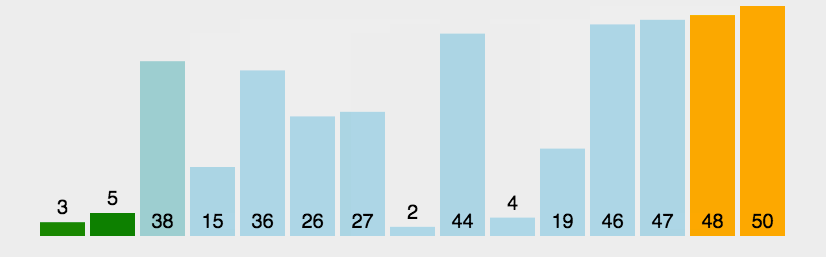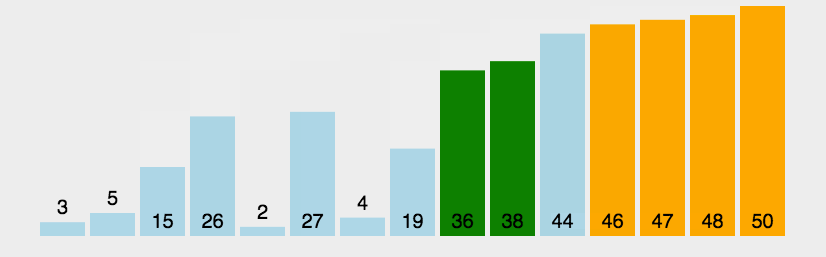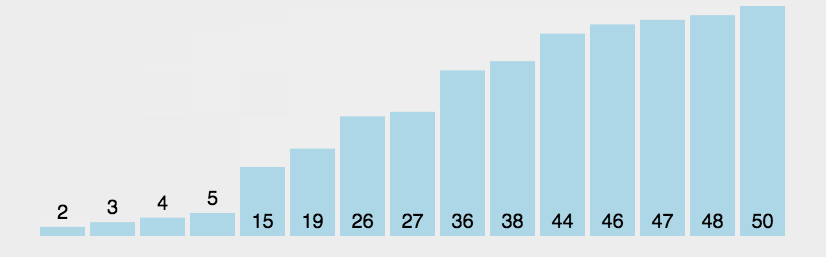
冒泡排序.gif

时间复杂度

如果排序对象有 n 个数字需要排序n - 1趟，
第一趟需要n - 1次比较，
第二趟需要n - 2次比较，
第三趟需要 n - 3次比较，
依次类推，（n-1）+ (n-2) + (n-3)+...+3+2+1 = n(n-1)/2 = 1/2 _*n__2__ - 1/2 * _n。
根据复杂度的规则，去掉低阶项（也就是 n/2），并去掉常数系数，那复杂度就是 O(n^2)了；冒泡排序也是一种稳定排序，因为在两个数交换的时候，如果两个数相同，那么它们并不会因为算法中哪条语句相互交换位置。

常规版本

function bubbleSort(arr) {
  const length = arr.length;
  if (!length) return arr;
  for (let i = 0; i < length; i++) {
    for (let j = 0; j < length - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
      }
    }
  }
  return arr;
}
let array = [];
for (let i = 0; i < 10; i++) {
  let number = Math.floor(Math.random() * 10);
  array.push(number);
}
var arrSorted = bubbleSort(array);
console.log(arrSorted);

这种最常规的版本，我相信你一定见过，第一层循环是用来控制趟数，也就是 n 个数就要比较 n-1 趟；第二层是控制第 i + 1 趟（因为循环中 i 是从 0 开始的）的比较次数，那么 i+1 趟就是比较了 N-1-i。

这里有一个小问题，如果在执行的过程中，在**某一趟比较完成之后，发现整个数列已经有序了**，如果还是按照上面的代码，还是会进行接下来的比较，这样其实在会有很多无效的比较。是不是可以优化一下了？

升级版本

function bubbleSort2(arr) {
  const length = arr.length;
  if (!length) return arr;
  for (let i = 0; i < length; i++) {
    let mark = true;
    for (let j = 0; j < length - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
        mark = false;
      }
    }
    if (mark) break;
  }
  return arr;
}
let array = [];
for (let i = 0; i < 10; i++) {
  let number = Math.floor(Math.random() * 10);
  array.push(number);
}
var arrSorted = bubbleSort(array);
console.log(arrSorted);

优化其实也很简单，就是将上面代码做一点点小小改动即可，也就是利用 mark作为标记。如果在本轮排序中，元素有交换，则说明数列无序；如果没有元素交换，说明数列已然有序，直接跳出大循环。
这种优化就是当在排序的过程中，在本趟的排序``某一轮中如果整个数列已经有序，就不需要进行剩下的趟排序了，直接结束就行。
优化完的排序在数据量比较少的情况下，并不能显示出什么优化。

注意：排序算法性能比较都以实际情况为准。

但是如果数据量比较大的情况，你就会看到明显的差异。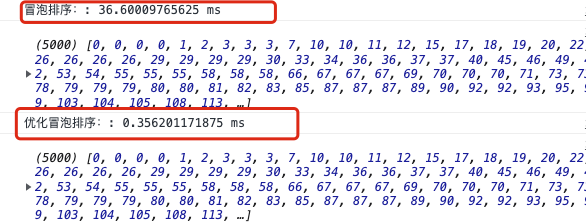

注意：排序算法性能比较都以实际情况为准。

这里还有一种情况是，**如果数列一半是有序的，一半是无序的，比如，数列的前半部分是有序的，后半部分是无序的，**其实后面的许多元素已经是有序的了，但是每一轮还是白白比较了许多次呢？是不是可以优化一下了。

再升级版本

关键的优化点在于数列有序区的界定。如果按冒泡排序代码原始版来分析的话，有序区的长度和排序的轮数是相等的。比如：第一趟排序过后的有序区长度是1，第二趟排序过后的有序区长度是2，第三趟排序过后的有序区长度是3 ……。但是这并不完全正确，实际数列真正的有序区可能会大于这个长度，因为数列可能原本已经存在部分有序。在种情况下，我们如果来避免这种情况了？其实我们可以**在每一轮排序的最后，记录一下最后一次元素交换的位置，那个位置也就是无序数列的边界，再往后就是有序区了**。

function bubbleSort3(arr) {
  const length = arr.length;
  if (!length) return arr;
  // 无序边界
  let boundary = length - 1;
  // 记录最后一次交换位置
  let lastExIndex = 0;
  for (let i = 0; i < length; i++) {
    let mark = true;
    for (let j = 0; j < boundary; j ++) {
      if (array[j] > arrya[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
        lastExIndex = j;
        mark = false;
      }
    }
    boundary = lastExIndex;
    if (mark) break;
  }
}
let array = [];
for (let i = 0; i < 10; i++) {
  let number = Math.floor(Math.random() * 10);
  array.push(number);
}
var arrSorted = bubbleSort(array);
console.log(arrSorted);

在数据量比较的情况下，性能还不是很明显哈。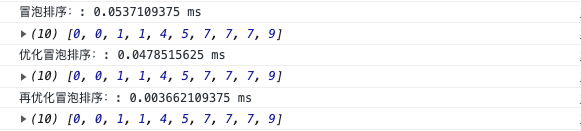

但是大数据下的性能相对常规版本还是比较明显的。

注意：排序算法性能比较都以实际情况为准。

最后

本文通过优化版本、再优化版本，优化冒泡排序本身的性能，为算法提速，希望在工作中、在面试中，能被你利用起来，本文到此结束，如有问题评论区或者私信和我交流。

前端进阶，准备好才不会被淘汰

冒泡排序升级，再升级（超详细）

是什么？

原理是什么？

时间复杂度

常规版本

升级版本

再升级版本

最后