实验目的

1.理解朴素贝叶斯的原理
2.掌握scikit-learn贝叶斯的用法
3.认识可视化工具seaborn

实验原理

1.分类问题描述

贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。而朴素贝叶斯分类是贝叶斯分类中最简单，也是常见的一种分类方法，对于分类问题，其实谁都不会陌生，日常生活中我们每天都进行着分类过程。例如，当你看到一个人，你的脑子下意识判断他是学生还是社会上的人；你可能经常会走在路上对身旁的朋友说“这个人一看就很有钱”之类的话，其实这就是一种分类操作，贝叶斯分类算法，那么分类的数学描述又是什么呢？
1.6 机器学习——朴素贝叶斯 - 图1
其中C叫做类别集合，其中每一个元素是一个类别，而I叫做项集合（特征集合），其中每一个元素是一个待分类项，f叫做分类器。分类算法的内容是要求给定特征，构造分类器f，让我们得出类别。

2.Bayes’ theorem(贝叶斯法则)

在概率论和统计学中，Bayes theorem（贝叶斯法则）根据事件的先验知识描述事件的概率。贝叶斯法则表达式如下所示：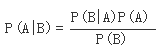
1.6 机器学习——朴素贝叶斯 - 图2

  • P(A|B) – 在事件B下事件A发生的条件概率
  • P(B|A) – 在事件A下事件B发生的条件概率
  • P(A), P(B) – 独立事件A和独立事件B的边缘概率

朴素贝叶斯方法是一组监督学习算法，它基于贝叶斯定理应用每对特征之间的“天真”独立假设。给定类变量y和从属特征矢量X1通过Xn，贝叶斯定理状态下列关系式：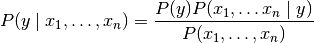
1.6 机器学习——朴素贝叶斯 - 图3
使用天真的独立假设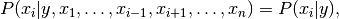
1.6 机器学习——朴素贝叶斯 - 图4
对所有人来说i，这种关系简化为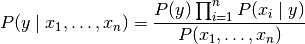
1.6 机器学习——朴素贝叶斯 - 图5
由于
1.6 机器学习——朴素贝叶斯 - 图6
输入是常数，我们可以使用以下分类规则：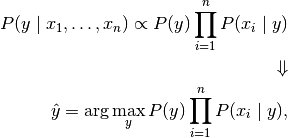
1.6 机器学习——朴素贝叶斯 - 图7
我们可以使用最大后验（MAP）估计来估计的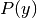
1.6 机器学习——朴素贝叶斯 - 图8
和
1.6 机器学习——朴素贝叶斯 - 图9
；前者是y 训练集中类的相对频率。
不同的朴素贝叶斯分类器主要区别于他们对分布的假设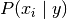
1.6 机器学习——朴素贝叶斯 - 图10

3.朴素贝叶斯分类算法

在scikit-learn中，提供了3种朴素贝叶斯分类算法：GaussianNB(高斯朴素贝叶斯)、MultinomialNB(多项式朴素贝叶斯)、BernoulliNB(伯努利朴素贝叶斯)
可以参考文档：
http://scikit-learn.org/stable/modules/naive_bayes.html
http://scikit-learn.org/stable/modules/generated/sklearn.naive_bayes.GaussianNB.html

实验内容

利用scikit-learn提供的三种朴素贝叶斯算法，构建分类器，根据花瓣花萼的宽度和长度判断他们属于哪一类

实验环境

Linux Ubuntu 16.04
Python 3.6.1
Jupyter

实验步骤

1.首先打开终端模拟器，切换到/data目录，下载所需资源：

  1. cd /data  
  2. wget http://192.168.1.100:60000/allfiles/sklearn/logic/iris.csv

输入下面命令：

  1. jupyter notebook --ip='127.0.0.1'

如果是第一次打开，浏览器界面会要求输入密码，密码为zhangyu，如图所示：
1.6 机器学习——朴素贝叶斯 - 图11
2.切换到/data目录下，点击New，在其下拉框中选择folder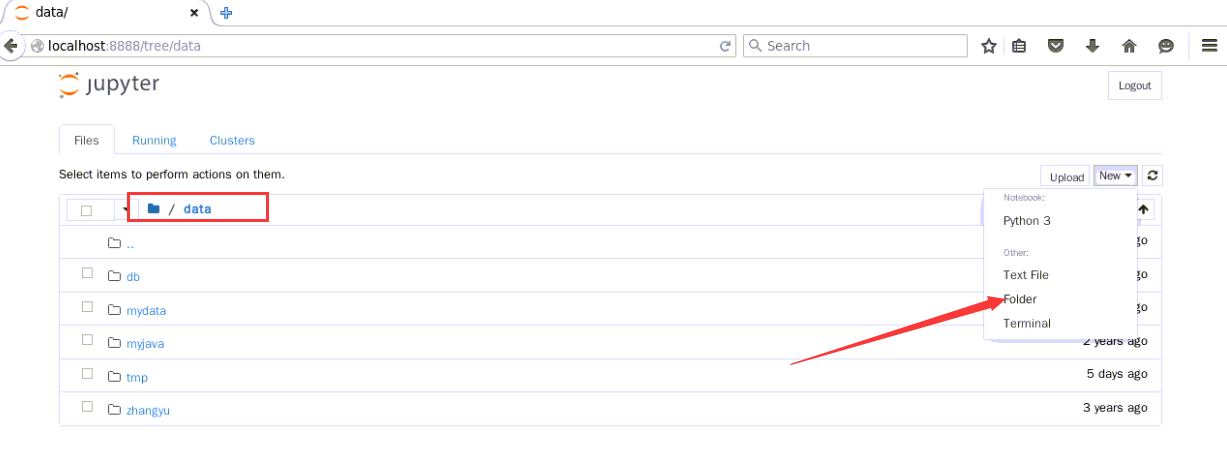
1.6 机器学习——朴素贝叶斯 - 图12
选中刚才创建的文件夹，点击页面左上角的【Rename】
1.6 机器学习——朴素贝叶斯 - 图13
重命名为naivebytes
1.6 机器学习——朴素贝叶斯 - 图14
3.切换到naivebytes目录下，新建一个ipynb文件，用于编写并执行代码。点击页面右上角的New，选中【Python3】
1.6 机器学习——朴素贝叶斯 - 图15
新建ipynb文件如下所示，在此可以编写代码了
1.6 机器学习——朴素贝叶斯 - 图16
4.朴素贝叶斯
贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。而朴素贝叶斯分类是贝叶斯分类中最简单，也是常见的一种分类方法

(1)业务理解

先有一张表格，描述了花瓣的特征和种类，利用scikit-learn提供的三种朴素贝叶斯算法，构建分类器，根据花瓣花萼的宽度和长度预测他们属于哪一个品种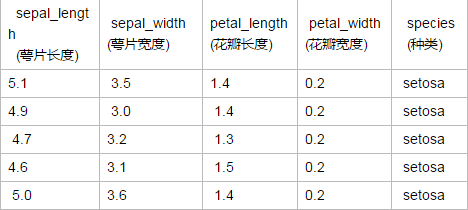
1.6 机器学习——朴素贝叶斯 - 图17

(2)读取数据

2.1.在刚才新建的ipynb文件中，编写代码，读取数据

  1. #导入pandas库和numpy库
  2. import pandas as pd  
  3. import numpy as np  
  4. iris = pd.read_csv('/data/iris.csv') 
  5. iris.head()

点击如下所示按钮，运行文件
1.6 机器学习——朴素贝叶斯 - 图18

2.2.运行结果如下所示：

1.6 机器学习——朴素贝叶斯 - 图19

（3）数据理解

3.1.查看数据结构

1.6 机器学习——朴素贝叶斯 - 图20
说明：该数据总共有150行，5列

3.2.查看数据列名称

1.6 机器学习——朴素贝叶斯 - 图21

（4）数据准备

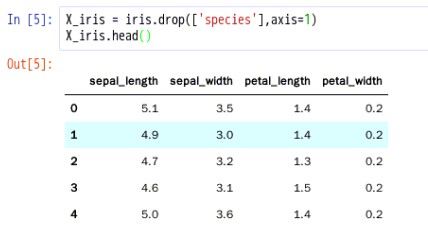
4.1.删除“种类”这列数据得到特征数据如下：

1.6 机器学习——朴素贝叶斯 - 图22

4.2.获取“species”这列数据并将其转换为数组，得到预测数据

1.6 机器学习——朴素贝叶斯 - 图23
查看y_iris总共有多少行
1.6 机器学习——朴素贝叶斯 - 图24

4.3.构建训练和测试数据集

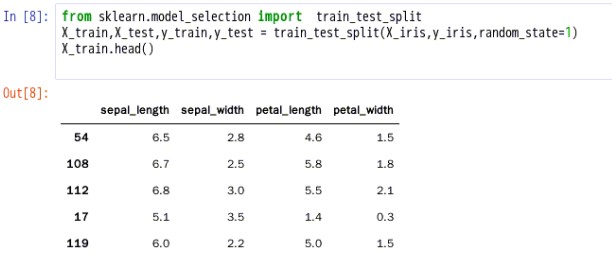
1.6 机器学习——朴素贝叶斯 - 图25
说明：将数据分为训练集和测试集，默认情况下，75%的数据用于训练，25%的数据用于测试

  • 训练集是用于发现和预测潜在关系的一组数据。
  • 测试集是用于评估预测关系强度和效率的一组数据。

    4.4.查看训练集和测试集的数据结构

    1.6 机器学习——朴素贝叶斯 - 图26
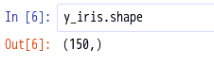
    说明：训练集：X_iris数据为(150,4)，X_train为(112,4)，X_test为(38,4)
    sales数据为200行，y_train为(112,)，y_test为（38,）

    4.5.查看y_train数据

    1.6 机器学习——朴素贝叶斯 - 图27

    （5）模型构建

    在scikit-learn中，提供了3种朴素贝叶斯分类算法：GaussianNB(高斯朴素贝叶斯)、MultinomialNB(多项式朴素贝叶斯)、BernoulliNB(伯努利朴素贝叶斯)
    GaussianNB实现高斯朴素贝叶斯算法进行分类。假设特征的可能性是高斯的：
    1.6 机器学习——朴素贝叶斯 - 图28

    《一、GaussianNB(高斯朴素贝叶斯)》

    5.1.利用GaussianNB类建立简单模型并预测

    1.6 机器学习——朴素贝叶斯 - 图29

    5.2.构建一个新的测试数组

    1.6 机器学习——朴素贝叶斯 - 图30

    5.3.将测试数据带入模型预测得到预测结果

    1.6 机器学习——朴素贝叶斯 - 图31
    说明：当我们提供的数据为’sepal_length’:[‘5’],’sepal_width’:[‘3’],’petal_length’:[‘3’],’petal_width’:[‘1.8’]时，预测它属于‘versicolor’这个种类，到底预测正确与否呢？接下来看一下预测结果的平均值

    5.4.查看预测结果的平均值

    1.6 机器学习——朴素贝叶斯 - 图32
    mean()函数功能：求取均值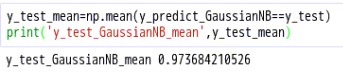
    1.6 机器学习——朴素贝叶斯 - 图33

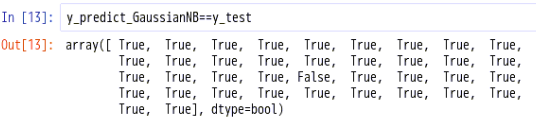
    5.5.查看预测正确率

    score(X, y[, sample_weight]) 返回给定测试数据和标签的平均精度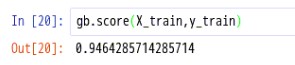
    1.6 机器学习——朴素贝叶斯 - 图34

    《二、BernoulliNB(伯努利朴素贝叶斯) 》

    BernoulliNB实现了根据多元伯努利分布的数据的朴素贝叶斯训练和分类算法; 即，可能存在多个特征，但每个特征被假定为二进制值（伯努利，布尔）变量。因此，该类要求将样本表示为二进制值特征向量；如果传递任何其他类型的数据，BernoulliNB实例可以将其输入二值化（取决于binarize参数）。
    伯努利朴素贝叶斯的决策规则是基于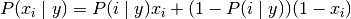
    1.6 机器学习——朴素贝叶斯 - 图35
    5.6.利用BernoulliNB类建立简单模型并预测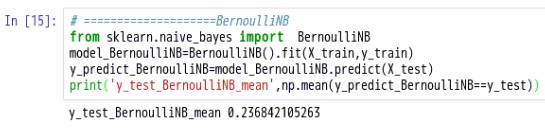
    1.6 机器学习——朴素贝叶斯 - 图36

    《三、MultinomialNB(多项式朴素贝叶斯)》

    MultinomialNB实现用于多项分布数据的朴素贝叶斯算法，并且是用于文本分类的两种经典朴素贝叶斯变体之一（其中数据通常表示为单词向量计数，尽管tf-idf向量也已知在实践中很好地工作） 。通过
    1.6 机器学习——朴素贝叶斯 - 图37
    每个类的向量对分布进行参数化y,其中n是特征的数量（在文本分类中，词汇的大小），并且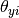
    1.6 机器学习——朴素贝叶斯 - 图38
    是在属于类的样本中出现
    1.6 机器学习——朴素贝叶斯 - 图39
    特征的概率。
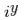
    1.6 机器学习——朴素贝叶斯 - 图40
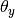
    1.6 机器学习——朴素贝叶斯 - 图41
    通过平滑版本的最大似然估计参数，即相对频率计数：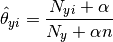
    1.6 机器学习——朴素贝叶斯 - 图42
    这里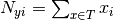
    1.6 机器学习——朴素贝叶斯 - 图43
    是次数的功能i出现类样本中y训练集中T，并且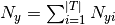
    1.6 机器学习——朴素贝叶斯 - 图44
    平滑先验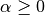
    1.6 机器学习——朴素贝叶斯 - 图45
    考虑了学习样本中不存在的特征，并防止了进一步计算中的零概率。设置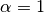
    1.6 机器学习——朴素贝叶斯 - 图46
    称为拉普拉斯平滑，而
    1.6 机器学习——朴素贝叶斯 - 图47
    称为Lidstone平滑。

    5.7.利用MultinomialNB类建立简单模型并预测

    1.6 机器学习——朴素贝叶斯 - 图48
    至此，实验结束！