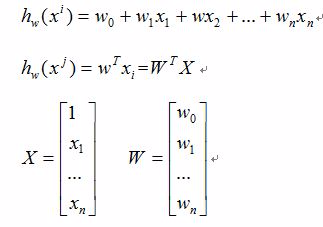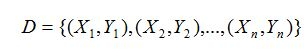实验目的

1.理解多元线性回归模型原理
2.掌握scikit-learn关于线性回归模型的处理
3.掌握模型评估方式
4.掌握数据可视化方法

实验原理

《一、线性回归》

在现实生活中普遍存在着变量之间的关系，有确定的和非确定的。确定关系指的是变量之间可以使用函数关系式表示，还有一种是属于非确定的（相关），比如人的身高和体重，一样的身高可能体重是不一样的。他们之间存在着一定的关系，下面我们先来看一下线性回归概念
线性回归：

1. 函数模型（Model）：

1.2 机器学习——多元线性回归 - 图1
假设有训练数据
1.2 机器学习——多元线性回归 - 图2
那么为了方便我们写成矩阵的形式
1.2 机器学习——多元线性回归 - 图3

2.损失函数（cost）：现在我们需要根据给定的X求解W的值，这里采用最小二乘法。

何为最小二乘法，其实很简单。我们有很多的给定点，这时候我们需要找出一条线去拟合它，那么我先假设这个线的方程，然后把数据点代入假设的方程得到观测值，求使得实际值与观测值相减的平方和最小的参数。对变量求偏导联立便可求，因此损失代价函数为：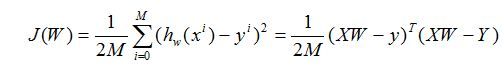
1.2 机器学习——多元线性回归 - 图4

《二、scikit-learn》

在机器学习和数据挖掘的应用中，scikit-learn是一个功能强大的python包。在数据量不是过大的情况下，可以解决大部分问题，这里介绍几个概念

估计器（Estimator）

估计器，很多时候可以直接理解成分类器，主要包含两个函数：
fit()：训练算法，设置内部参数。接收训练集和类别两个参数。
predict()：预测测试集类别，参数为测试集。
大多数scikit-learn估计器接收和输出的数据格式均为numpy数组或类似格式。

模型评估（度量）

包：sklearn.metrics
sklearn.metrics包含评分方法、性能度量、成对度量和距离计算。

回归结果度量

  • explained_varicance_score：可解释方差的回归评分函数
  • mean_absolute_error：平均绝对误差

  • mean_squared_error：平均平方误差

    实验内容

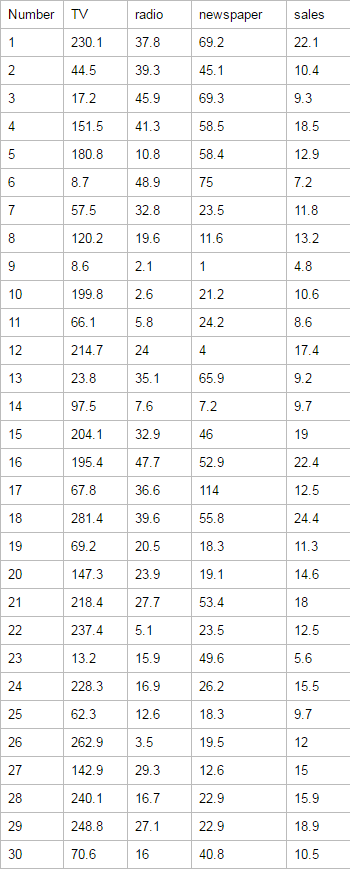
    样本数据如下（列举一部分），我们通过不同的广告投入，预测产品销量
    1.2 机器学习——多元线性回归 - 图5

    实验环境

    Linux Ubuntu 16.04
    Python 3.6.1
    Jupyter

    实验步骤

    1.首先打开终端模拟器，输入下面命令：jupyter notebook —ip=’127.0.0.1’，

    1. cd /  
    2. jupyter notebook --ip='127.0.0.1'

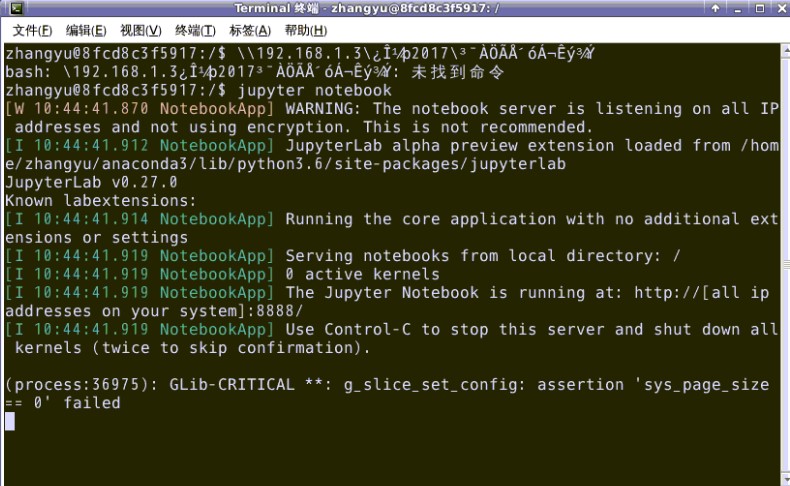
    1.2 机器学习——多元线性回归 - 图6
    如上图所示，该终端不要关闭，在浏览器中会打开下面界面，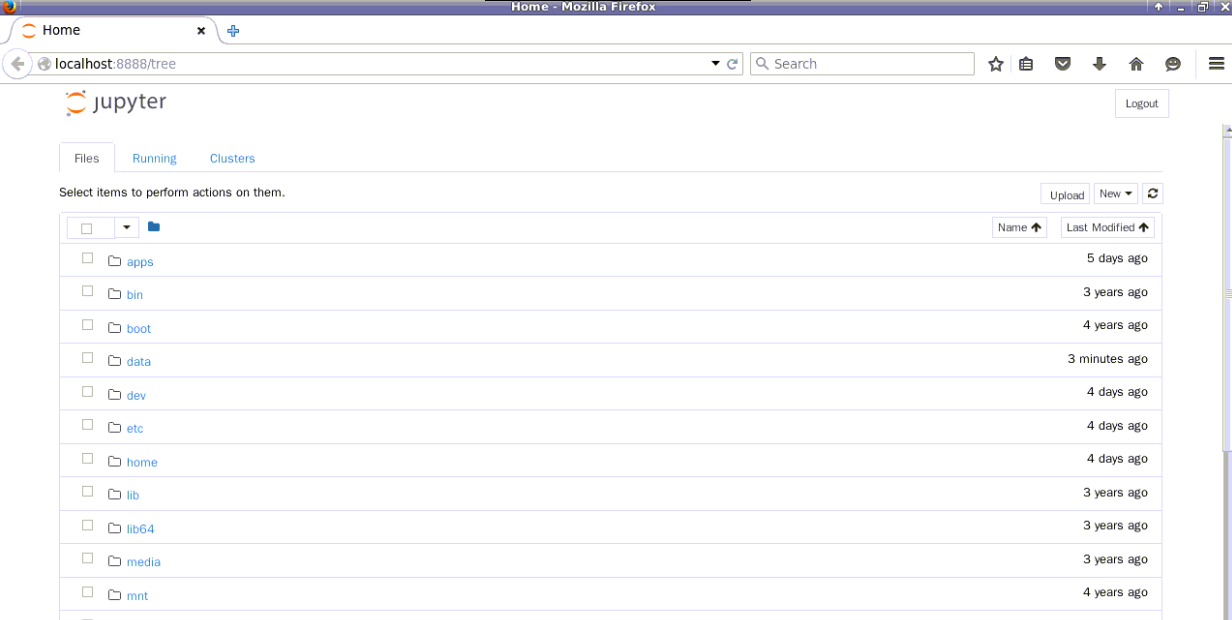
    1.2 机器学习——多元线性回归 - 图7
    如果是第一次打开，浏览器界面会要求输入密码，密码为zhangyu
    2.切换到/data目录下，点击New，在其下拉框中选择folder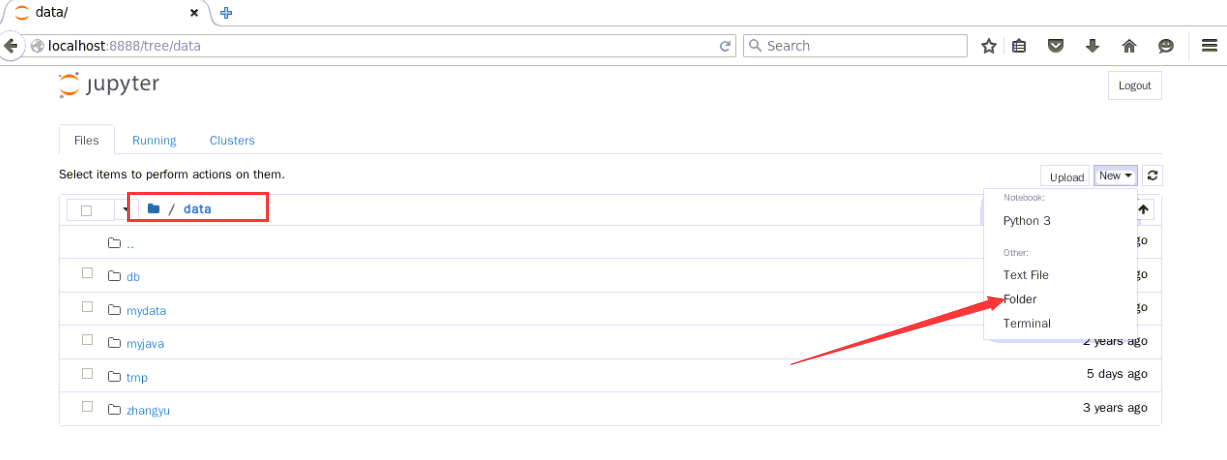
    1.2 机器学习——多元线性回归 - 图8
    选中刚才创建的文件夹，点击页面左上角的【Rename】
    1.2 机器学习——多元线性回归 - 图9
    重命名为m_linear_regression
    1.2 机器学习——多元线性回归 - 图10
    3.切换到m_linear_regression 目录下，新建一个ipynb文件，用于编写并执行代码。点击页面右上角的New，选中【Python3】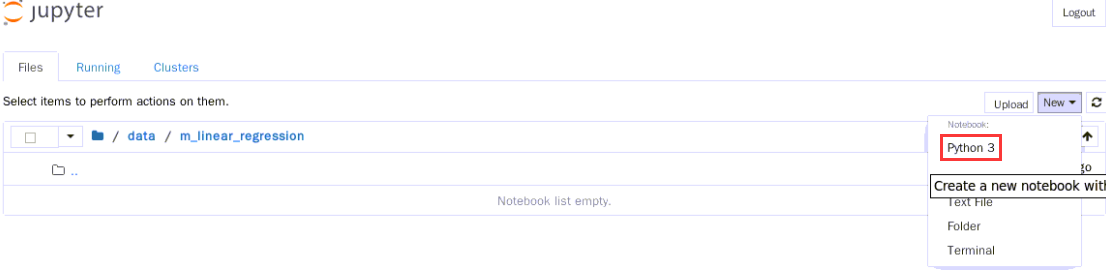
    1.2 机器学习——多元线性回归 - 图11
    新建ipynb文件如下所示，在此可以编写代码了
    1.2 机器学习——多元线性回归 - 图12
    4.多元线性回归分析
    在统计学中，线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归，大于一个自变量情况的叫做多元回归。
    我们将通过以下9个步骤开始学习多元线性回归
    1.业务理解
    2.读取数据
    3.数据理解
    4.数据准备
    5.构建线性回归模型
    6.模型预测
    7.模型评价

    （1）业务理解

    现有一张产品不同广告渠道的销量汇总表
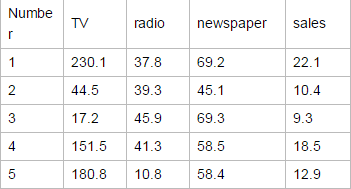
    1.2 机器学习——多元线性回归 - 图13
    特征：
    TV：对于一个给定市场中单一产品，用于电视上的广告费用（以千为单位）
    Radio：在广播媒体上投资的广告费用
    Newspaper：用于报纸媒体的广告费用
    响应：
    Sales：对应产品的销量
    现在要分析Sales和TV、Radio、Newspaper多个变量之间的关系，即多元线性回归分析

    （2）获取数据并读取数据

    打开linux终端，下载所需资源m_ linear_regression 

    1. cd /data/m_linear_regression  
    2. wget http://192.168.1.100:60000/allfiles/sklearn/line/Advertising.csv

    1.2 机器学习——多元线性回归 - 图14
    在刚才新建的ipynb文件中，编写代码，使用pandas来读取数据，Pandas是一个用于数据探索、数据处理、数据分析的Python库

    1. #导入pandas库和numpy库
    2. import pandas as pd  
    3. import numpy as np  
    4. #读取women.csv
    5. data= pd.read_csv('Advertising.csv', header=0)  
    6. #读取前五行数据，如果是最后五行，用df_women.tail()
    7. data.head()

    点击如下所示按钮，运行文件
    1.2 机器学习——多元线性回归 - 图15
    运行结果如下所示：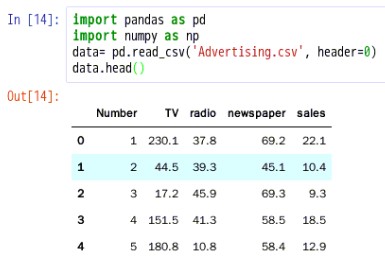
    1.2 机器学习——多元线性回归 - 图16
    上面显示的结果类似一个电子表格，这个结构称为Pandas的数据帧(data frame)。
    pandas的两个主要数据结构：Series和DataFrame：

  • Series类似于一维数组，它有一组数据以及一组与之相关的数据标签(即索引)组成。

  • DataFrame是一个表格型的数据结构，它含有一组有序的列，每列可以是不同的值类型。DataFrame既有行索引也有列索引，它可以被看做由Series组成的字典。

    （3）数据理解

    3.1.查看数据结构

    1. #查看数据结构，即：几行几列
    2. data.shape

    1.2 机器学习——多元线性回归 - 图17
    说明：这是一个（200,5）的二维数据结构，即总共200行，每行有5列数据
    3.2.查看列名

    1. #查看数据列名称
    2. data.columns

    1.2 机器学习——多元线性回归 - 图18
    说明：此二维表结构的列名分别为Number、TV、radio、newspaper、sales
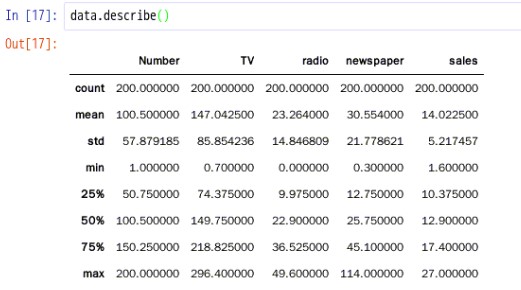
    3.3.查看描述统计

    1. #describe()函数对数据进行描述统计
    2. #describe()对每一列数据进行统计，包括计数，均值，std，最小值，最大值，各个分位数等
    3. data.describe()

    1.2 机器学习——多元线性回归 - 图19
    说明：

  • count计数：说明总共有200行，即200个记录；

  • mean均值：不同渠道广告费用的平均数；
  • std标准偏差：标准偏差(Std Dev,Standard Deviation) -统计学名词。一种度量数据分布的分散程度之标准，用以衡量数据值偏离算术平均值的程度。标准偏差越小，这些值偏离平均值就越少，反之亦然。
  • min、max最小值和最大值
  • 分位数（Quantile），也称分位点，是指将一个随机变量的概率分布范围分为几个等份的数值点，分析其数据变量的趋势

3.4.可视化特征与响应之间的关系

  1. #数据可视化，将数据以散点图的形式展现出来
  2. #导入可视化库matplotlib
  3. import matplotlib.pyplot as plt  
  4. %matplotlib inline  
  5. #seaborn也是一个可视化库
  6. import seaborn as sns  
  7. sns.pairplot(data, x_vars=['TV','radio','newspaper'], y_vars='sales', size=7, aspect=0.8, kind='reg') 
  8. plt.show()

1.2 机器学习——多元线性回归 - 图20
说明：seaborn的pairplot函数绘制X的每一维度和对应Y的散点图。通过设置size和aspect参数来调节显示的大小和比例。可以从图中看出，TV特征和销量是有比较强的线性关系的，而Radio和Sales线性关系弱一些，Newspaper和Sales线性关系更弱。通过加入一个参数kind=’reg’，seaborn可以添加一条最佳拟合直线和95%的置信带

（4）数据准备

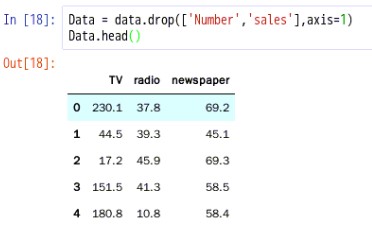
4.1.删除Number和sales这两列数据得到一个新的二维数组

  1. Data = data.drop(['Number','sales'],axis=1) 
  2. Data.head()

1.2 机器学习——多元线性回归 - 图21
4.2.获取原数据中的sales这一列数据

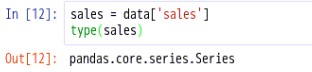
  1. sales = data['sales'] 
  2. type(sales)

1.2 机器学习——多元线性回归 - 图22
4.3.将多维的数组降为1维

  1. import numpy as np  
  2. sales = np.ravel(sales)  
  3. type(sales)

1.2 机器学习——多元线性回归 - 图23
4.4.构造训练集和测试集

  1. from sklearn.model_selection  import train_test_split  
  2. X_train, X_test, y_train, y_test = train_test_split(Data, sales, random_state=1)  
  3. # default split is 75% for training and 25% for testing
  4. print(X_train.shape) 
  5. print(y_train.shape) 
  6. print(X_test.shape) 
  7. print(y_test.shape)

1.2 机器学习——多元线性回归 - 图24
说明：将数据分为训练集和测试集，默认情况下，75%的数据用于训练，25%的数据用于测试

  • 训练集是用于发现和预测潜在关系的一组数据。训练集：Data数据为(200,3),X_train为(150,3),X_test为(50,3)

  • 测试集是用于评估预测关系强度和效率的一组数据。sales数据为200行，y_train为(150,)，y_test为（50,）

    （5）构建线性回归模型

    1. #Scikit-learn的线性回归
    2. #导入model
    3. from sklearn.linear_model import LinearRegression  
    4. #实例化线性回归
    5. linreg = LinearRegression()  
    6. #将模型拟合到训练数据
    7. linreg.fit(X_train, y_train)  
    8. #打印模型的系数
    9. print(linreg.intercept_) 
    10. print(linreg.coef_)

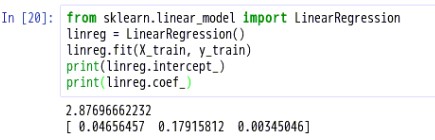
    1.2 机器学习——多元线性回归 - 图25
    说明：线性模型表达式： y=β0+β1x1+β2x2+…+βnxn 其中y是响应，β0是截距，β1是x1的系数，以此类推
    在这个案例中： y=β0+β1∗TV+β2∗radio+…+βn∗newspaper，β0的值为2.87696662232，β1的值为0.04656457，β2的值为0.17915812，β3的值为0.00345046
    如何解释各个特征对应的系数的意义？对于给定了Radio和Newspaper的广告投入，如果在TV广告上每多投入1个单位，对应销量将增加0.0466个单位

  • 对于给定了Radio和Newspaper的广告投入，如果在TV广告上每多投入1个单位，对应销量将增加0.0466个单位

  • 更明确一点，加入其它两个媒体投入固定，在TV广告上每增加1000美元（因为单位是1000美元），销量将增加46.6（因为单位是1000）

    （6）模型预测

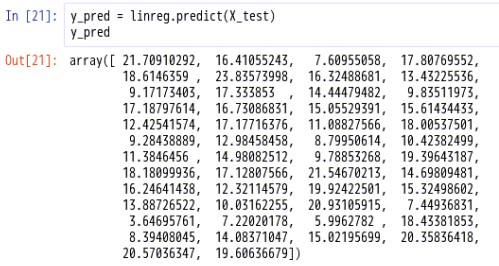
    对测试集进行预测
    1. #预测
    2. y_pred = linreg.predict(X_test)  
    3. y_pred
    1.2 机器学习——多元线性回归 - 图26

    （7）模型评价

    模型评估scikit-learn提供了包和方法
    包：sklearn.metrics
    sklearn.metrics包含评分方法、性能度量、成对度量和距离计算。

    7.1.将预测数据和测试数据绘制成图表形式

    1. #模型评价
    2. import matplotlib.pyplot as plt  
    3. plt.figure() 
    4. plt.plot(range(len(y_pred)),y_pred,'b',label='predict') 
    5. plt.plot(range(len(y_pred)),y_test,'r',label='test') 
    6. plt.legend(loc='upper right') 
    7. plt.xlabel('the number of sales') 
    8. plt.ylabel('value of sales') 
    9. plt.show()
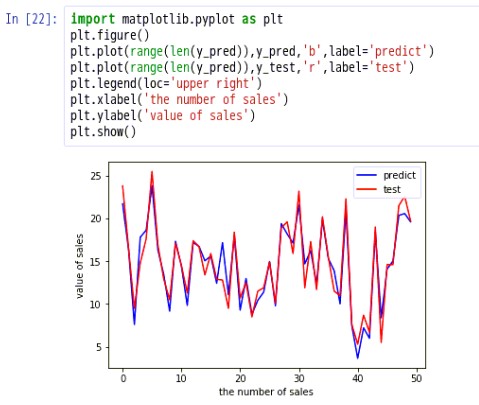
    1.2 机器学习——多元线性回归 - 图27
    说明：蓝色的表示predict预测，红色的表示test测试，观察发现，预测和测试线基本吻合，出入不是很大，如何用具体的数字表示呢？

    7.2.计算均方根误差RMSE来评估模型

    对于分类问题，评价测度是准确率，但这种方法不适用于回归问题。我们使用针对连续数值的评价测度(evaluation metrics)。下面介绍三种常用的针对回归问题的评价测度
    (1)平均绝对误差(Mean Absolute Error, MAE)，对应方法：metrics.mean_absolute_error(true, pred)
    (2)均方误差(Mean Squared Error, MSE)，对应方法：metrics.mean_squared_error(true, pred)
    (3)均方根误差(Root Mean Squared Error, RMSE)，对应方法：np.sqrt(metrics.mean_squared_error(true, pred))
    代码如下：
    1. from sklearn import metrics  
    2. import numpy as np  
    3. np.sqrt(metrics.mean_squared_error(y_test, y_pred))
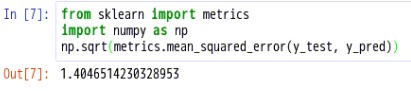
    1.2 机器学习——多元线性回归 - 图28
    RMSE的值为：1.4046514230328953，在之前展示的数据中，我们看到Newspaper和销量之间的线性关系比较弱，现在我们移除这个特征，看看线性回归预测的结果的RMSE如何？
    1. feature_cols = ['TV', 'radio'] 
    2. X = data[feature_cols]  
    3. y = data.sales  
    4. X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)  
    5. linreg.fit(X_train, y_train)  
    6. y_pred = linreg.predict(X_test)  
    7. np.sqrt(metrics.mean_squared_error(y_test, y_pred))
    1.2 机器学习——多元线性回归 - 图29
    我们将Newspaper这个特征移除之后，得到RMSE变小了，说明Newspaper特征不适合作为预测销量的特征，于是，我们得到了新的模型。我们还可以通过不同的特征组合得到新的模型，看看最终的误差是如何的。
    至此，实验结束！