1、图的基本表示

【数据结构与算法基础】代码仓库：https://github.com/jinrunheng/datastructure-and-algorithm

一：图的分类

什么是图，什么是图论？

图论（graph theory），是组合数学分支，和其他数学分支，如群论、矩阵论、拓扑学有着密切关系。图是图论的主要研究对象。图是由若干给定的顶点(Vertex)及连接两顶点的边(Edge)所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系。顶点用于代表事物，连接两顶点的边则用于表示两个事物间具有这种关系。

图论起源于著名的柯尼斯堡七桥问题。该问题于1736年被欧拉解决，因此普遍认为欧拉是图论的创始人。

图的分类

图可以分为四类：

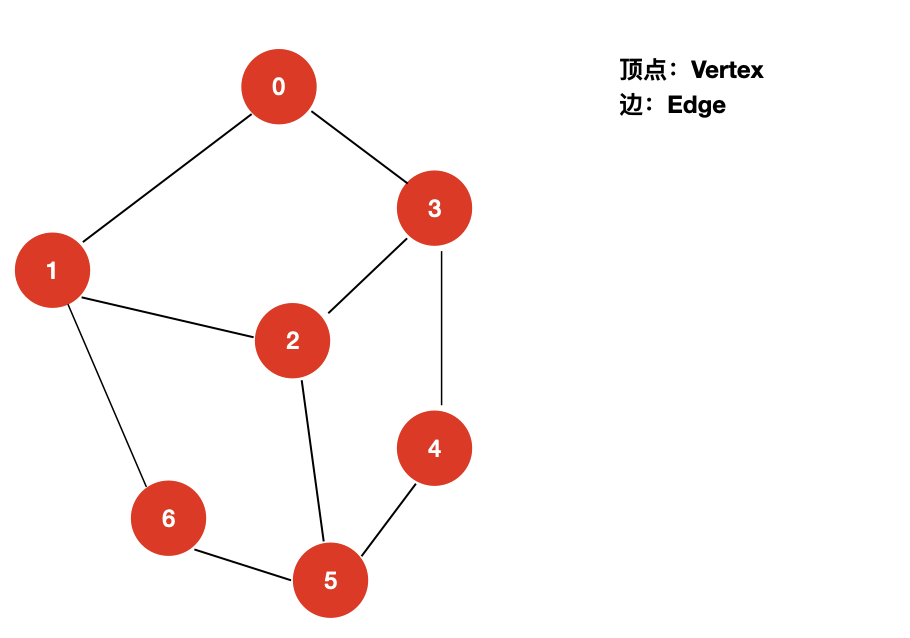
• 无向无权图

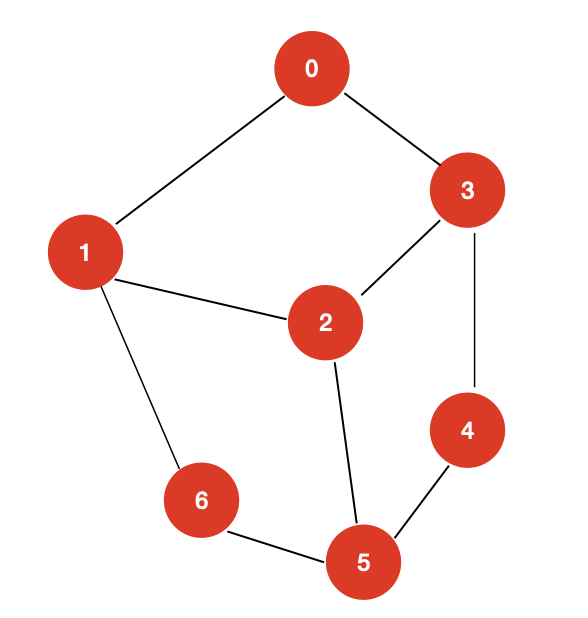
• 有向无权图

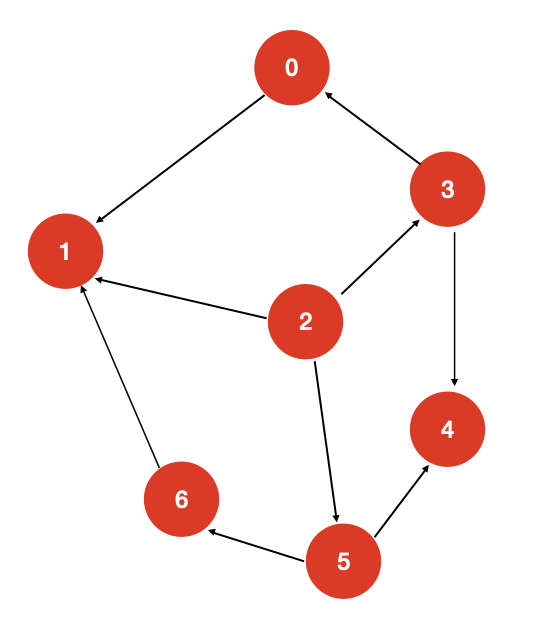
• 无向有权图

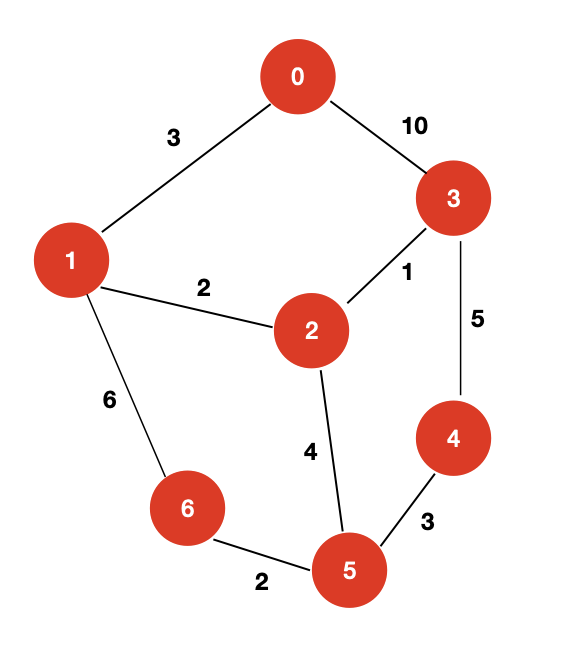
• 有向有权图

二：图的基本概念

1. 有向完全图

有向完全图是指，有向图中有 n 个顶点，有 n(n - 1) 条边，即：图中的每个顶点和其余 n - 1 个顶点都相连

1. 无向完全图

无向完全图是指，无向图中有 n 个顶点，有 n(n - 1)/2 条边，即：图中的每个顶点和其余 n - 1 个顶点都相连

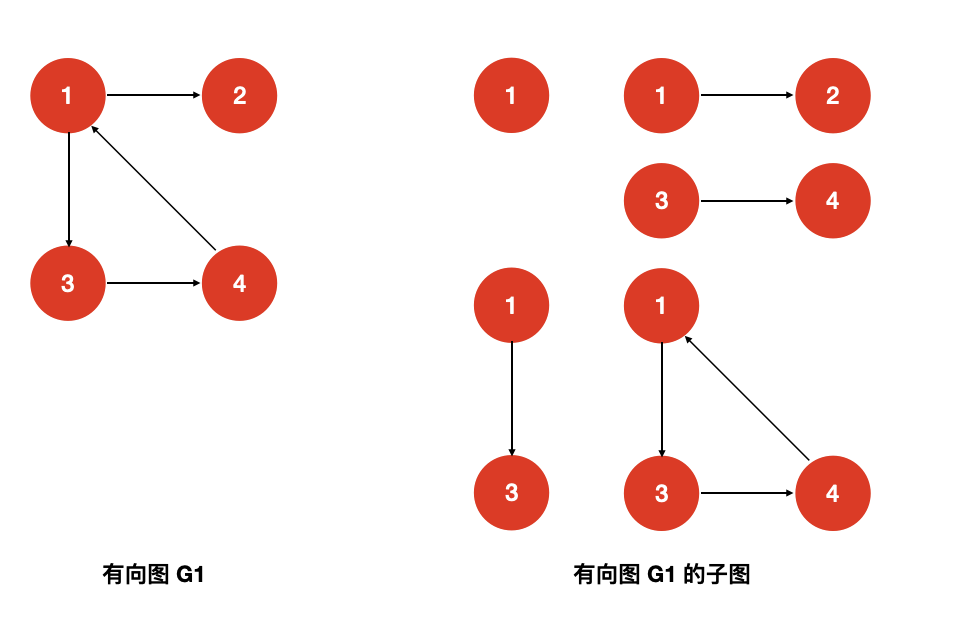
1. 子图

设有两个图G = (V,{E})和G' = (V',{E'})，若满足 且 ，则称图 G' 为 G的子图
示例：

1. 邻接点

如果顶点 v 和 顶点 w 存在一条边，则称顶点 v 和顶点 w 互为邻接点

1. 路径和环

   • 路径：从顶点 v 到 顶点 w 的连续线段序列
   • 路径长度：顶点序列上经过的边的个数
   • 环：路径起点和路径终点相同

2. 自环边和平行边

   • 自环边：若一条边的两个顶点相同（即顶点自己指向自己），就将该边称为自环边
   • 平行边：平行边是指从一个顶点连接到另一个顶点的多余边

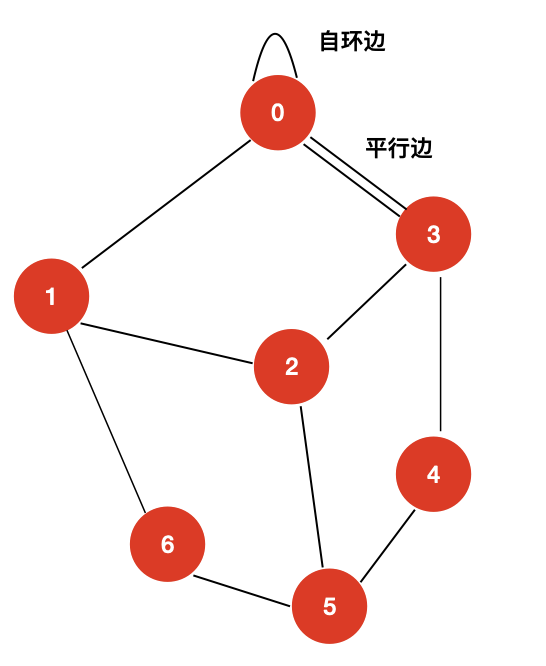
1. 简单图

简单图是指不含自环边和平行边的图

1. 联通图与联通分量

对于图中的两个顶点 v 和 w，有路径，则称 v 和 w 联通。如果图中任意两个顶点都是联通的，则称该图为联通图。那么什么是联通分量呢？联通分量是指无向图中的极大联通子图。

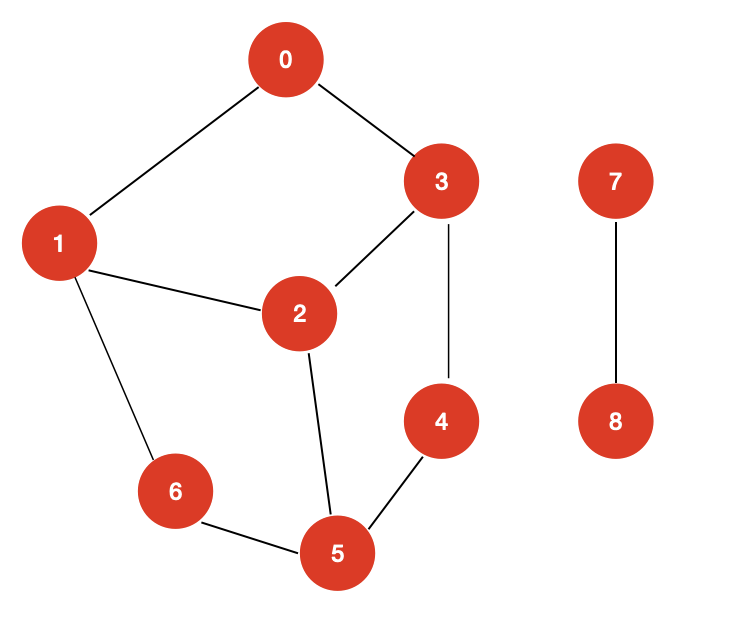
对于上面的图中，存在两个联通分量。

1. 度

对于无向图，顶点 v 的度是指和顶点 v 相连的边的个数。

对于有向图，顶点 v 的度分为出度和入度两部分；顶点 v 被箭头指向的个数就是它的入度，从顶点 v 指出去的箭头个数就是它的出度。

1. 生成树

树是一种特殊的图，当一棵树包含联通图的所有顶点，且这棵树的边为该图的边的子集时，我们就称该树是这个联通图的生成树。

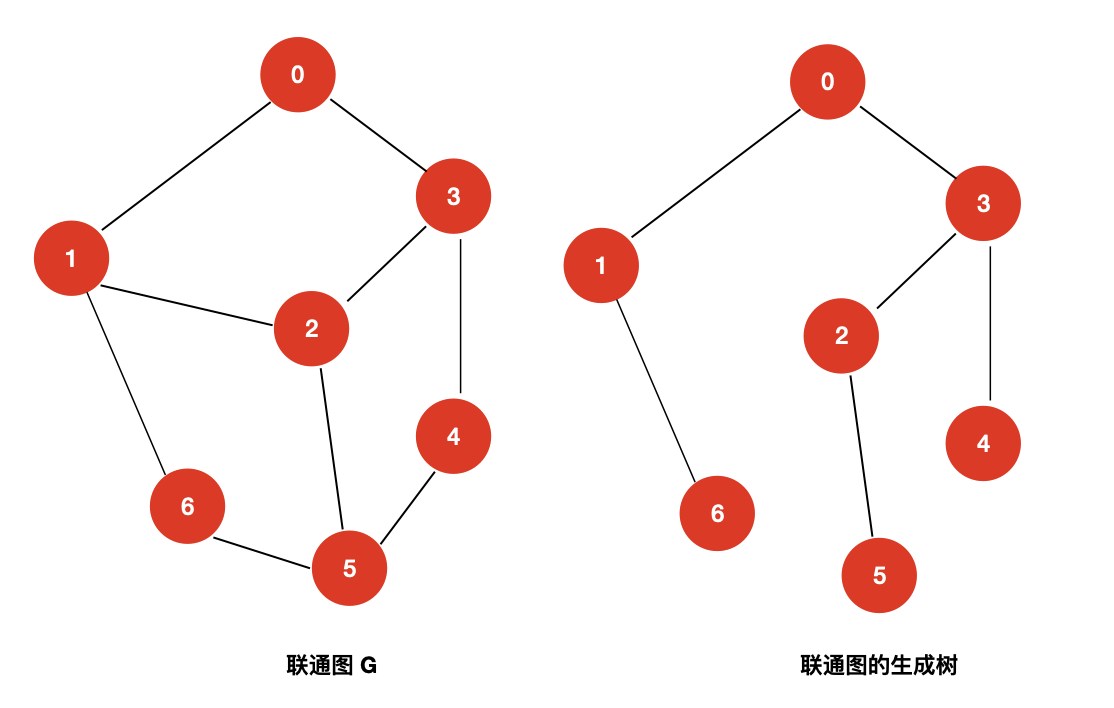
假设联通图有 n 个顶点，那么，联通图的生成树的边的个数为 n - 1 个。

三：图的基本表示之邻接矩阵

代码链接🔗

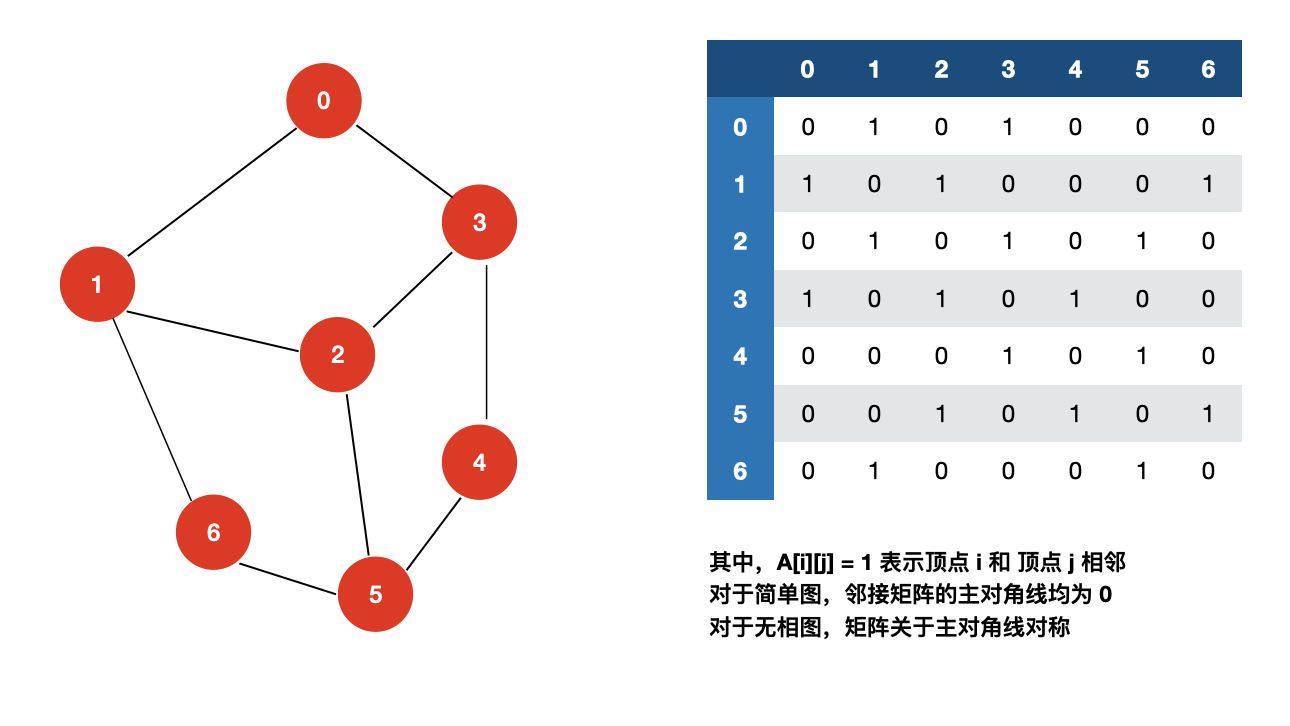
图的信息是如何给定的呢？

对于上面的示例，我们给定关于图的信息如下：

7 9
0 1
0 3
1 2
1 6
2 3
2 5
3 4
4 5
5 6

第一行，7 代表图有 7 个顶点，9 代表图中有 9 条边；第一行后面每一行的信息均表示顶点 v 和顶点 w 相邻。

对于邻接矩阵，我们设计的方法主要有以下几个：

• 建图
• 查看两点是否相邻
• 求一个顶点的相邻顶点

建图我们需要遍历给定的图的基本信息，也就是遍历图的所有边，这个时间复杂度为 O(E)；查看两点是否相邻这个方法我们只需要去对应的矩阵中直接查看信息即可，时间复杂度为 O(1)。

而求一个顶点的相邻节点，我们需要遍历所有的顶点，这个时间复杂度为 O(V)

public List<Integer> adj(int v) {
    validateVertex(v);
    List<Integer> res = new ArrayList<>();
    for (int i = 0; i < V; i++) {
        if (adj[v][i] == 1) {
            res.add(i);
        }
    }
    return res;
}
private void validateVertex(int v) {
    if (v < 0 || v >= V)
        throw new IllegalArgumentException("vertex" + v + "is invalid");
}

并且，我们存储图使用的空间为 V2 , 空间复杂度为 O(V2) 。

四：图的基本表示之邻接表

代码链接🔗

使用邻接矩阵表示图出现的最大问题在于建图的空间复杂度和求一个顶点的相邻节点的算法。

试想一下，如果一个图是稀疏图，假设图中包含 3000 个节点，仅仅有 10 条边，我们就需要使用 30002的空间去存储及表示图，并且求解一个顶点的相邻节点的算法也需要遍历所有的顶点，毫无疑问，这是低效的。

我们通过举例分析了邻接矩阵这种图的表示方法带来的问题，对于边的数量相对于顶点数量很少的稀疏图，邻接矩阵会极大浪费存储空间。

除了邻接矩阵这种表示方法之外，图还有另外一种表示方法：邻接表。

邻接表对每一个顶点都使用一个链表存储，每个链表存储与该顶点相邻的顶点

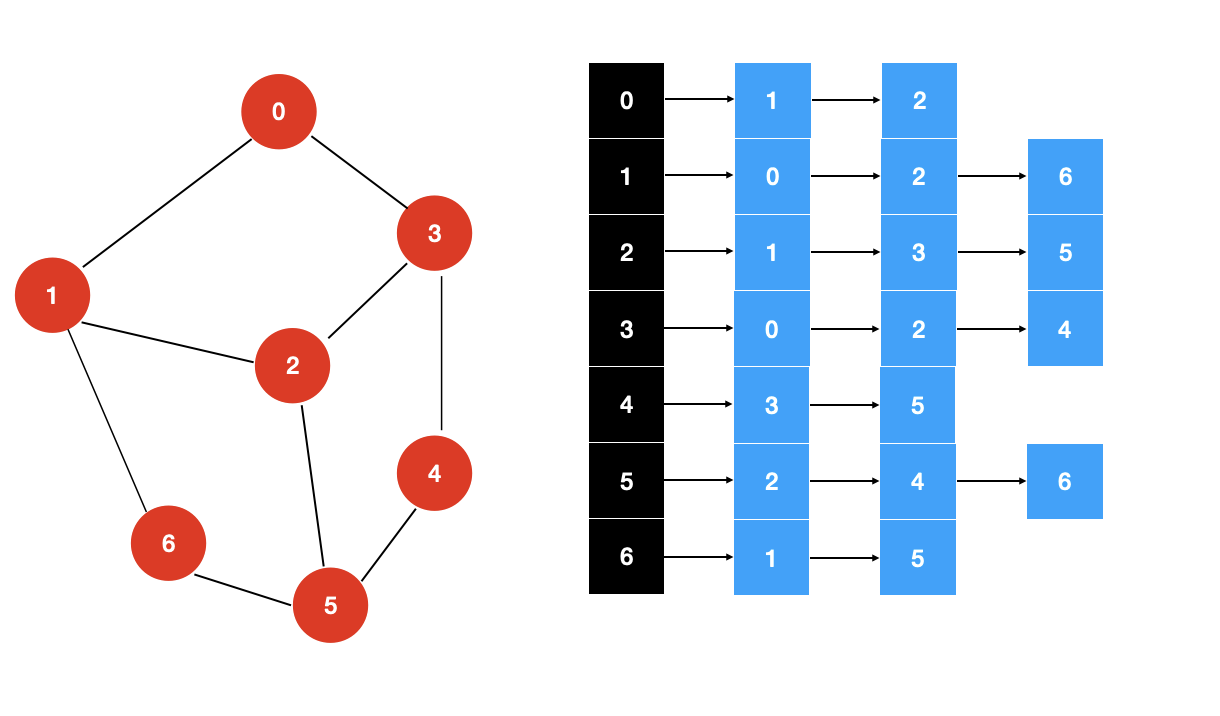
邻接表的复杂度分析：

空间复杂度：O(V + E)

使用邻接表，有多少个顶点，就需要使用多少个链表，每个链表存储相邻节点，在简单图中（不考虑平行边和自环边），每个边计算了两次，所以邻接表存储的空间复杂度为 O(V + 2E)，省略掉常数项，空间复杂度为 O(V + E)。

时间复杂度分析：

• 建图：O(E * V)，因为对于每一次遍历，我们都需要查看是否有平行边，最差的情况为完全图，那么，链表的查询操作为 O(V)
• 查看两点是否相邻：O(degree(v)) ，其中 degree(v) 为 v 这个顶点的度，最差的情况为完全图，该操作的时间复杂度为 O(V)
• 求一个顶点的相邻节点：O(degree(v)) ，其中 degree(v) 为 v 这个顶点的度，最差的情况为完全图，该操作的时间复杂度为 O(V)

五：邻接表的改进

代码链接🔗

通过上面对邻接表的分析，我们发现查看两个顶点是否相邻的复杂度为 O(degree(v))，并且建图时，我们都要执行一个查重操作，其原因在于我们的存储结构为线性的链表，如果我们将存储结构改进为红黑树（TreeSet）或者是哈希表（HashSet），就可以更进一步地提升查找算法的时间复杂度。其实无论红黑树还是哈希表，这两种数据结构的时间复杂度差异也并不会很大，这里我将使用红黑树这种数据结构。

六：图的基本表示的比较

代码链接🔗

由我们的分析可知，使用邻接表（TreeSet）用来表示图是一种相对较优的选择。