【数据结构与算法基础】代码仓库：https://github.com/jinrunheng/datastructure-and-algorithm

一：算法笔试面试中图论问题的书写

我们以 LeetCode 上面的一个问题 785. 判断二分图 来具体看一下算法笔试面试中，图论问题的书写：

和我们之前编写的算法类不同，像算法面试和笔试中，关于图论问题一般会直接给出图的定义，所以，这里面不需要我们去自己去对图进行建模。像 LeetCode 785 号问题中，给定的输出是一个二维数组 graph，其中 graph[v] 是一个节点数组，表示节点 v 的邻接节点。对于一个无向图，判断是否是二分图的技巧，我们已经在 DFS 和 BFS 的章节中给出了详细的解释，主要就是在 DFS 或 BFS 的过程中进行染色操作。在这里就我就不做多余的说明了，直接给出 DFS 和 BFS 的详细的代码：

DFS

  1. class Solution {
  3.     private int[][] graph;
  4.     private boolean[] visited;
  5.     private int[] colors;
  7.     public boolean isBipartite(int[][] graph) {
  8.         this.graph = graph;
  9.         visited = new boolean[graph.length];
  10.         colors = new int[graph.length];
  11.         for(int i = 0; i < graph.length; i++)
  12.             colors[i] = -1;
  14.         for(int v = 0; v < graph.length; v++)
  15.             if(!visited[v])
  16.                 if(!dfs(v,0))
  17.                     return false;
  19.         return true;
  20.     }
  22.     private boolean dfs(int v,int color){
  23.         visited[v] = true;
  24.         colors[v] = color;
  26.         for(int w : graph[v])
  27.             if(!visited[w]){
  28.                 if(!dfs(w,1 - color))
  29.                     return false;
  30.             }else if(colors[w] == colors[v]){
  31.                 return false;
  32.             }
  34.         return true;
  35.     }
  36. }

BFS

  1. class Solution {
  3.     private int[][] graph;
  4.     private boolean[] visited;
  5.     private int[] colors;
  7.     public boolean isBipartite(int[][] graph) {
  8.         this.graph = graph;
  9.         this.visited = new boolean[graph.length];
  10.         this.colors = new int[graph.length];
  11.         for(int i = 0; i < colors.length; i++)
  12.             colors[i] = -1;
  14.         for(int v = 0; v < graph.length; v++)
  15.             if(!visited[v])
  16.                 if(!bfs(v))
  17.                     return false;
  19.         return true;
  20.     }
  22.     private boolean bfs(int v){
  23.         Queue<Integer> q = new LinkedList<>();
  24.         visited[v] = true;
  25.         colors[v] = 0;
  26.         q.offer(v);
  28.         while(!q.isEmpty()){
  29.             v = q.poll();
  31.             for(int w : graph[v])
  32.                 if(!visited[w]){
  33.                     visited[w] = true;
  34.                     colors[w] = 1 - colors[v];
  35.                     q.offer(w);
  36.                 }else if(colors[w] == colors[v]){
  37.                     return false;
  38.                 }   
  40.         }
  41.         return true;
  42.     }
  43. }

二：图的建模

我们继续以 LeetCode 中的问题来学习如何对一个图论问题进行图的建模。

这一次，我们来看 LeetCode 第 695 号问题：695. 岛屿的最大面积。

对于这个问题，题目给定的输入 grid 是一个二维数组：

  1. [[0,0,1,0,0,0,0,1,0,0,0,0,0],
  2.  [0,0,0,0,0,0,0,1,1,1,0,0,0],
  3.  [0,1,1,0,1,0,0,0,0,0,0,0,0],
  4.  [0,1,0,0,1,1,0,0,1,0,1,0,0],
  5.  [0,1,0,0,1,1,0,0,1,1,1,0,0],
  6.  [0,0,0,0,0,0,0,0,0,0,1,0,0],
  7.  [0,0,0,0,0,0,0,1,1,1,0,0,0],
  8.  [0,0,0,0,0,0,0,1,1,0,0,0,0]]

我们可以将其看作是一个图：
image.png

二维数组中的每一个元素作为一个顶点，如果一个顶点的值为 1，则表示该顶点是一块陆地，如果该顶点上下左右四个方向有一块是陆地，则陆地与陆地之间就会形成一条边。

题目要求我们返回岛屿最大的面积，实际上就是求解联通分量这个问题，只不过题目要求我们返回的结果是最大联通分量中的顶点个数是多少。

对于题目给定的二维数组 grid，我们需要将其转换为一维数组的图的顶点的表示方式，二者的关系式如下：

// grid[x][y]
// C 表示二维数组有多少列
int v = x * C + y;

x = v / C;
y = v % C;

将 grid 数组转换为图的表示方式，对图进行建模后，这个问题也就迎刃而解了。

代码如下：

class Solution {

    private int r,c;
    private HashSet<Integer>[] G;
    private int[][] dirs = {{-1,0},{0,1},{1,0},{0,-1}};
    private boolean[] visited;

    public int maxAreaOfIsland(int[][] grid) {
        if(grid == null || grid.length == 0 || grid[0] == null || grid[0].length == 0)
            return 0;

        r = grid.length;        
        c = grid[0].length;
        G = constructGraph(grid);
        visited = new boolean[G.length];

        int res = 0;
        for(int v = 0; v < G.length; v++) {
            int x = v / c;
            int y = v % c;
            if(!visited[v] && grid[x][y] == 1){
                res = Math.max(res,dfs(v));
            }
        }


        return res;    
    }

    /**
     * 有语意的 dfs ，返回一个联通分量的顶点的个数
     */
    private int dfs(int v){
        visited[v] = true;

        int res = 1;
        for(int w : G[v])
            if(!visited[w]){
                res += dfs(w);
            }
        return res;
    }

    private HashSet<Integer>[] constructGraph(int[][] grid){
        HashSet<Integer>[] g = new HashSet[r * c];
        for(int i = 0; i < g.length; i++)
            g[i] = new HashSet<>();

        for(int v = 0; v < g.length; v++){
            int x = v / c;
            int y = v % c;
            if(grid[x][y] == 1){
                for(int d = 0; d < 4; d++){
                    int nextX = x + dirs[d][0];
                    int nextY = y + dirs[d][1];
                    if(isValid(nextX,nextY) && grid[nextX][nextY] == 1){
                        int next = nextX * c + nextY;
                        g[v].add(next);
                        g[next].add(v);
                    }
                }
            }
        }   
        return g; 
    }

    private boolean isValid(int x,int y){
        return x >= 0 && x < r && y >= 0 && y < c;
    }
}

三：Flood Fill 算法

在上一小节中，对于 LeetCode 第 695 号问题：岛屿的最大面积，我们首先是通过题目给定的条件进行图的建模，然后使用图论算法的 DFS 遍历解决了该问题。

但是，我们仔细思考，题目给定的二维数组 grid 本质上就是一个图，有没有方法可以不建图，直接在 grid 上进行 DFS 操作呢？

其实，这是完全可行的，我们之前使用的 visited 数组是一个一维数组，用来记录每个顶点是否被遍历过；我们换一种思想，如果直接在 grid 上进行 DFS 遍历，那么相应的，就要建立一个二维数组 visited， 其大小和 grid 保持一致，用这个二维数组 visited 表示每一个点是否被遍历过。

代码改进如下：

class Solution {

    int r,c;
    private boolean[][] visited;
    private int[][] grid;
    private int[][] dirs = {{-1,0},{0,1},{1,0},{0,-1}};

    public int maxAreaOfIsland(int[][] grid) {
        if(grid == null || grid.length == 0 || grid[0] == null || grid[0].length == 0)
            return 0;

        r  = grid.length;
        c = grid[0].length;    
        this.grid = grid;
        visited = new boolean[r][c];

        int res = 0;
        for(int x = 0; x < r; x++)
            for(int y = 0; y < c; y++)
                if(grid[x][y] == 1)
                    res = Math.max(res,dfs(x,y));

        return res;
    }

    private int dfs(int x,int y){
        visited[x][y] = true;

        int res = 1;
        for(int d = 0; d < 4; d++){
            int nextX = x + dirs[d][0];
            int nextY = y + dirs[d][1];
            if(isValid(nextX,nextY) && !visited[nextX][nextY] && grid[nextX][nextY] == 1)
                res += dfs(nextX,nextY);
        }
        return res;
    }
    private boolean isValid(int x,int y){
        return x >= 0 && x < r && y >= 0 && y < c;
    }
}

和上一小节不同的是，我们将题目给定的二维数组 grid 直接想成了一个图，并且在 grid 这张“图”上进行了 DFS 遍历。

这个算法有一个名字叫做：Flood Fill。

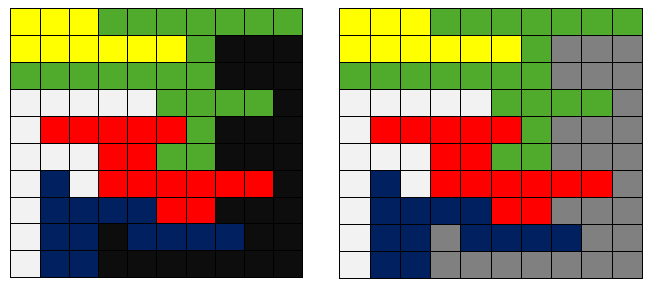
image.png

Flood Fill 算法是从一个区域中提取若干个联通的点与其他相邻区域区分开（或类似于染色）的经典算法。因为其思路类似于洪水从一个区域扩散到所有能到达的区域而得名。

Flood Fill 算法的应用也是非常广泛的，譬如扫雷游戏：

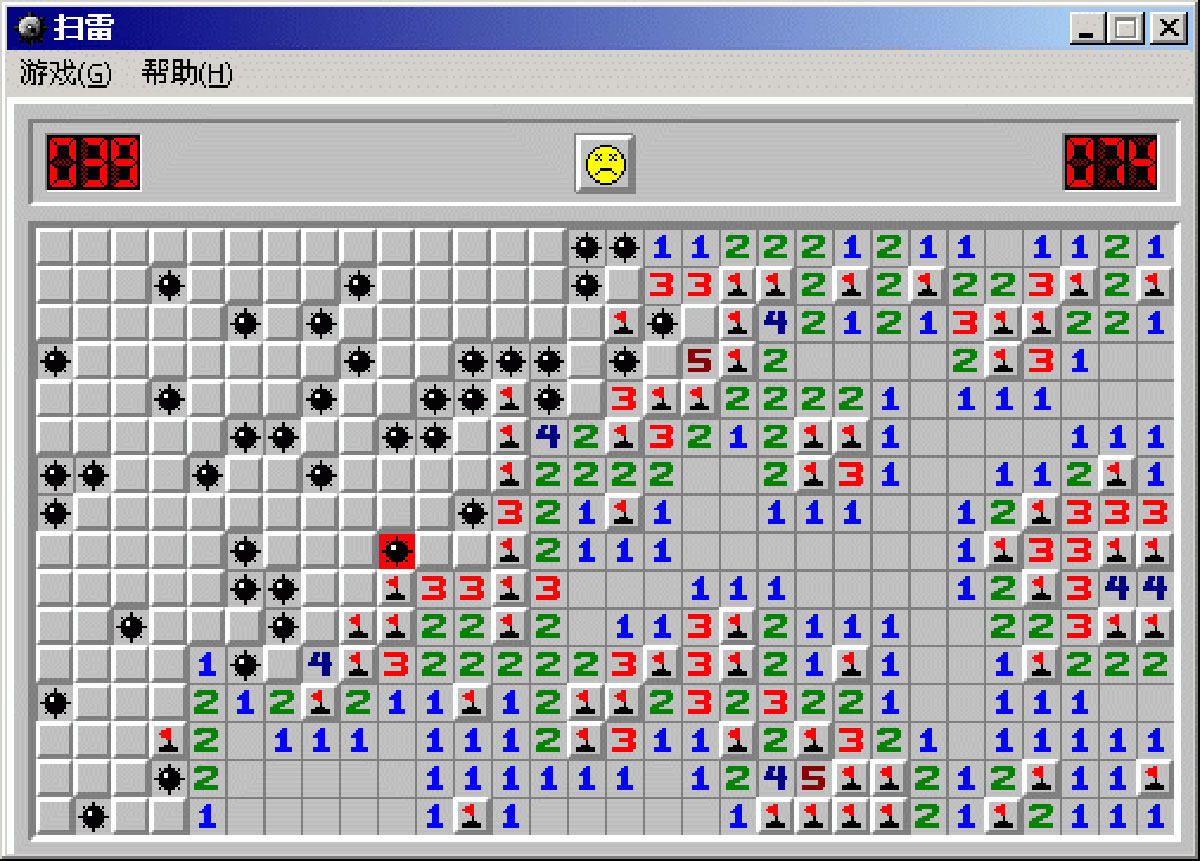
image.png

如果我们点击一个点，它周围的八个格子都没有雷的话就会展开一片区域，展开这片区域就是使用了 Flood Fill 算法。

又譬如消除游戏：

image.png

如果我们点击一个图案，和这个点连接的区域如果是相同的图案时，就会消除，这个消除的实现也是 Flood Fill 算法。

说了这么多，其实，聪明如你肯定也意识到了，Flood Fill 的本质还是图的遍历。

四：更多关于 Flood Fill 算法的问题

LeetCode 上更多关于 Flood Fill 算法的相关问题如下，大家如果有兴趣可以自己尝试，也可以关注我的代码仓库，在我的代码仓中也有关于这些问题的题解～