2、图的深度优先遍历

【数据结构与算法基础】代码仓库：https://github.com/jinrunheng/datastructure-and-algorithm

一：数据结构遍历的意义

图是一种数据结构，每种数据结构，都必须有“遍历”的方式，很多算法，本质都是遍历。

对于线性数据结构

遍历是从头到尾访问线性结构的每个元素。

对于一棵二叉树，也存在着多种遍历方式，按照访问树的节点的顺序可以分为：前序，中序，后序遍历以及层序遍历。前序，中序，后序遍历都是一种深度优先遍历，按层遍历是一种广度优先遍历。

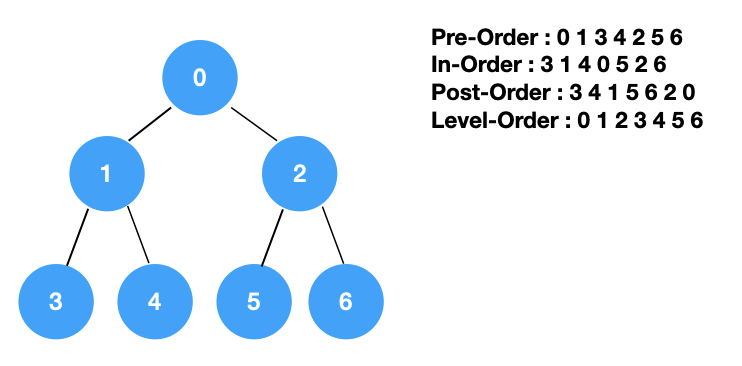
图的遍历整体也可以分为两大类：深度优先遍历与广度优先遍历。

那么图的遍历和树的遍历有什么本质的不同呢？

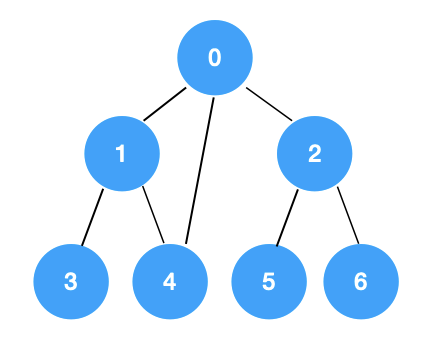
假设我的图结构如上图所示，如果我使用树的深度优先遍历方式来遍历我们的图，我们就会发现，图是具有环状结构的，会产生重复遍历的情况。在对图遍历的时候，我们需要记录，哪个节点被遍历过了。

二：从树的深度优先遍历到图的深度优先遍历

树的深度优先遍历

拿前序遍历来说，树的优先遍历伪码如下：

perirder(root);
preorder(TreeNode node){
    if(node != null) {
        list.add(node.val);
        preorder(node.left);
        preorder(node.right);
    }
}

图的深度优先遍历

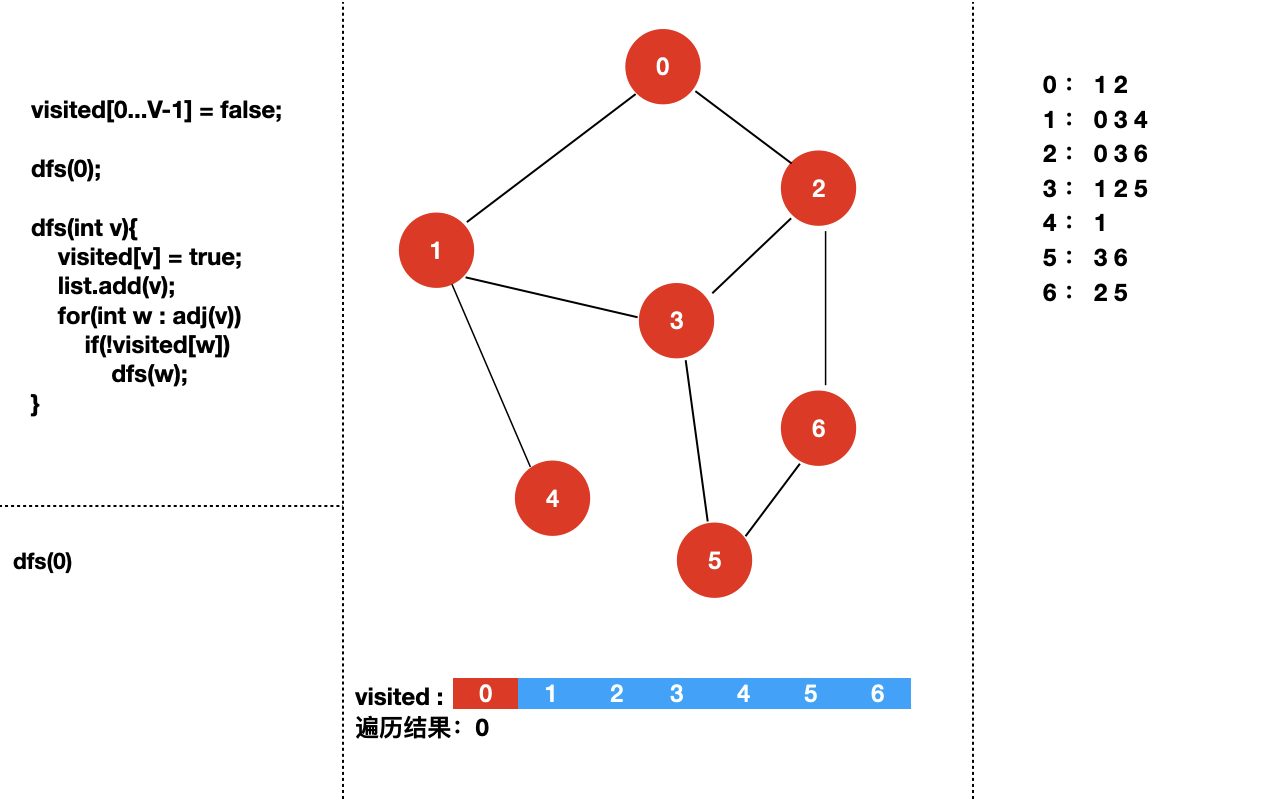
图的深度优先遍历伪码如下，我们会声明一个数组，记录哪个节点已经被遍历过，在逻辑上与树的深度优先遍历其实并没有本质上的不同，只是我们访问了一个节点，就要在声明的数组中，将访问的节点标记为已访问的状态。

visited[0...V-1] = false;
dfs(0);
dfs(int v){
    visited[v] = true;
    list.add(v);
    for(int w : adj(v))
        if(!visited[w])
            dfs(w);
}

三：DFS 逻辑的微观解读

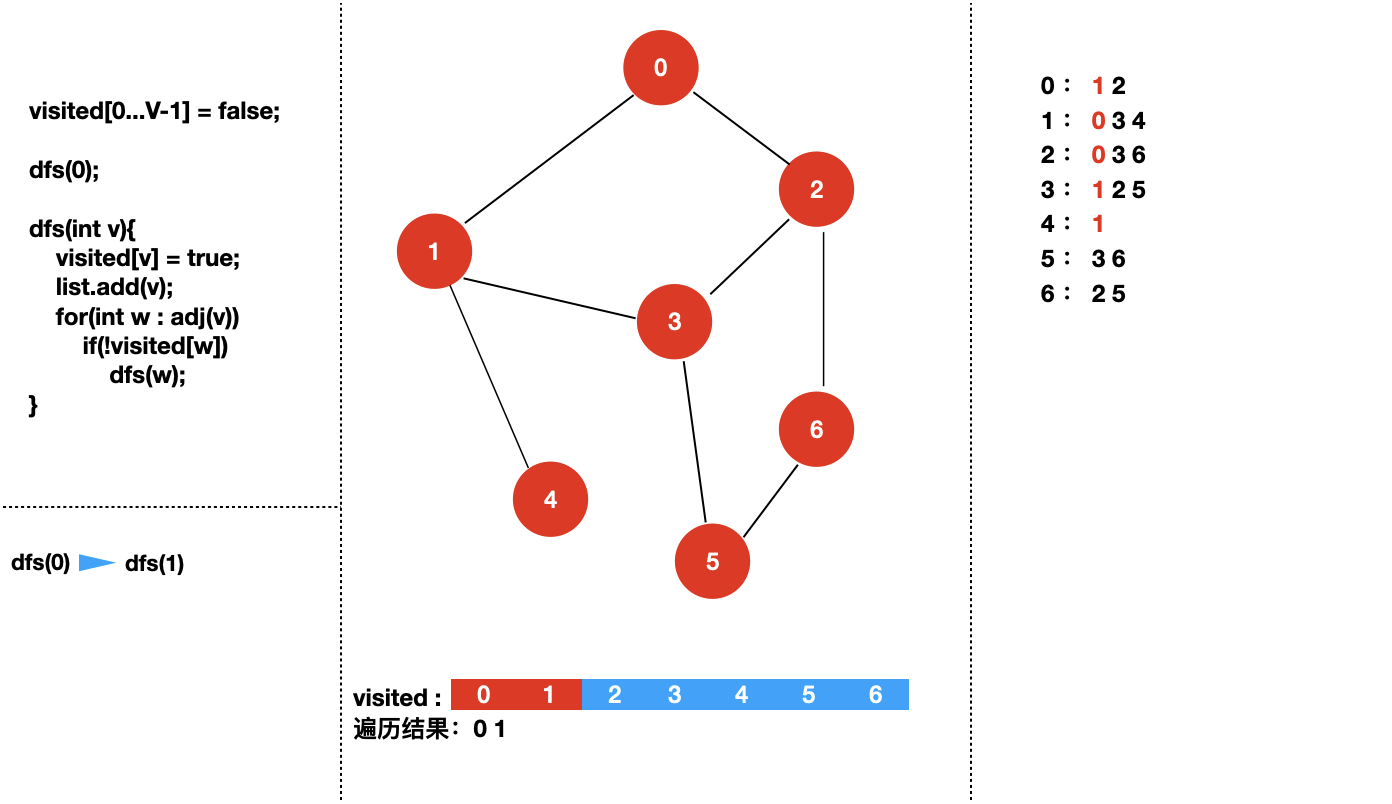
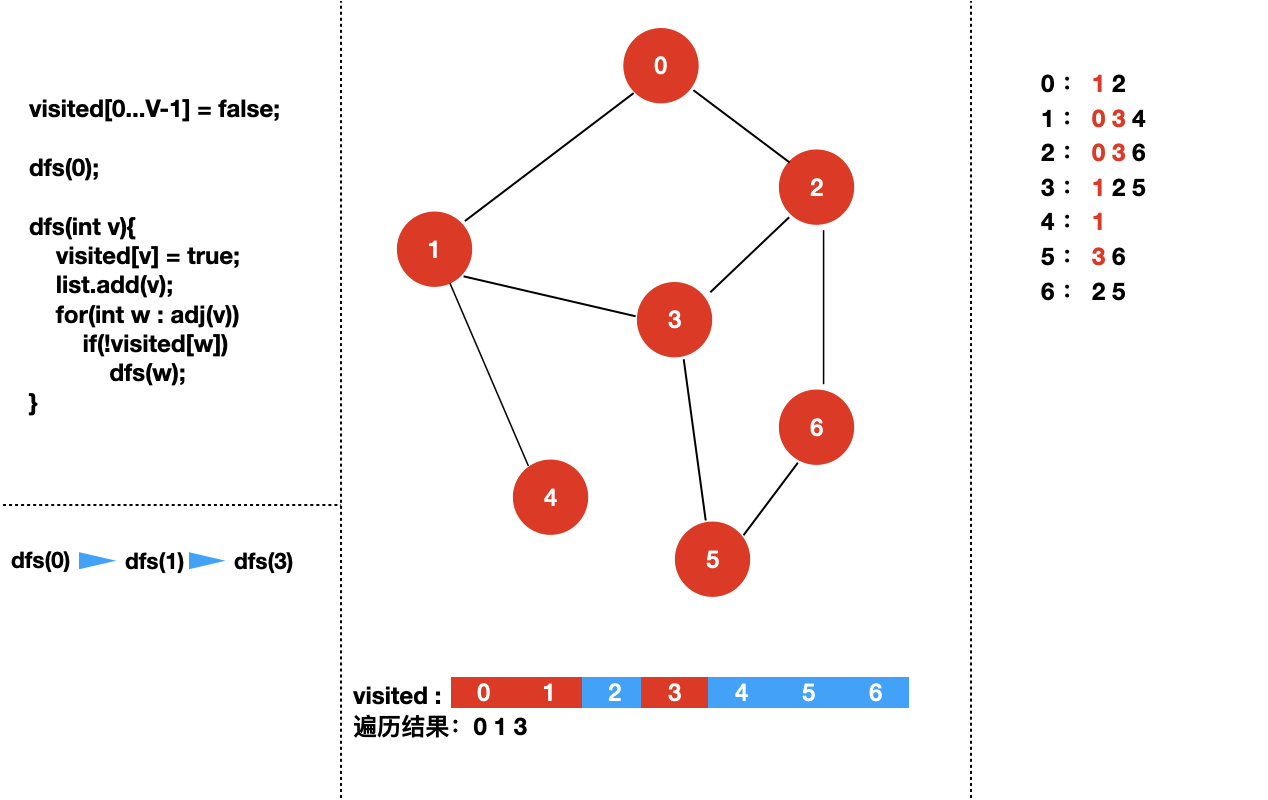
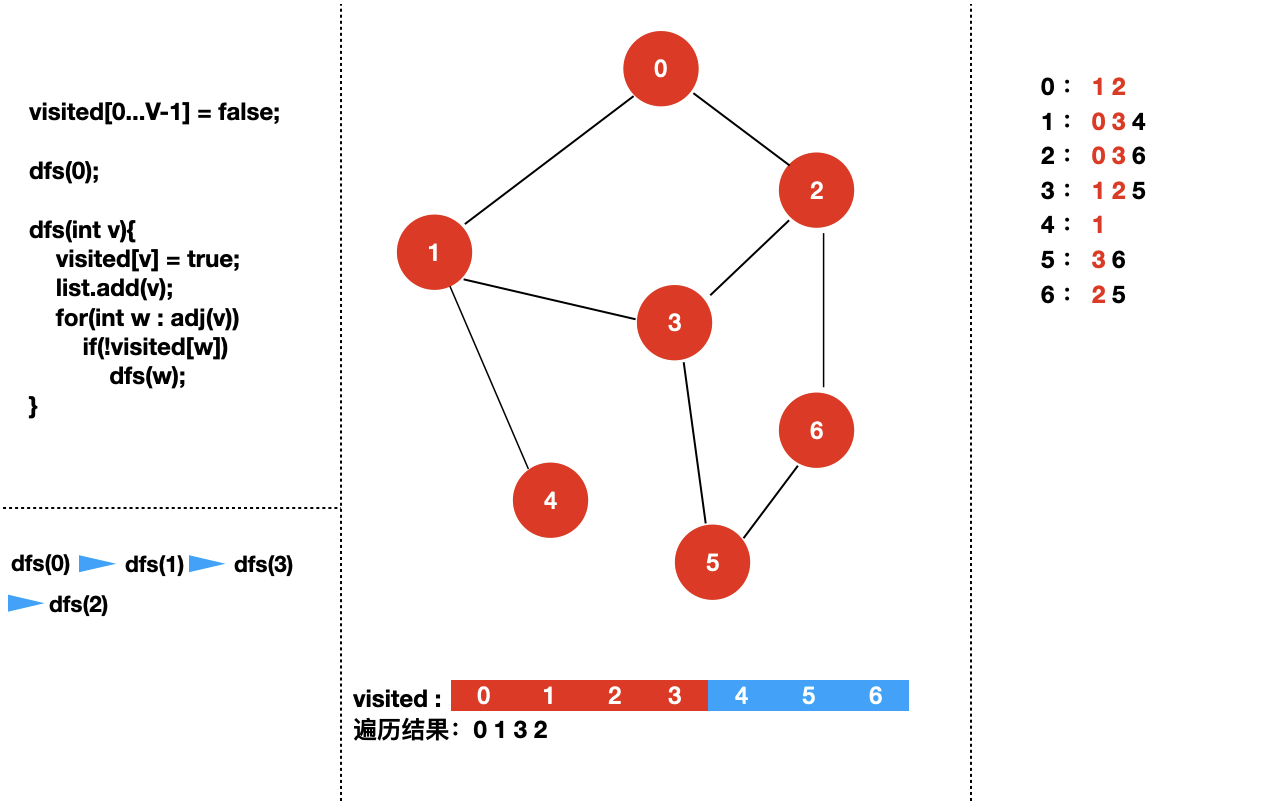
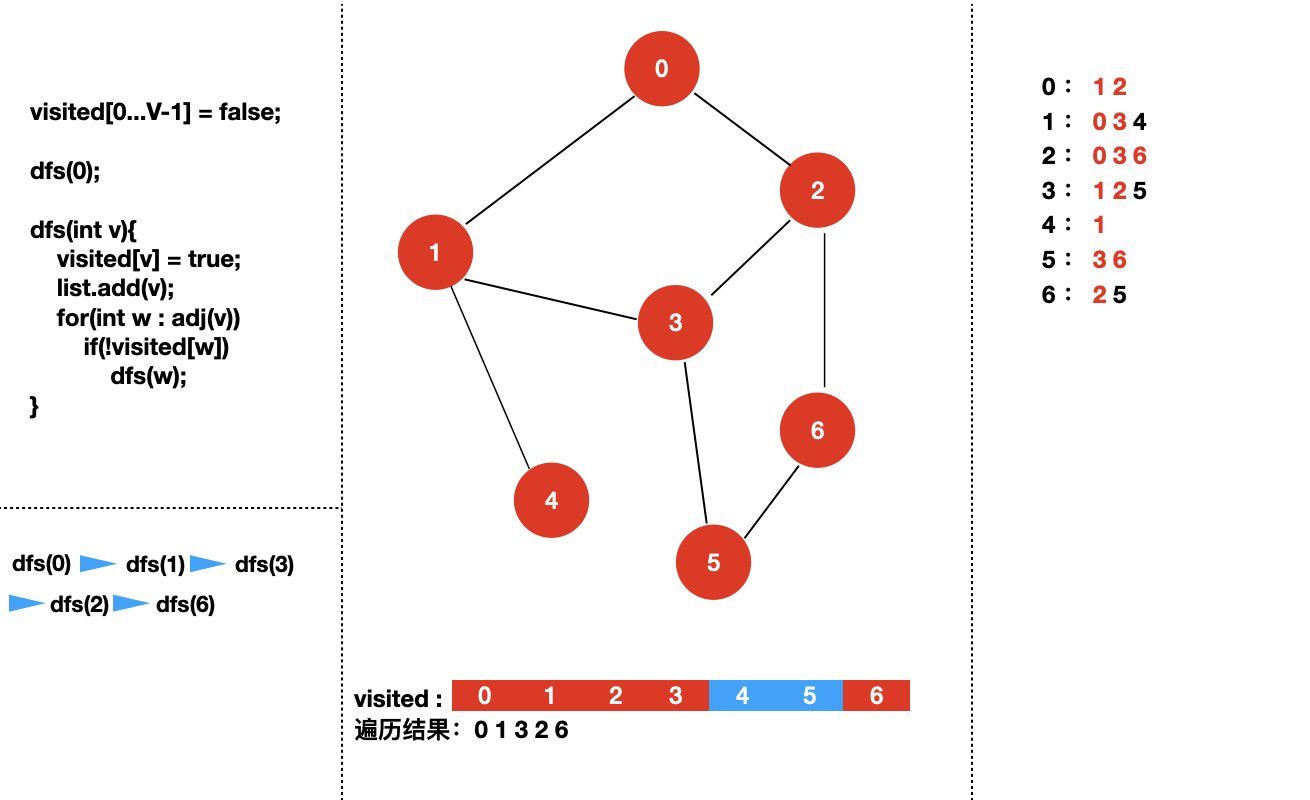
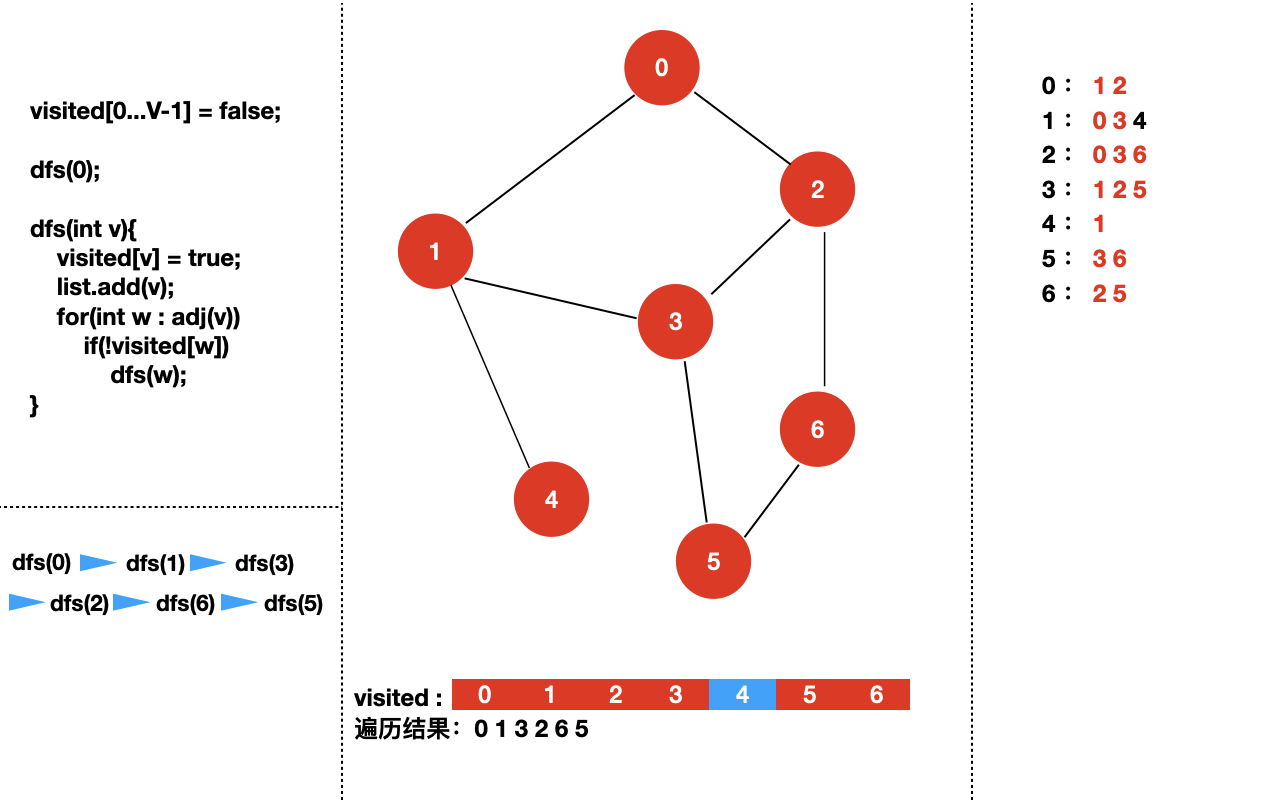
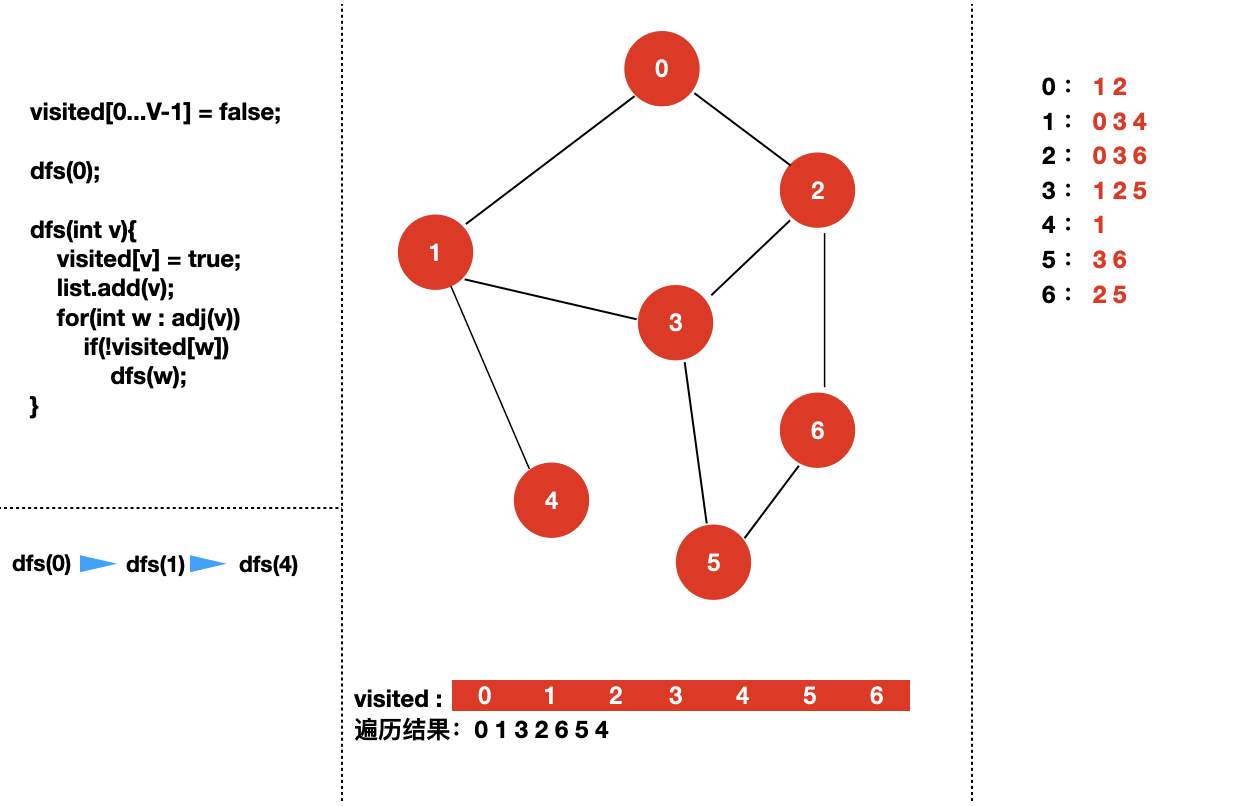
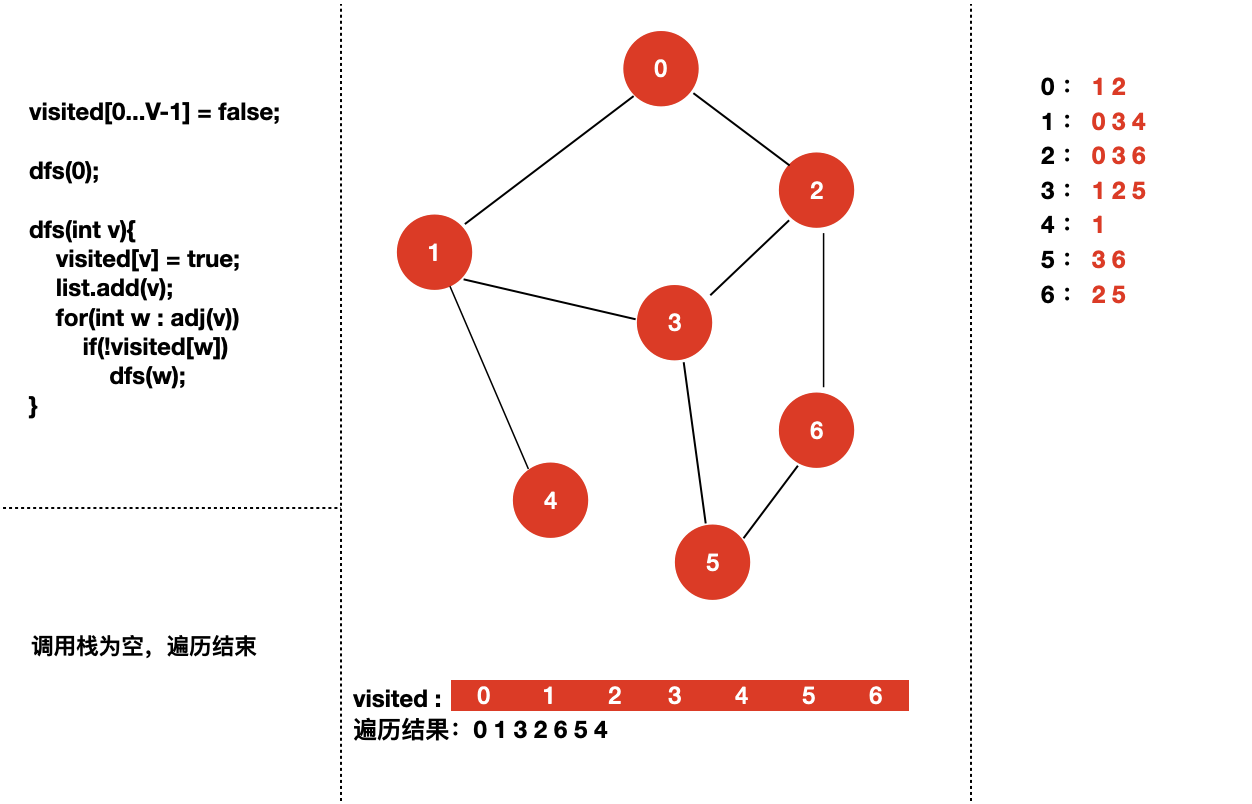
接下来，我们来具体看一下对于下面个图，深度优先遍历的过程是怎样的？

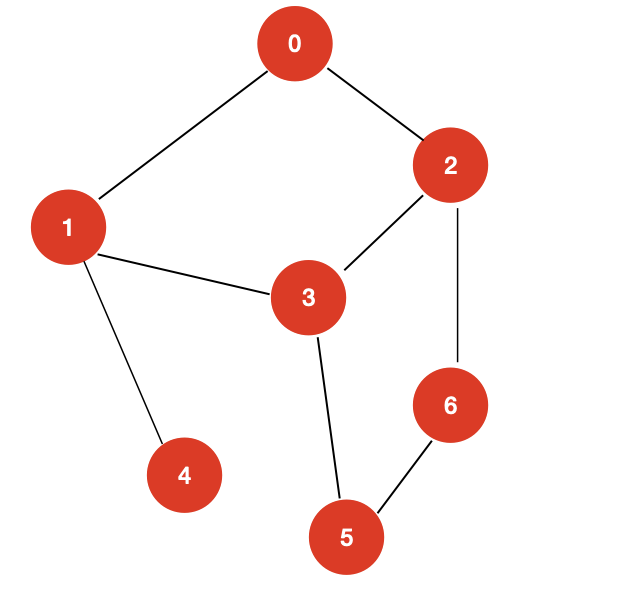
我们从 dfs(0) 开始。

四：实现图的深度优先遍历

代码链接🔗

代码如下：

visited[0...V] = false;
for(int v = 0; v < V; v++)
    if(!visited[v])
        dfs(v);
dfs(int v) {
    visited[v] = true;
    list.add(v);
    for(int w : adj(v))
        if(!visited[w])
            dfs(w);
}

这是深度优先遍历的前序遍历方式，同理，也有深度优先遍历的后续遍历方式：

visited[0...V] = false;
for(int v = 0; v < V; v++)
    if(!visited[v])
        dfs(v);
dfs(int v) {
    visited[v] = true;
    for(int w : adj(v))
        if(!visited[w])
            dfs(w);
    list.add(v);
}

五：更多关于图的深度优先遍历

图的深度优先遍历的应用

• 求图的联通分量
• 求两点间是否可达
• 求两点间的一条路径
• 检测图中是否有环
• 二分图检测
• 寻找图中的桥
• 寻找图中的割点
• 哈密尔顿路径
• 拓扑排序
• … …

非递归方式实现图的深度优先遍历

代码链接🔗

非递归方式实现图的深度优先遍历代码如下：

visited[0...V] = false;
for(int v = 0; v < V; v++)
    if(!visited[v])
        dfs(v);
dfs(int v) {
    Stack<Integer> stack = new Stack<>();
    stack.push(v);
    visited[v] = true;
    while (!stack.isEmpty()) {
        int cur = stack.pop();
        list.add(cur);
        for (int w : G.adj(cur)) {
            if (!visited[w]) {
                stack.push(w);
                visited[w] = true;
            }
        }
    }
}