【数据结构与算法基础】代码仓库：https://github.com/jinrunheng/datastructure-and-algorithm

一：哈密尔顿回路和哈密尔顿路径

1859 年，爱尔兰数学家哈密尔顿（Hamilton）提出了一个“周游世界”的游戏：

在一个正十二面体的二十个顶点上，标注了伦敦，巴黎，莫斯科等世界著名大城市，正十二面体的棱表示连接着这些城市的路线。要求游戏参与者从某个城市出发，把所有的城市都走过一次，且仅走过一次，然后回到出发点。这就是著名的哈密尔顿回路问题。

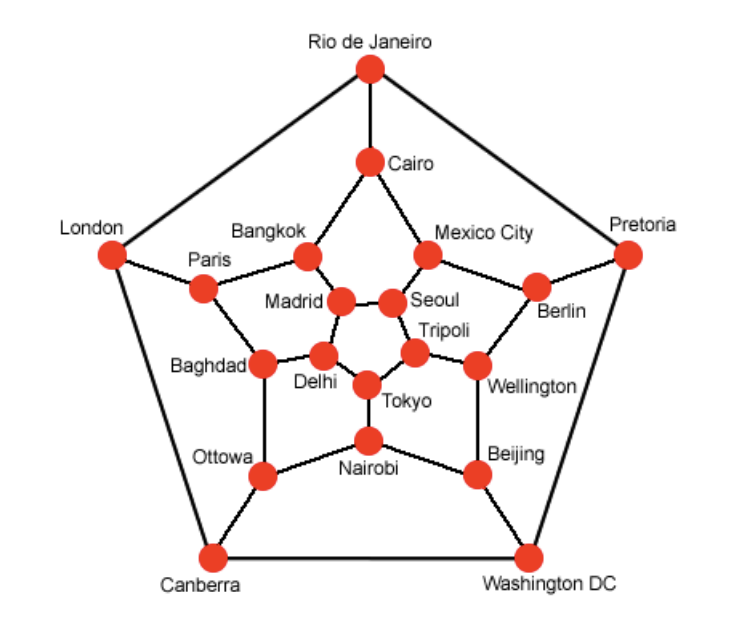
image.png
简而言之，哈密尔顿回路是指，从图中的一个顶点出发，沿着边行走，经过每个顶点恰好一次，之后再回到出发点。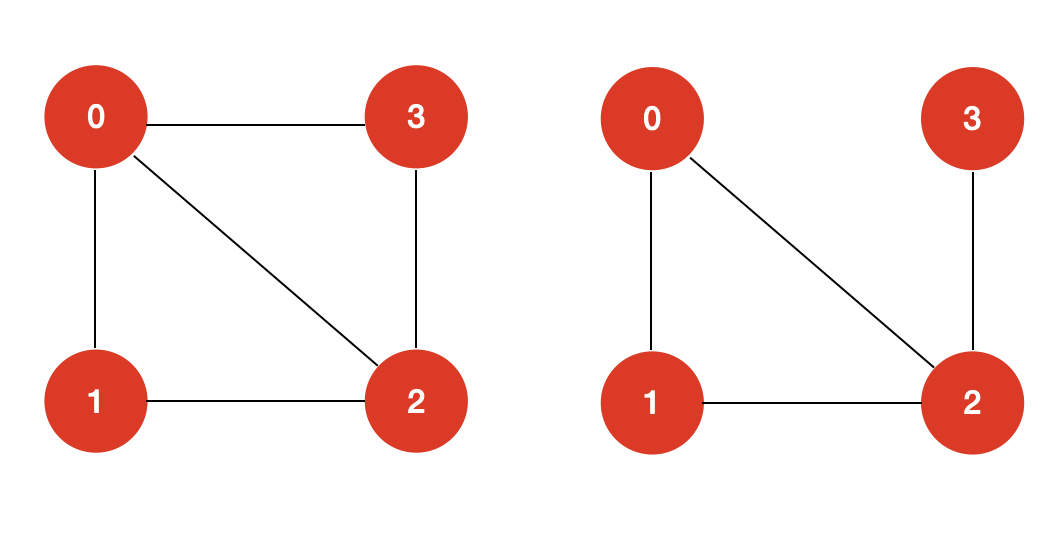
image.png
对于上面给出的示例图中，左图就存在哈密尔顿回路，而右图不存在哈密尔顿回路。

不过，右图是存在哈密尔顿路径的，哈密尔顿路径和哈密尔顿回路的定义只有一点不同，不同点在于哈密尔顿回路要求从起始点出发，遍历每个顶点且每个顶点仅遍历一次，并能回到起始点（回路）；哈密尔顿路径则是要求从起始点出发，遍历图的每个顶点且每个顶点仅遍历一次，不需要能回到起始点，也就是说，起始点和终止点不要求有一条边。

对于右边这个图来说，0->1->2->3 和 3->2->1->0 都是可行的哈密尔顿路径，但是，由于顶点 0 和顶点 3 之间没有边，所以不构成哈密尔顿回路。

二：求解哈密尔顿回路

代码链接🔗：1
代码链接🔗：2
代码链接🔗：3

如何求解哈密尔顿回路？

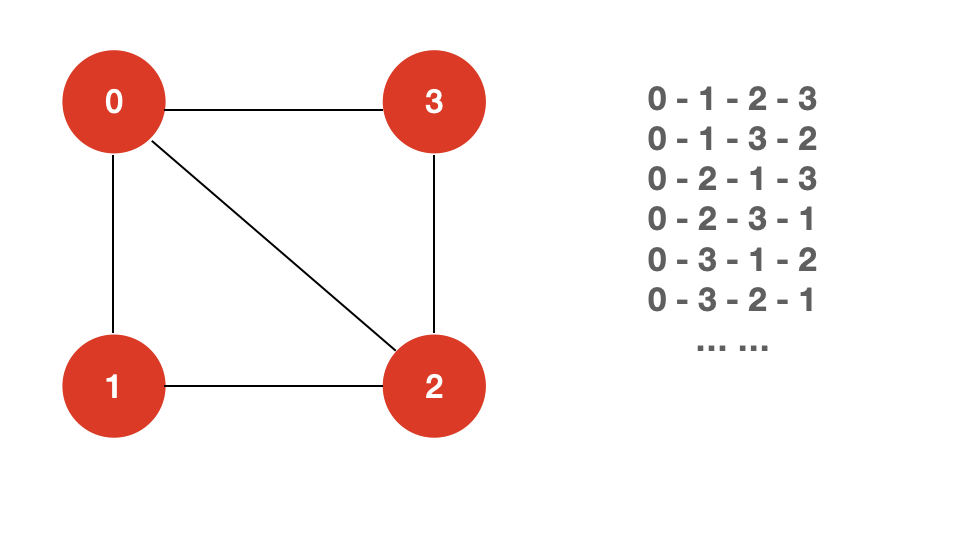
image.png
我们能想到最简单的方法就是暴力求解。类似于求解全排列问题，我们遍历图的每一个顶点 v，然后从 v 开始出发，看是否能够找到一条哈密尔顿回路。

我们知道，全排列问题的时间复杂度为 O(n!)。O(n!) 并不是一个多项式级别的复杂度。像 O(1)，O(nlogn)，O(n2) 这种级别的复杂度都是多项式级的复杂度，而像 O(an)，O(n!) 这样的复杂度是非多项式级的，其复杂度之高，往往在数据量极大的情况下，计算机是不能承受的。

像哈密尔顿回路问题，目前除了暴力求解这种方法之外，我们还没有找到一种多项式级别的算法来求解这道问题，通常像这种问题被称为 NP（Non-deterministic Polynomial） 难的问题。

求解哈密尔顿回路的算法采用回溯的思想来简化暴力破解，过程模拟在 PPT 中：

hamiltonLoop.key

代码如下：

  1. package com.github.datastructureandalgorithm.graph.chapter9;
  3. import java.util.ArrayList;
  4. import java.util.Collections;
  5. import java.util.List;
  7. public class HamiltonLoop {
  9.     private Graph G;
  10.     private boolean[] visited;
  11.     private int[] pre;
  12.     private int end; // end 表示 哈密尔顿回路是从 0 开始遍历到 end，end 是哈密尔顿回路的最后一个顶点
  14.     public HamiltonLoop(Graph G) {
  15.         this.G = G;
  16.         visited = new boolean[G.V()];
  17.         pre = new int[G.V()];
  18.         end = -1;
  19.         dfs(0, 0);
  20.     }
  22.     /**
  23.      * 对图进行深度优先遍历
  24.      *
  25.      * @param v
  26.      */
  27.     private boolean dfs(int v, int parent) {
  28.         visited[v] = true;
  29.         pre[v] = parent;
  31.         for (int w : G.adj(v)) {
  32.             if (!visited[w]) {
  33.                 if (dfs(w, v)) return true;
  34.             } else if (w == 0 && allVisited()) {
  35.                 end = v;
  36.                 return true;
  37.             }
  38.         }
  39.         visited[v] = false;
  40.         return false;
  41.     }
  43.     private boolean allVisited() {
  44.         for (boolean b : visited)
  45.             if (!b) return false;
  47.         return true;
  48.     }
  50.     /**
  51.      * 获取哈密尔顿回路
  52.      *
  53.      * @return
  54.      */
  55.     public List<Integer> result() {
  56.         List<Integer> res = new ArrayList<>();
  57.         if (end == -1) return res;
  58.         int cur = end;
  59.         while (cur != 0) {
  60.             res.add(cur);
  61.             cur = pre[cur];
  62.         }
  63.         res.add(0);
  64.         Collections.reverse(res);
  65.         return res;
  66.     }
  67. }

上面的代码中，我们的 allVisited 方法需要遍历一次 visited 数组。我们可以对我们的代码进行改进，设置一个变量 left，表示还有多少个顶点没有遍历到，每次的 dfs 过程中，都维护这个变量，直到 left == 0 时，说明所有的顶点都被遍历过了，改进的代码如下：

  1. package com.github.datastructureandalgorithm.graph.chapter9;
  3. import java.util.ArrayList;
  4. import java.util.Collections;
  5. import java.util.List;
  7. public class HamiltonLoop2 {
  8.     private Graph G;
  9.     private boolean[] visited;
  10.     private int[] pre;
  11.     private int end;
  12.     private int left;
  14.     public HamiltonLoop2(Graph G) {
  15.         this.G = G;
  16.         visited = new boolean[G.V()];
  17.         pre = new int[G.V()];
  18.         end = -1;
  19.         left = G.V();
  20.         dfs(0, 0);
  21.     }
  23.     /**
  24.      * 对图进行深度优先遍历
  25.      *
  26.      * @param v
  27.      * @param parent
  28.      * @return
  29.      */
  30.     private boolean dfs(int v, int parent) {
  31.         visited[v] = true;
  32.         pre[v] = parent;
  33.         left--;
  35.         for (int w : G.adj(v)) {
  36.             if (!visited[w]) {
  37.                 if (dfs(w, v)) return true;
  38.             } else if (w == 0 && left == 0) {
  39.                 end = v;
  40.                 return true;
  41.             }
  42.         }
  43.         visited[v] = false;
  44.         left++;
  45.         return false;
  46.     }
  48.     /**
  49.      * 获取哈密尔顿回路
  50.      *
  51.      * @return
  52.      */
  53.     public List<Integer> result() {
  54.         List<Integer> res = new ArrayList<>();
  55.         if (end == -1) return res;
  56.         int cur = end;
  57.         while (cur != 0) {
  58.             res.add(cur);
  59.             cur = pre[cur];
  60.         }
  61.         res.add(0);
  62.         Collections.reverse(res);
  63.         return res;
  64.     }
  65. }

三：求解哈密尔顿路径

代码连接🔗

求解哈密尔顿路径和求解哈密尔顿回路的算法整体框架是基本一致的。

对于求解哈密尔顿路径来说，起始点是谁很重要，同一个图，从有的起始点出发就存在哈密尔顿路径，从有的起始点出发就不存在哈密尔顿路径。所以，我们在算法设计中，构造函数需要用户显示地传入起始点。

我们的哈密尔顿路径求解的算法类 HamiltonPath 的构造函数是这样的：

  1. public HamiltonPath(Graph G,int s)

除了这一点外，求解哈密尔顿路径只需要保证，从起始点开始，所有的点被遍历过且仅被遍历一次，并不需要起始点和终止点之间有边。

所以，在 dfs 的逻辑中，我们只需要改变递归的终止条件即可：

  1. // 不需要保证终止点 v 和 起始点 s 存在一条边，即： G.hasEdge(v, s)
  2. if(left == 0 /*&& G.hasEdge(v, s)*/){
  3.     end = v;
  4.     return true;
  5. }

代码如下：

  1. package com.github.datastructureandalgorithm.graph.chapter9;
  3. import java.util.ArrayList;
  4. import java.util.Collections;
  5. import java.util.List;
  7. public class HamiltonPath {
  8.     private Graph G;
  9.     private int s;
  10.     private boolean[] visited;
  11.     private int[] pre;
  12.     private int end;
  13.     private int left;
  15.     public HamiltonPath(Graph G, int s) {
  16.         this.G = G;
  17.         this.s = s;
  18.         visited = new boolean[G.V()];
  19.         pre = new int[G.V()];
  20.         end = -1;
  21.         this.left = G.V();
  23.         dfs(s, s);
  24.     }
  26.     private boolean dfs(int v, int parent) {
  27.         visited[v] = true;
  28.         pre[v] = parent;
  29.         left--;
  31.         if (left == 0) {
  32.             end = v;
  33.             return true;
  34.         }
  36.         for (int w : G.adj(v)) {
  37.             if (!visited[w]) {
  38.                 if (dfs(w, v)) return true;
  39.             }
  40.         }
  42.         visited[v] = false;
  43.         left++;
  44.         return false;
  45.     }
  47.     /**
  48.      * 返回哈密尔顿路径
  49.      *
  50.      * @return
  51.      */
  52.     public List<Integer> result() {
  53.         List<Integer> res = new ArrayList<>();
  54.         if (end == -1) return res;
  56.         int cur = end;
  57.         while (cur != s) {
  58.             res.add(cur);
  59.             cur = pre[cur];
  60.         }
  61.         res.add(s);
  62.         Collections.reverse(res);
  63.         return res;
  64.     }
  65. }

四：LeetCode 上的哈密尔顿问题：不同路径III

980. 不同路径 III

代码链接🔗

本题是一道经典的求解哈密尔顿路径问题，使用经典的回溯法即可解决，就不再赘述了，详情请见代码：

  1. class Solution {
  2.     private int[][] grid;
  3.     private int r, c;
  4.     private boolean[][] visited;
  5.     private int left;
  6.     private int start;
  7.     private int end;
  8.     private int[][] dirs = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
  10.     public int uniquePathsIII(int[][] grid) {
  11.         this.grid = grid;
  12.         this.r = grid.length;
  13.         this.c = grid[0].length;
  14.         this.visited = new boolean[r][c];
  15.         this.left = r * c;
  17.         for (int i = 0; i < r; i++)
  18.             for (int j = 0; j < c; j++)
  19.                 if (grid[i][j] == 1) {
  20.                     start = i * c + j;
  21.                     grid[i][j] = 0;
  22.                 } else if (grid[i][j] == 2) {
  23.                     end = i * c + j;
  24.                     grid[i][j] = 0;
  25.                 } else if (grid[i][j] == -1) {
  26.                     left--;
  27.                 }
  29.         return dfs(start);
  30.     }
  32.     int dfs(int s) {
  33.         int x = s / c;
  34.         int y = s % c;
  36.         visited[x][y] = true;
  37.         left--;
  39.         if (s == end && left == 0) {
  40.             // 回溯
  41.             visited[x][y] = false;
  42.             left++;
  43.             return 1;
  44.         }
  46.         int res = 0;
  47.         for (int d = 0; d < 4; d++) {
  48.             int nextX = x + dirs[d][0];
  49.             int nextY = y + dirs[d][1];
  51.             if (isValid(nextX, nextY) && !visited[nextX][nextY] && grid[nextX][nextY] != -1) {
  52.                 int next = nextX * c + nextY;
  53.                 res += dfs(next);
  54.             }
  55.         }
  57.         // 回溯
  58.         visited[x][y] = false;
  59.         left++;
  61.         return res;
  62.     }
  64.     private boolean isValid(int x, int y) {
  65.         return x >= 0 && x < r && y >= 0 && y < c;
  66.     }
  67. }

五：状态压缩

哈密尔顿回路状态压缩代码链接🔗
哈密尔顿路径状态压缩代码链接🔗

在我们的代码中，一直都使用布尔型的 visited 数组来记录图中的每一个顶点是否有被遍历过。在算法面试中，对于像哈密尔顿回路/路径这样的 NP 难问题，通常都会有输入限制，一般情况下，求解问题中给定的图不会超过 30 个顶点。

我们可以使用状态压缩的思想，将 visited 数组简化成一个数字。我们知道一个 int 型的数字有 32 位，每一位不是 1 就是 0，这正好对应了布尔型的 true 和 false。

来看一下我们的代码：
image.png
我们的 dfs 中，涉及到 visited 数组的操作共有三处，这三处对布尔型数组的赋值操作可以转换为位运算的操作：

  • 如果第 i 位为 0，设为 1；

    1. visited + (1 << i);

  • 看其第 i 位是否为 1；

    1. visited & (1 << i) == 0 ?

  • 如果第 i 位为 1，设为 0；

    1. visited - (1 << i) == 0;

    具体改动代码请参考链接。

六：记忆化搜索

我们来看一下，我们当前的算法类有什么问题：

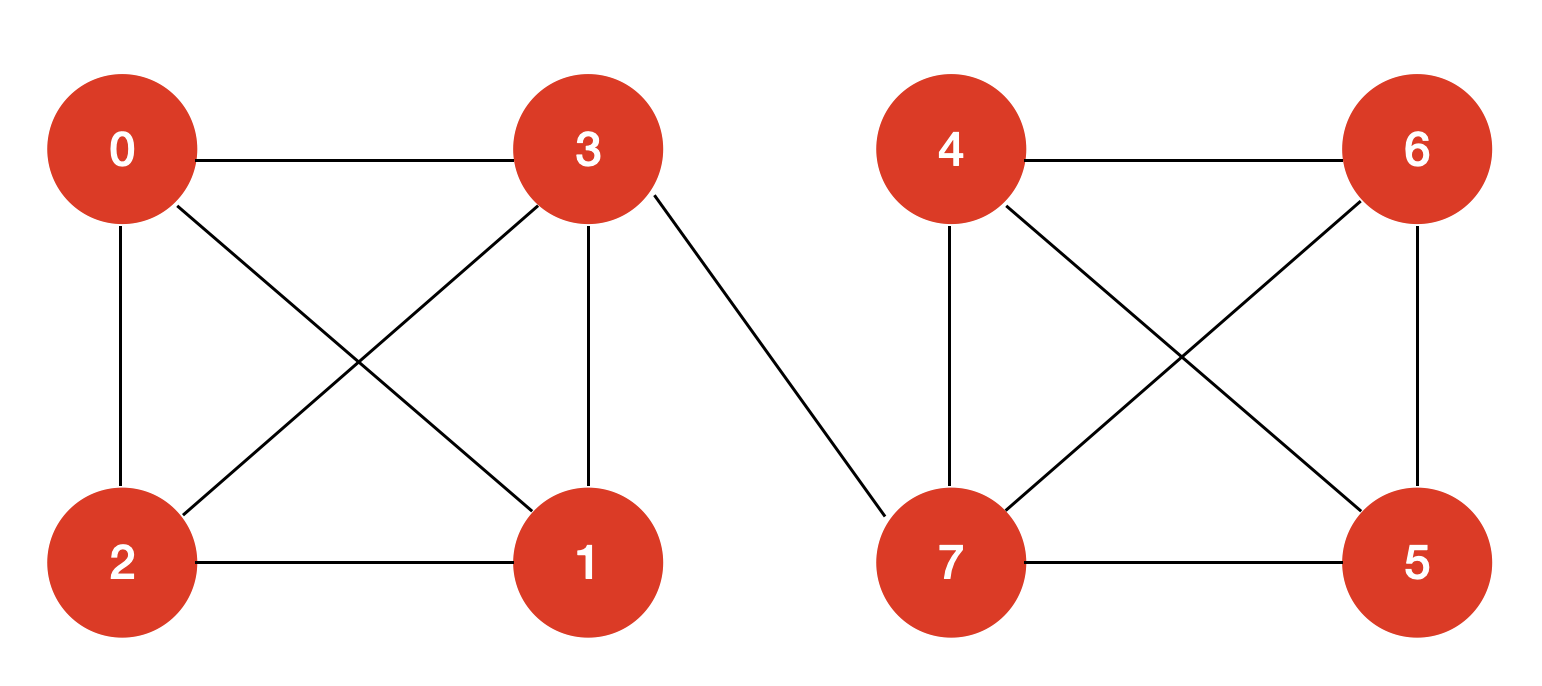
image.png
对于上面这个图来说，因为顶点 3 和顶点 4 之间只有一条边，所以肯定是不会构成一条哈密尔顿回路的。

但是我们的回溯算法在遍历顶点时，不会提前返回结果，譬如：

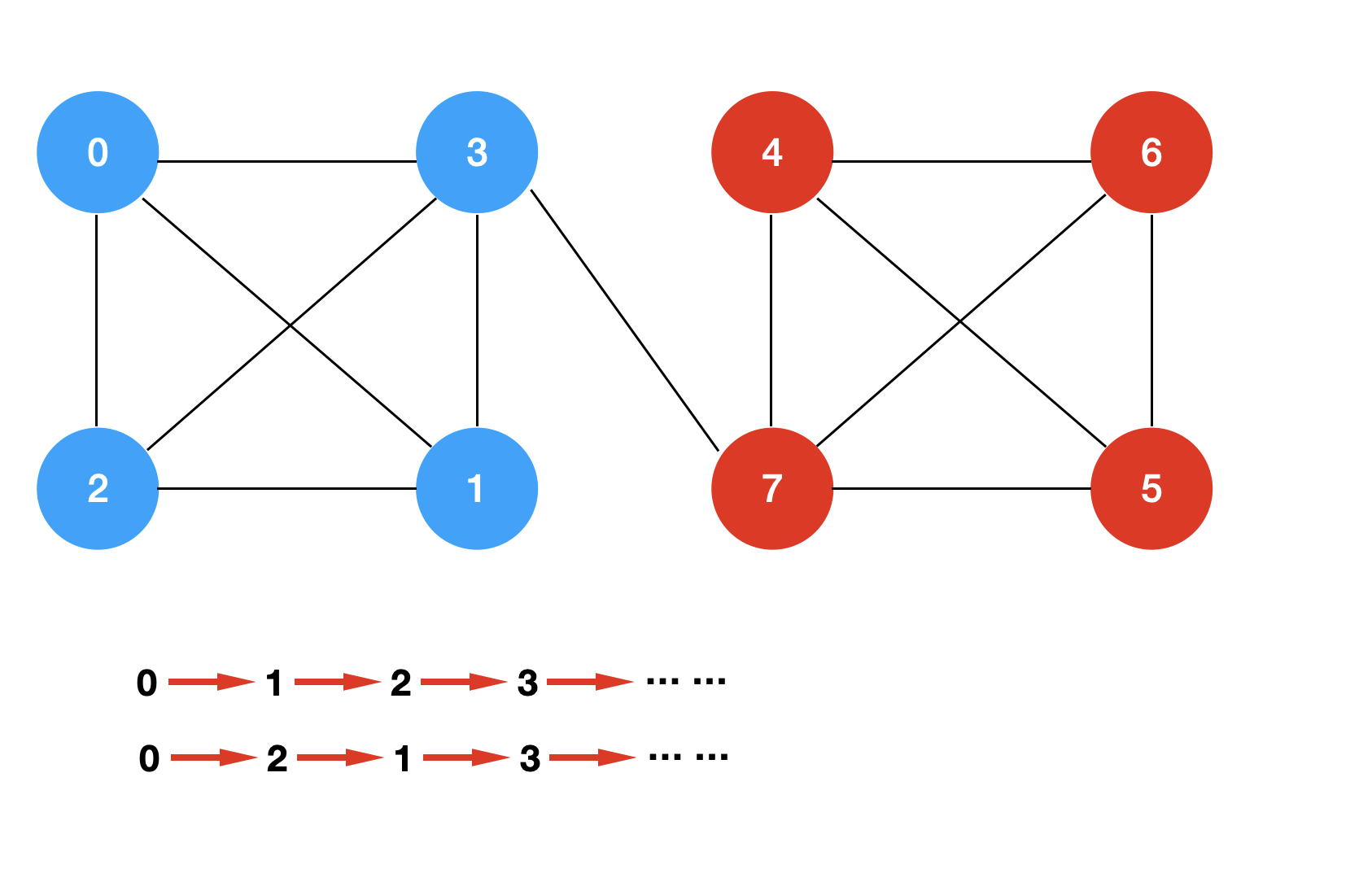
image.png
依次遍历 0 -> 1 -> 2 -> 3 … 这些顶点，图中，0，1，2，3 这些顶点都已经被访问过，所以我对这些顶点标记为蓝色；我们发现找不到一条哈密尔顿回路。

而下一次的遍历，则会依次遍历 0 -> 2 -> 1 -> 3 这些顶点，我们遍历左侧的图的最后一个顶点仍然为 3，且左侧的四个顶点都已经被遍历过。这个时候我们知道，其实可以提前返回结果，但是我们的算法类不具有这个功能。

要想实现提前返回这个功能，就需要在我们设计的算法类中加入记忆化搜索。

实现记忆化搜索非常简单，在我们设计算法类中，再开辟一个数组memory[1 << G.V()][G.V()] 对应着 dfs 的方法签名中的 dfs(visited,v)。我们开辟的 memory 将会记录 visited 和 v 这个组合有没有计算过，像上面给定的示例，两次遍历中，左侧的四个顶点都已经被访问过了，且最后遍历都落到了 3 这个顶点，我们在第一次遍历时，就可以记录这个状态，等到第二次遍历时，发现这个状态已经出现过，就可以避免重复遍历。

添加了记忆化搜索的时间复杂度和回溯法的时间复杂度不同，记忆化搜索的时间复杂度为：8、哈密尔顿问题和状态压缩 - 图7相比于回溯法的 8、哈密尔顿问题和状态压缩 - 图8 来讲实际上各有利弊，因为我们的回溯法中也有剪枝的过程。但是，整体上来讲，随着 n 的不断增大，8、哈密尔顿问题和状态压缩 - 图9 的复杂度是要高于 8、哈密尔顿问题和状态压缩 - 图10 的。

现在，我们针对于 LeetCode 980. 不同路径 III 这个问题，来添加上记忆化搜索，看一下执行的效率如何。

  1. import java.util.Arrays;
  3. /**
  4.  * LeetCode 980.不同路径 III：https://leetcode-cn.com/problems/unique-paths-iii/
  5.  * <p>
  6.  * 添加了对 visited 状态压缩的优化
  7.  * 添加了记忆化搜索
  8.  */
  9. public class Solution2 {
  10.     private int[][] grid;
  11.     private int r, c;
  12.     private int left;
  13.     private int start;
  14.     private int end;
  15.     private int[][] dirs = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
  16.     private int[][] memory;
  18.     public int uniquePathsIII(int[][] grid) {
  19.         this.grid = grid;
  20.         this.r = grid.length;
  21.         this.c = grid[0].length;
  22.         this.left = r * c;
  23.         int visited = 0;
  25.         this.memory = new int[1 << r * c][r * c];
  27.         for (int i = 0; i < memory.length; i++)
  28.             Arrays.fill(memory[i], -1);
  30.         for (int i = 0; i < r; i++)
  31.             for (int j = 0; j < c; j++)
  32.                 if (grid[i][j] == 1) {
  33.                     start = i * c + j;
  34.                     grid[i][j] = 0;
  35.                 } else if (grid[i][j] == 2) {
  36.                     end = i * c + j;
  37.                     grid[i][j] = 0;
  38.                 } else if (grid[i][j] == -1) {
  39.                     left--;
  40.                 }
  42.         return dfs(visited, start);
  43.     }
  45.     int dfs(int visited, int s) {
  46.         // 说明该状态已经被记录过
  47.         if (memory[visited][s] != -1)
  48.             return memory[visited][s];
  50.         visited += (1 << s);
  51.         left--;
  53.         if (s == end && left == 0) {
  54.             // 回溯
  55.             visited -= (1 << s);
  56.             left++;
  57.             memory[visited][s] = 1;
  58.             return 1;
  59.         }
  61.         int res = 0;
  62.         int x = s / c;
  63.         int y = s % c;
  64.         for (int d = 0; d < 4; d++) {
  65.             int nextX = x + dirs[d][0];
  66.             int nextY = y + dirs[d][1];
  67.             int next = nextX * c + nextY;
  68.             if (isValid(nextX, nextY) && (visited & (1 << next)) == 0 && grid[nextX][nextY] != -1) {
  69.                 res += dfs(visited, next);
  70.             }
  71.         }
  73.         // 回溯
  74.         visited -= (1 << s);
  75.         left++;
  76.         memory[visited][s] = res;
  77.         return res;
  78.     }
  80.     private boolean isValid(int x, int y) {
  81.         return x >= 0 && x < r && y >= 0 && y < c;
  82.     }
  83. }

在我的电脑上，使用回溯算法的执行效率为：

image.png
添加了记忆化搜索之后，算法的执行效率为：
image.png

对于 LeetCode 上这道问题，添加了记忆化搜索之后，我们提交的代码执行时间实际上是更慢了，原因就在于，我们开辟 memory 数组的时间上。虽然我们的算法解决了重复遍历的情况，但是对于没有那么多重复的情况下，我们的记忆化搜索也不一定有回溯更快，这一点望大家可以了解。