【数据结构与算法基础】代码仓库：https://github.com/jinrunheng/datastructure-and-algorithm

一：无向图的联通分量的个数

该图中具有两个联通分量：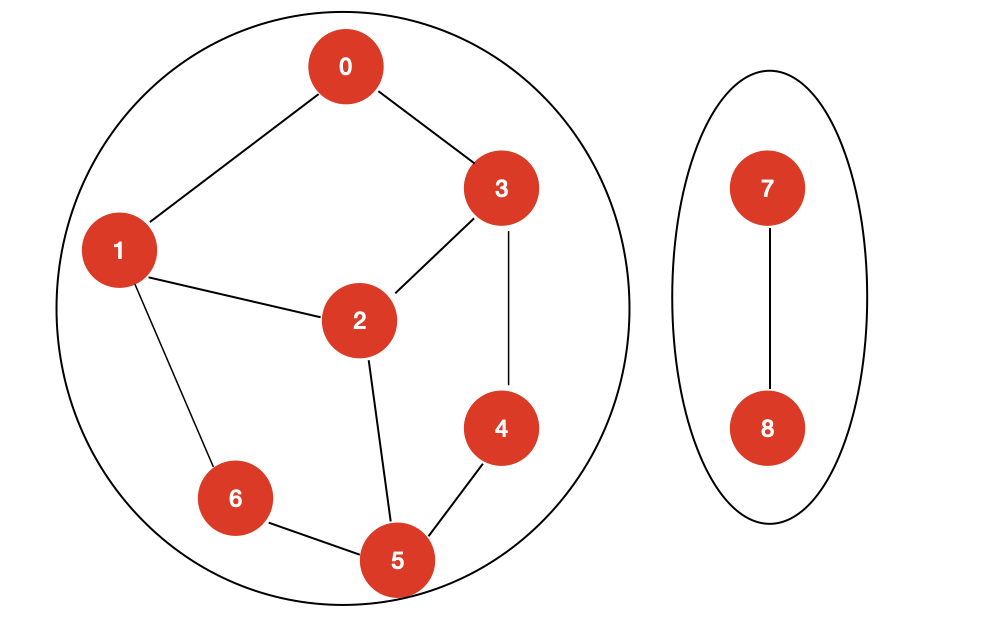
image.png
求解一个无向图的联通分量的个数实际上是非常简单的，伪代码如下：

  1. visited[0…V] = false;
  3. int ccCount = 0; // Connected Component Count
  5. for(int v = 0; v < V; v++) {
  6.     if(!visited[v]) {
  7.         dfs(v);
  8.         ccCount++;
  9.     }
  10. }
  12. dfs(int v) {
  13.     visited[v] = true;
  14.     for(int w : adj(v))
  15.         if(!visited[w])
  16.             dfs(w);
  17. }

二：求解联通分量

代码链接🔗

除了求解一个无向图中包含多少个联通分量，有的时候，我们还需要知道一个联通分量中包含哪些顶点。

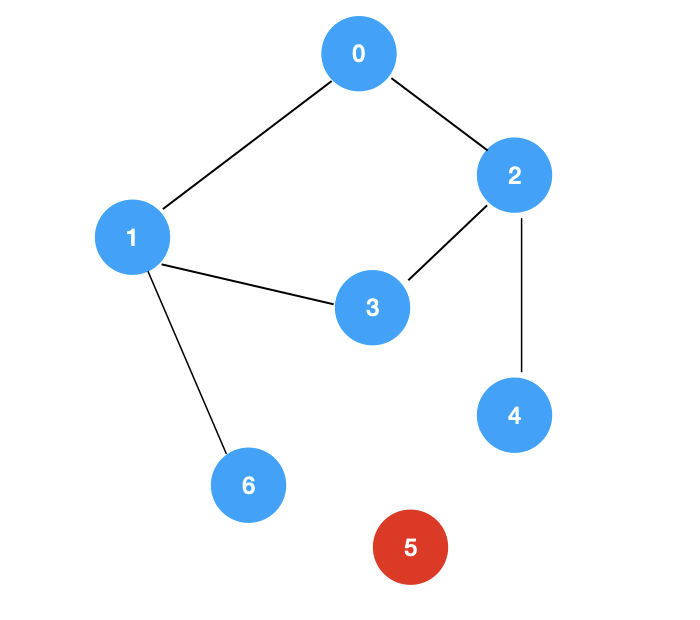
image.png
上面这个图中，有两个联通分量，其中顶点0,1,2,3,4,6 属于一个联通分量，顶点5 单独属于一个联通分量。

我们可以对代码进行改进，原本的 visited 数组存储是 boolean 值，表示这个顶点是否有被访问过；我们可以将这个数组改进为一个 int 型数组，如果该数组对应的数字为 -1，则代表该顶点没有被访问过；如果在遍历的时候，这些顶点同属于一个联通分量，我们就在数组中存储对应的 ccCount 信息。

改进的伪代码如下：

  1. visited[0…V] = -1;
  3. int ccCount = 0; // Connected Component Count
  5. for(int v = 0; v < V; v++) {
  6.     if(visited[v] == -1) {
  7.         dfs(v,ccCount);
  8.         ccCount++;
  9.     }
  10. }
  12. dfs(int v,int ccId) {
  13.     visited[v] = ccId;
  14.     for(int w : adj(v))
  15.         if(visited[w] == -1)
  16.             dfs(w,ccId);
  17. }

这样，我们就将同属于一个联通分量的顶点在 visited 数组中标记了相同的信息。对于示例给出的图，遍历该图后的visited 数组为：

  1. [0 0 0 0 0 1 0]

可以看到，顶点0,1,2,3,4,6 属于一个联通分量，在 visited 数组中被标记为 0，顶点5 单独属于一个联通分量，在 visited 数组中被标记为 1。

进而，我们就可以设计出更多的方法接口，譬如：判断两个顶点是否在一个联通分量中：

  1. public boolean isConnected(int v, int w) {
  2.     return visited[v] == visited[w];
  3. }

返回图的联通分量的顶点集合：

  1. public List<Integer>[] components() {
  2.     List<Integer>[] res = new ArrayList[ccCount];
  3.     for (int i = 0; i < ccCount; i++)
  4.         res[i] = new ArrayList<>();
  6.     for (int v = 0; v < G.V(); v++)
  7.         res[visited[v]].add(v);
  9.     return res;
  10. }

三：单源路径问题

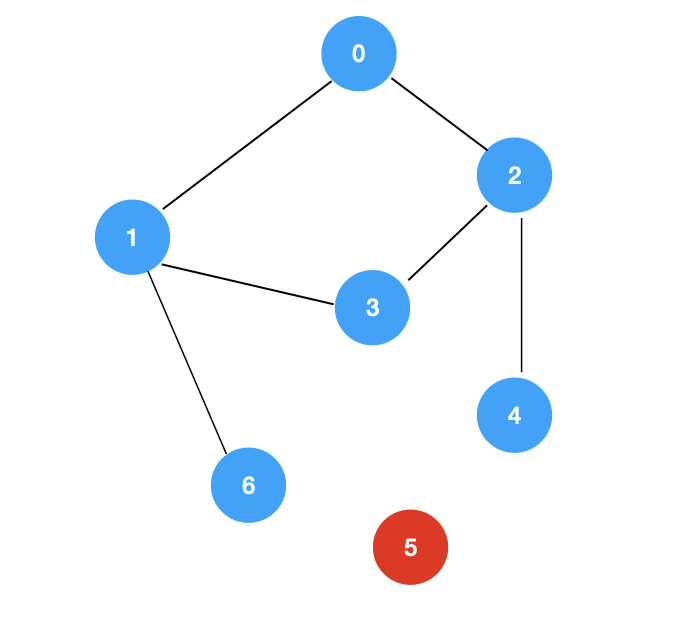
image.png
如果给定一个无向图，问图中的任意两点是否存在路径，那么这个问题实际上非常简单，我们只需要判断两个顶点是否在一个联通分量中即可。

如果要我们求出两个顶点之间任意一条路径是什么，这个问题该如何求解呢？

现在我们来回顾一下图的 dfs 遍历

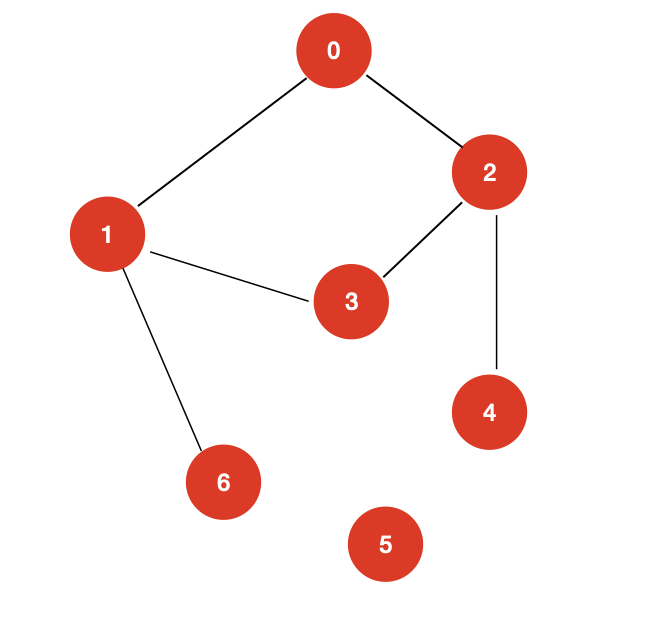
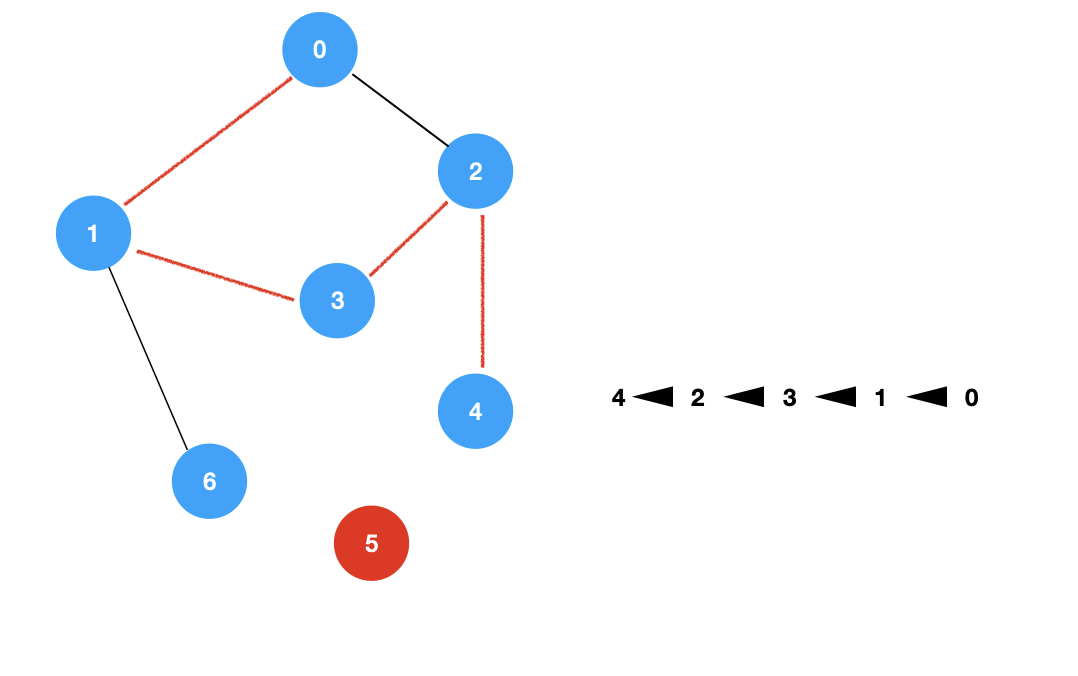
image.png
对于这个图，我们从 0 开始进行 dfs 遍历

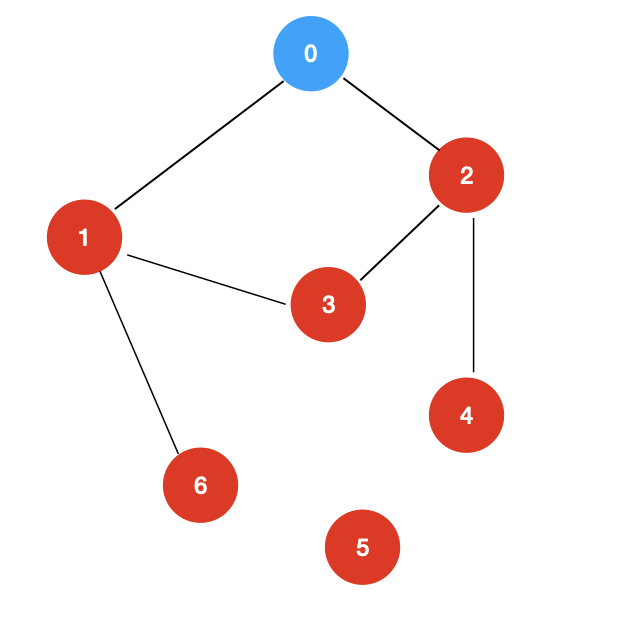
image.png
遍历到 1 这个顶点，我们可以记录一个信息 1 <- 0，表示 1 这个顶点是通过 0 这个顶点而来的。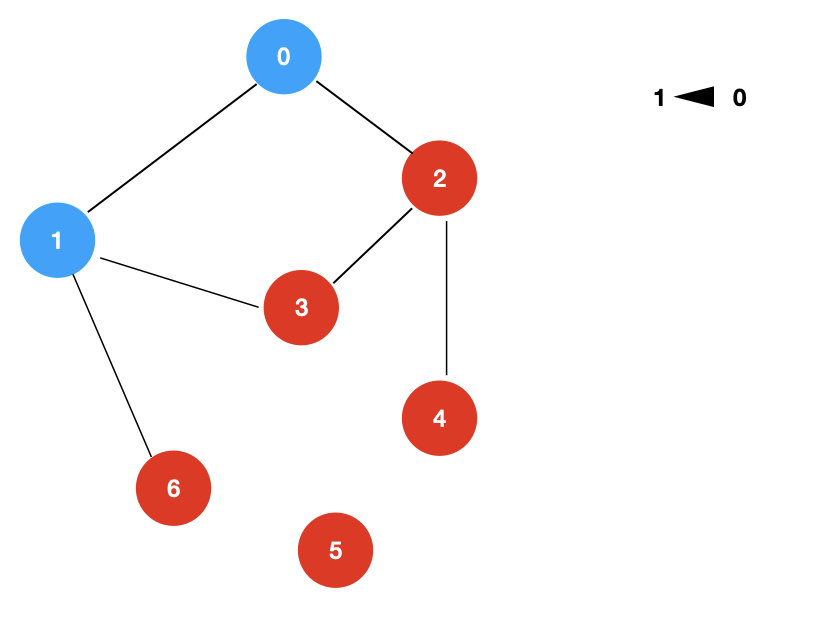
image.png
后续的整个过程记录后的结果如下：

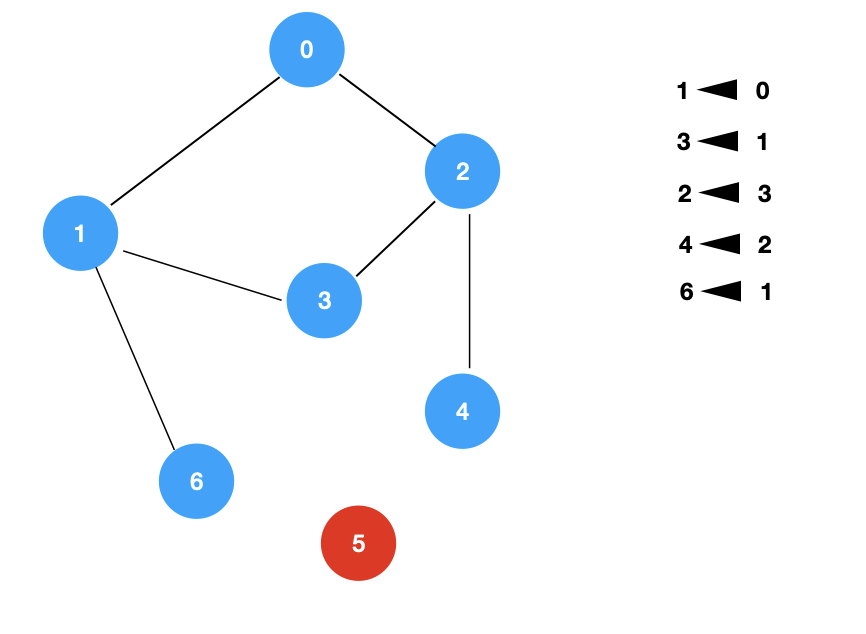
image.png
我们可以通过记录一个数组 pre，数组 pre 记录每一个顶点是通过哪一个顶点而获得的，源顶点记录的是自己，即 pre[0] = 0。

数组 pre 如下：

  1. [0 0 3 1 2 1]

如果想要获得从顶点 0 到 顶点 4 的一条路径，通过我们记录的数组 pre，就可以获得这条路径。

image.png

单源路径问题的编程实现

代码链接🔗

代码请点击链接进行查看，这里就不再赘述了。

四：所有点对路径问题

代码链接🔗

有了单源路径问题的铺垫，我们很自然地想到，是否可以求出图中任意两点的路径。

其实思路非常简单，我们只要对图中的每一个顶点都实现一遍单源路径问题就好了。代码非常简单，请点击链接进行查看，这里就不再赘述了。

五：路径问题的优化

代码链接🔗

我们来回顾一下，单源路径的代码逻辑：

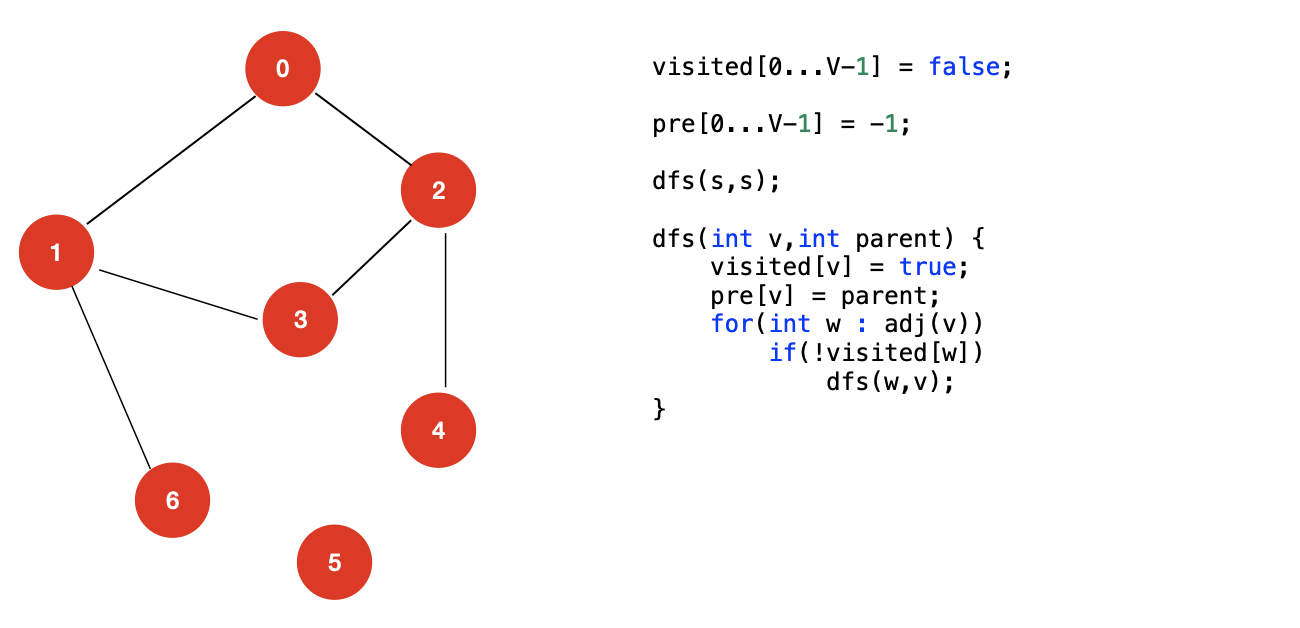
image.png
如果要求得顶点 0 和顶点 1 之间的路径，使用上面的逻辑，我们就会发现，整个 dfs 的过程实际上将顶点 0 和同一个联通分量的所有顶点都遍历了一次，但实际上，只需要求出顶点 0 和顶点 1 之间的路径就可以了。所以，我们可以优化我们的代码逻辑，让递归可以提前结束。

我们的代码逻辑上作出的改进如下：

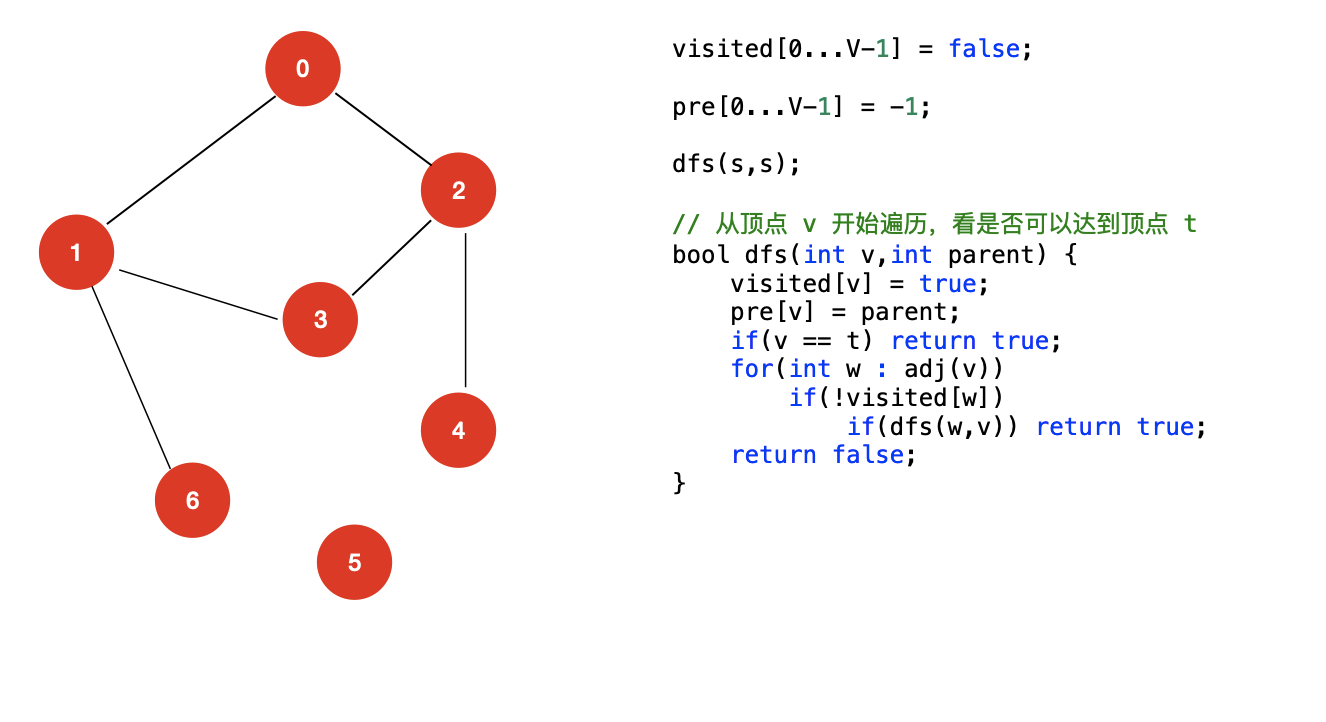
image.png
对于该算法，复杂度仍然为 O(V)，因为最差的情况下，我们还是需要遍历所有的顶点，但是整体上，因为我们控制递归可以提前返回，如果检测譬如：顶点 0 和顶点 1 之间的路径，我们仅仅需要遍历 0，1 这两个顶点，而不需要遍历所有的顶点，在性能还是有一定的提升。

六：无向图的环检测

代码链接🔗

检测无向图中的环

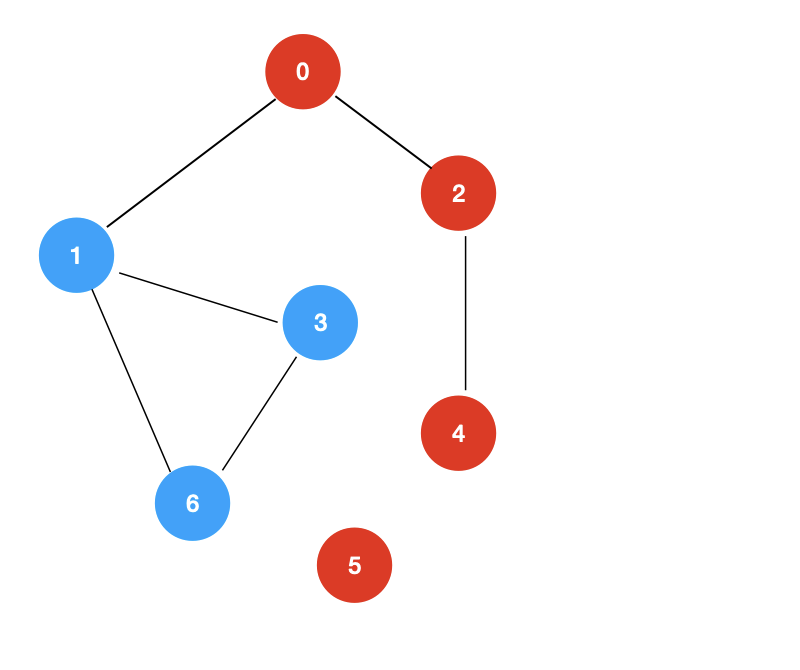
image.png
对于上面这个无向图，我们从顶点 0 开始出发，依次遍历到顶点 1，3，6，当遍历到顶点 6 时，我们又回到了顶点 1，此时，我们发现，顶点 1 是一个已经被访问过的节点，并且顶点 1 并不是当前的顶点 6 的上一个节点，这个时候，就说明我们找到了一个环。

通过上面分析，我们得到结论：找到一个已经被访问过的节点，并且这个节点不是当前节点的的上一个节点，这也就说明我们找到了一个环。

伪代码如下：

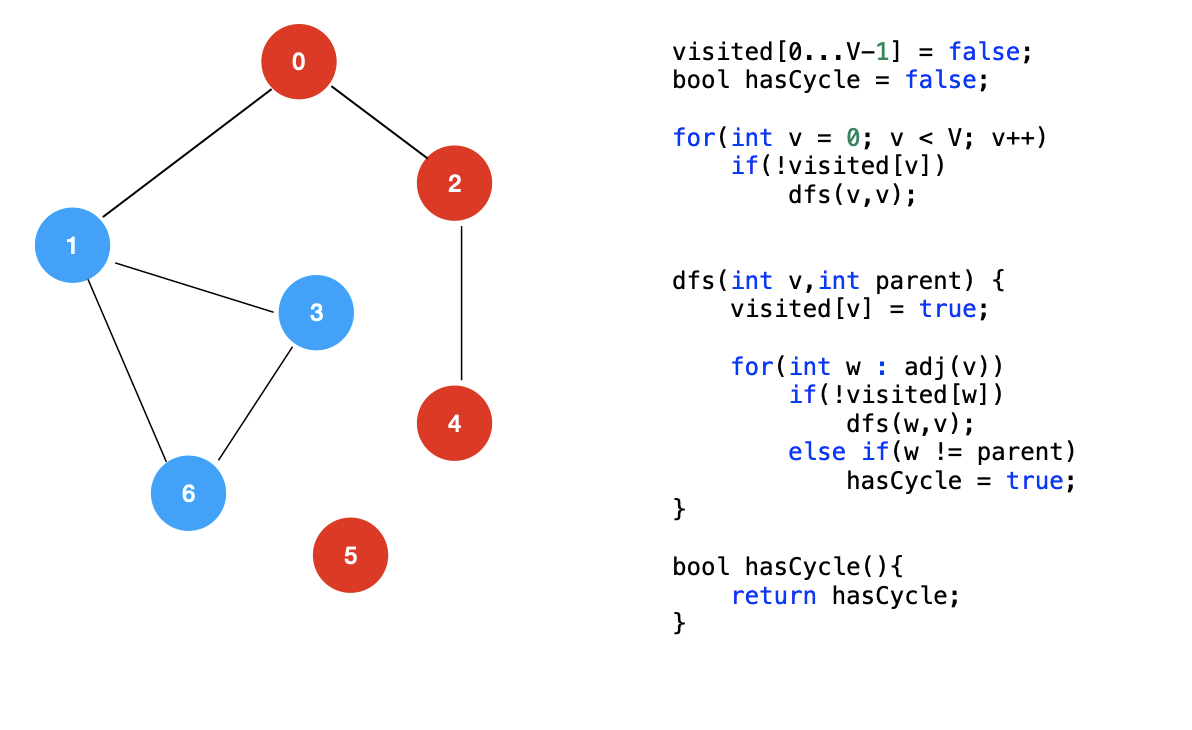
image.png

除了可以检测无向图中的环，我们还可以检测图是否是一棵树，当一个图只有一个联通分量，且图中无环时，这个图就是一棵树，代码链接如下：

代码链接🔗

七：二分图检测

代码链接🔗

什么是二分图？
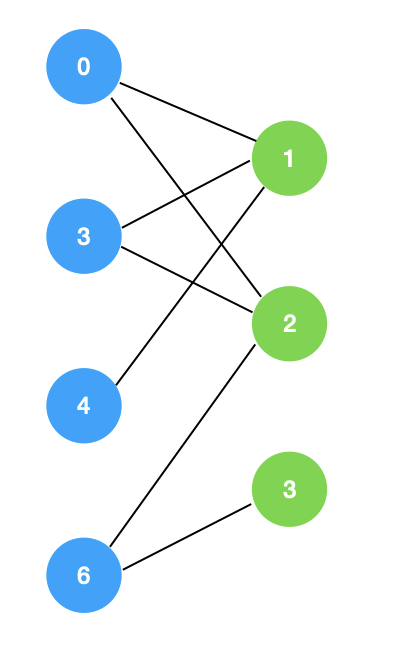
image.png
二分图又称作为二部图，是图论中的一种特殊模型，其具有以下的特性：

  • 顶点 V 可以分成不相交的两部分
  • 所有的边的两个端点隶属不同的部分

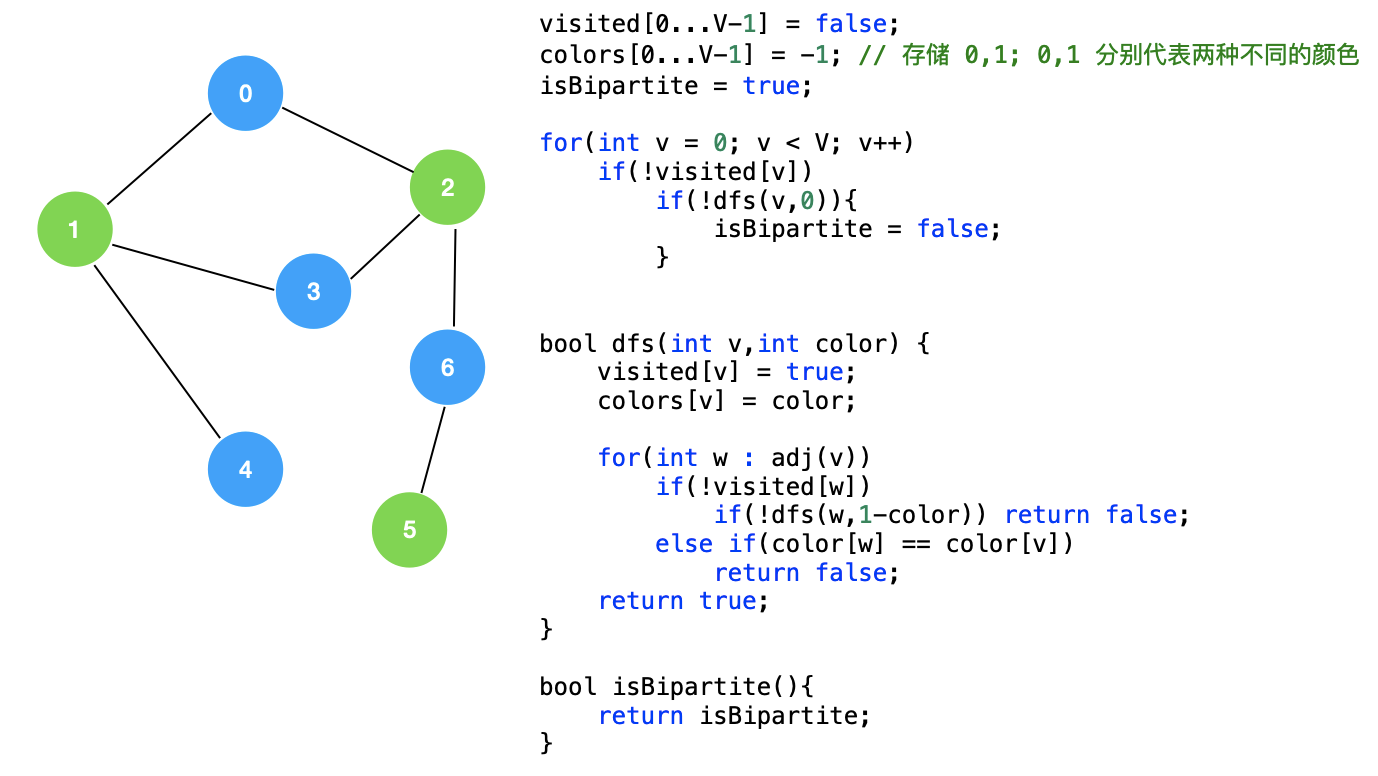
为了让上面的二分图明显被看出，我给出了上图这种蓝绿节点左右排步的样子，我们再来看一个图：

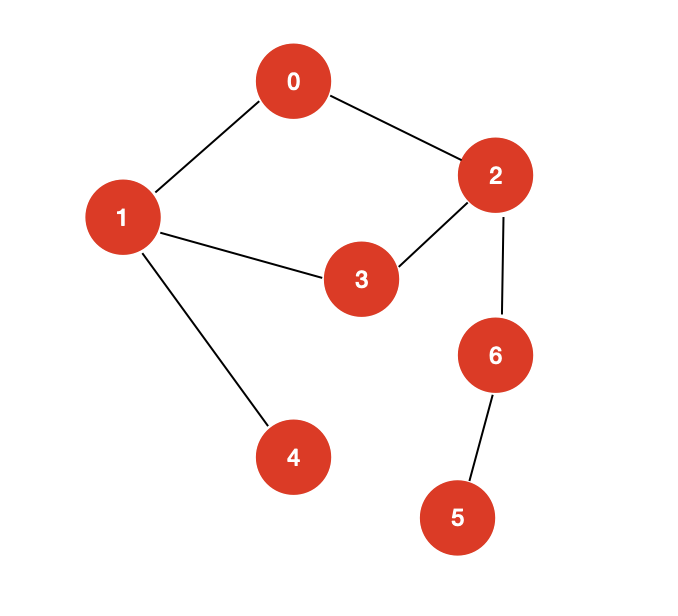
image.png
现在，让我们判断，上面的图是否是一个二分图？

这就是一个二分图检测问题，二分图的检测的核心就是在 dfs 遍历的过程中染色。我们再来回顾一下二分图的特性，其中有一条为 “所有的边的两个端点隶属不同的部分”，我们可以在 dfs 遍历的过程中，对顶点进行“染色”，如果染色后，满足二分图的特性，说明该图就是一个二分图。

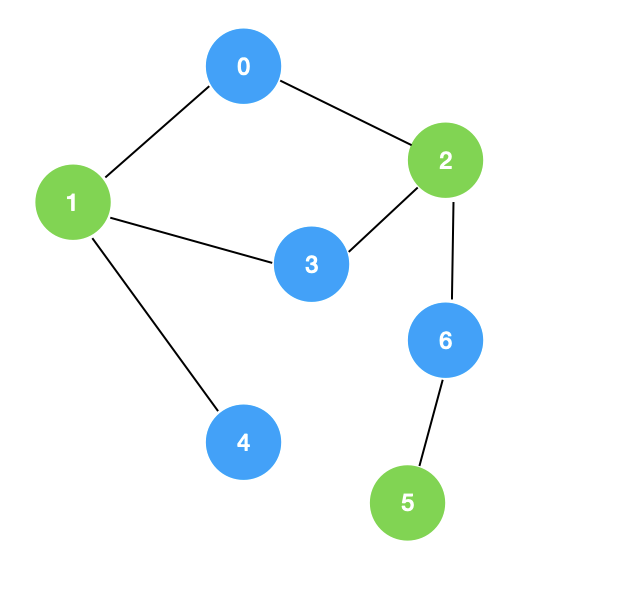
image.png

该算法思路其实非常的简单，伪代码如下：

image.png