4、图的广度优先遍历

【数据结构与算法基础】代码仓库：https://github.com/jinrunheng/datastructure-and-algorithm

一：从树的广度优先遍历到图的广度优先遍历

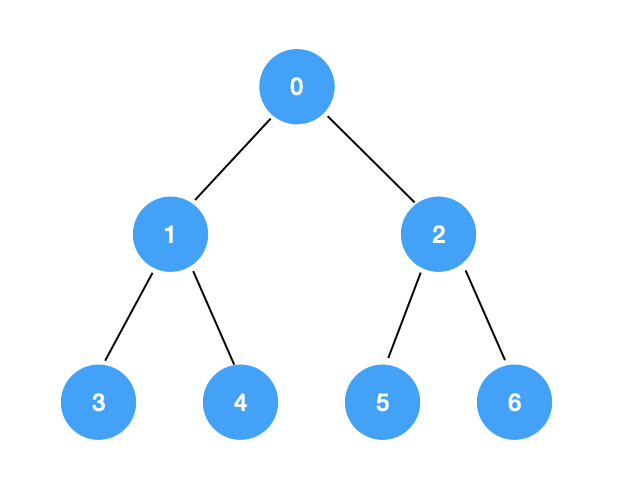
对于一棵树，广度优先遍历是使用一个队列来实现的，其伪代码如下：

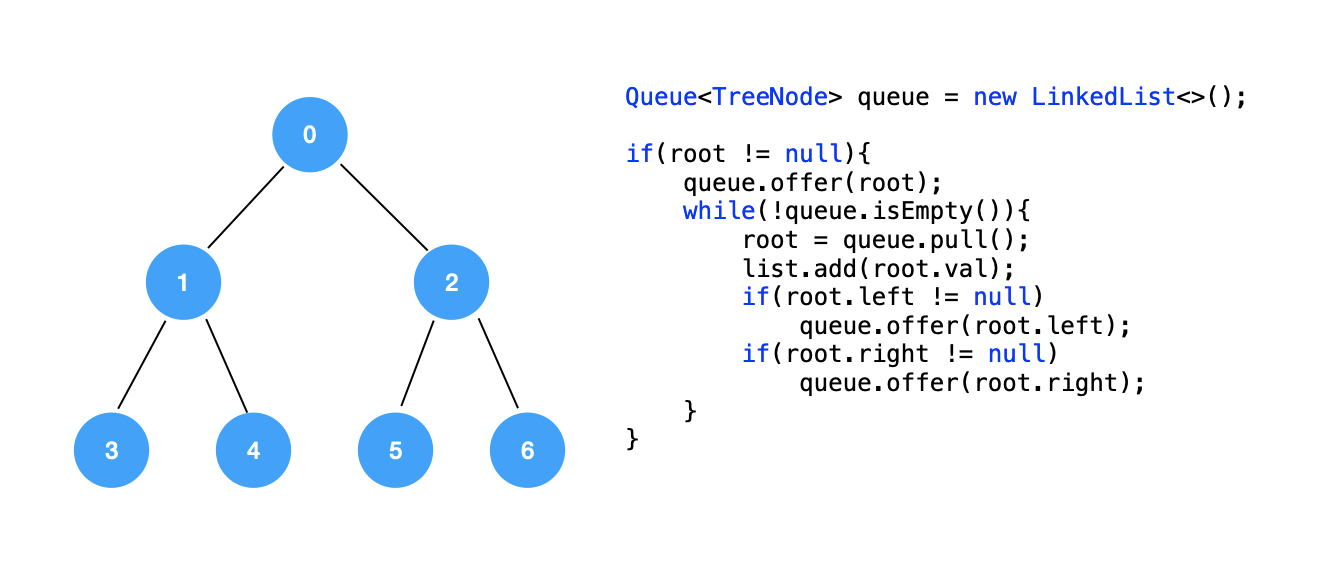
其实图的广度优先遍历和树的优先遍历的本质是一样的，只不过，和 DFS 一样，图的广度优先遍历也需要记录哪个节点被遍历过。

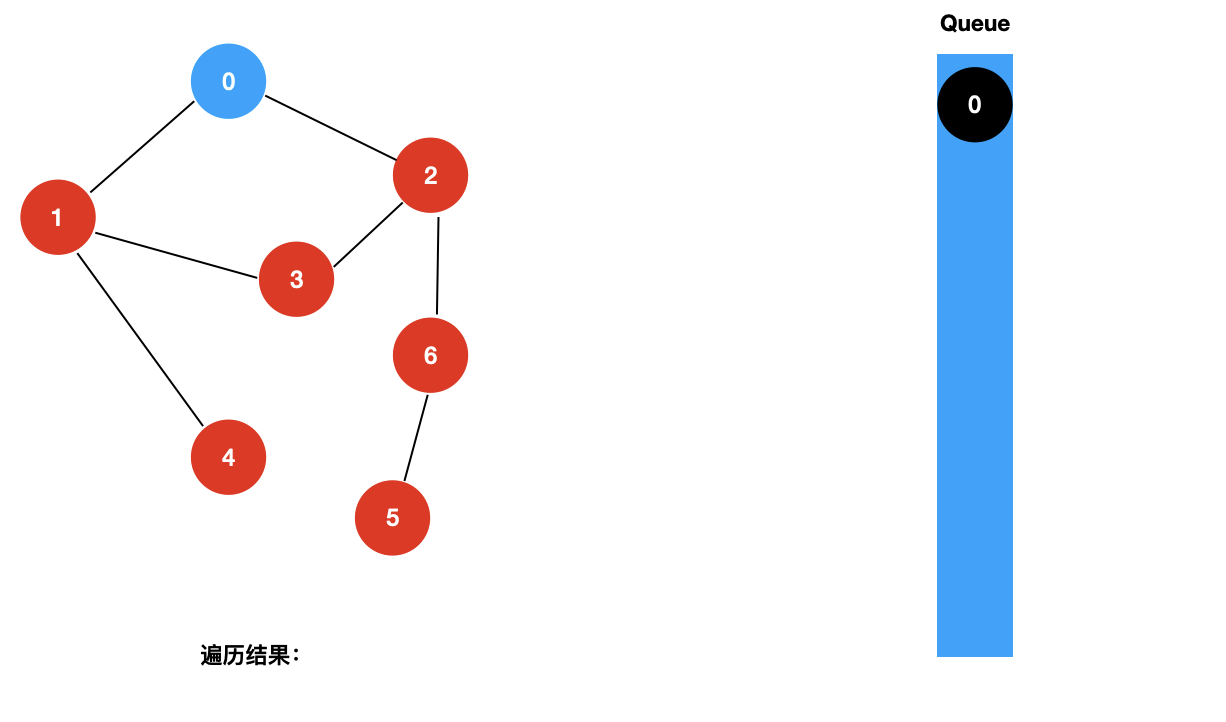
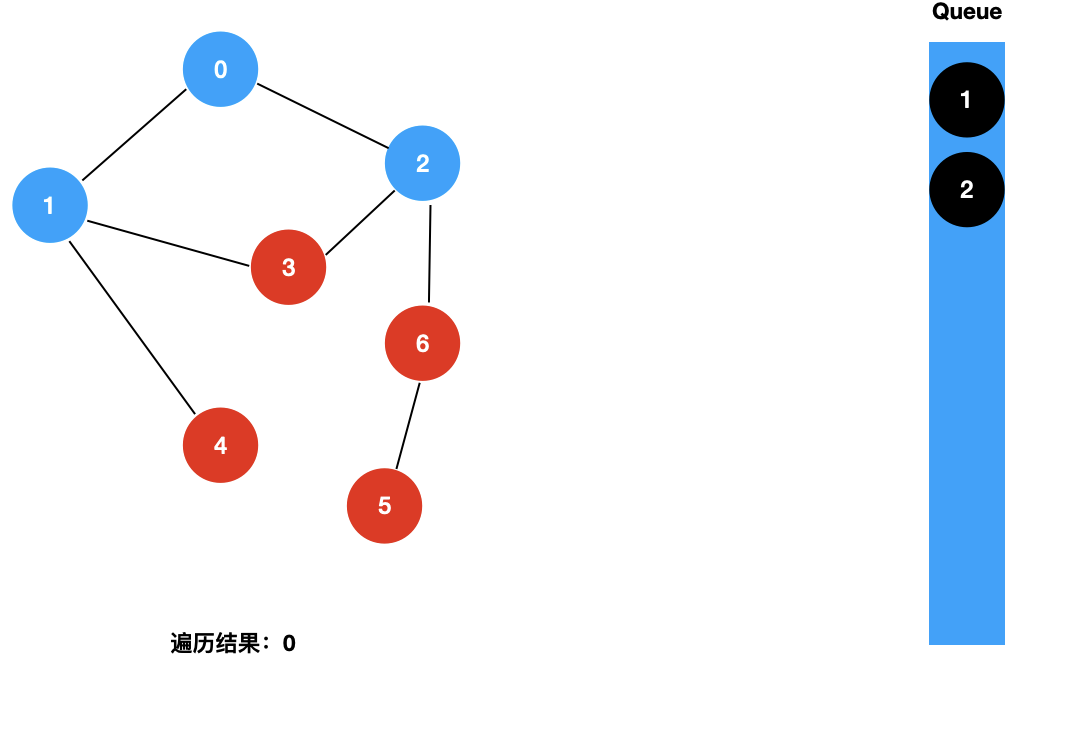
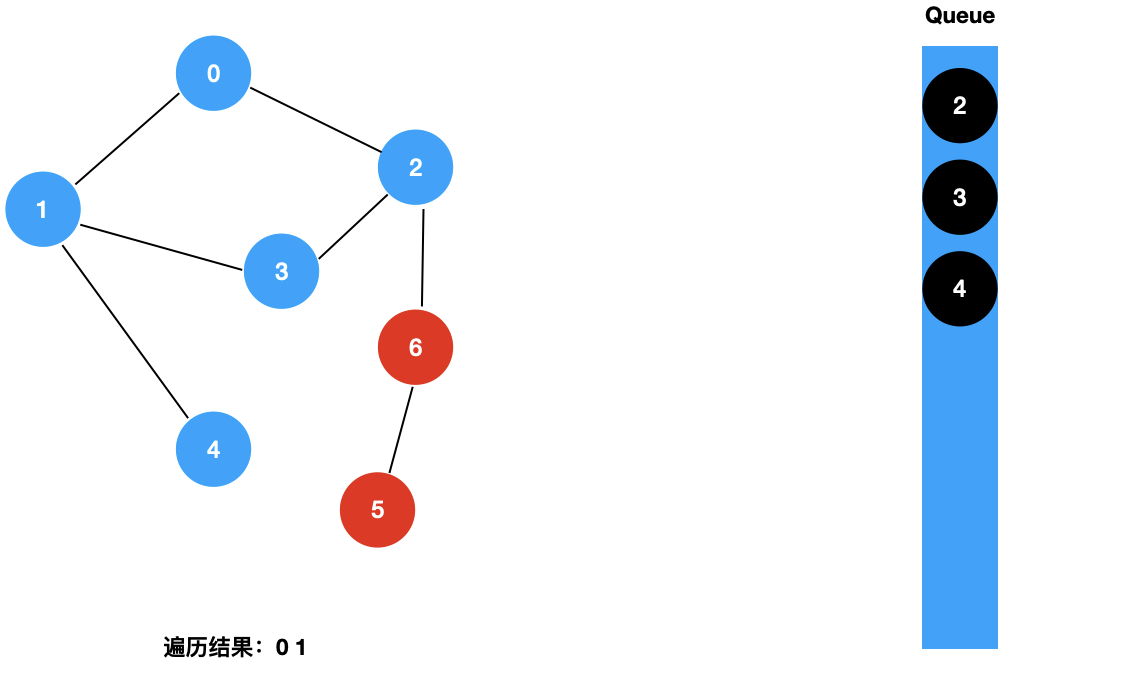
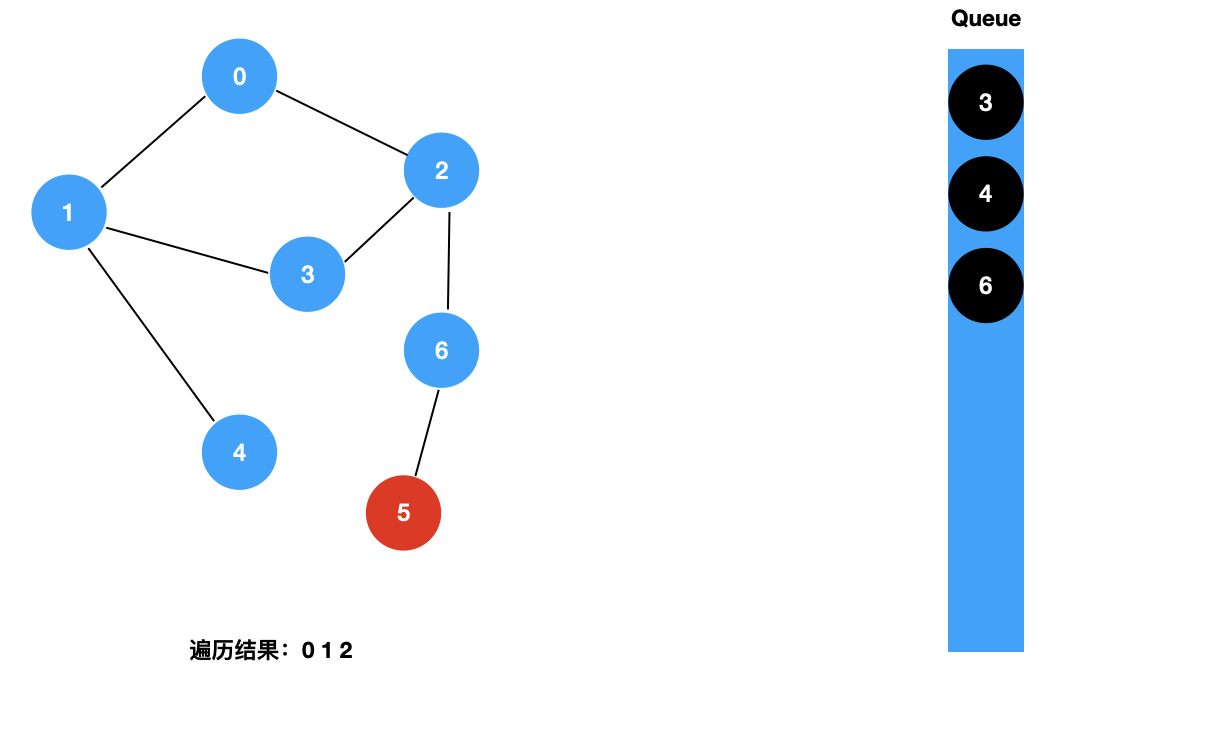
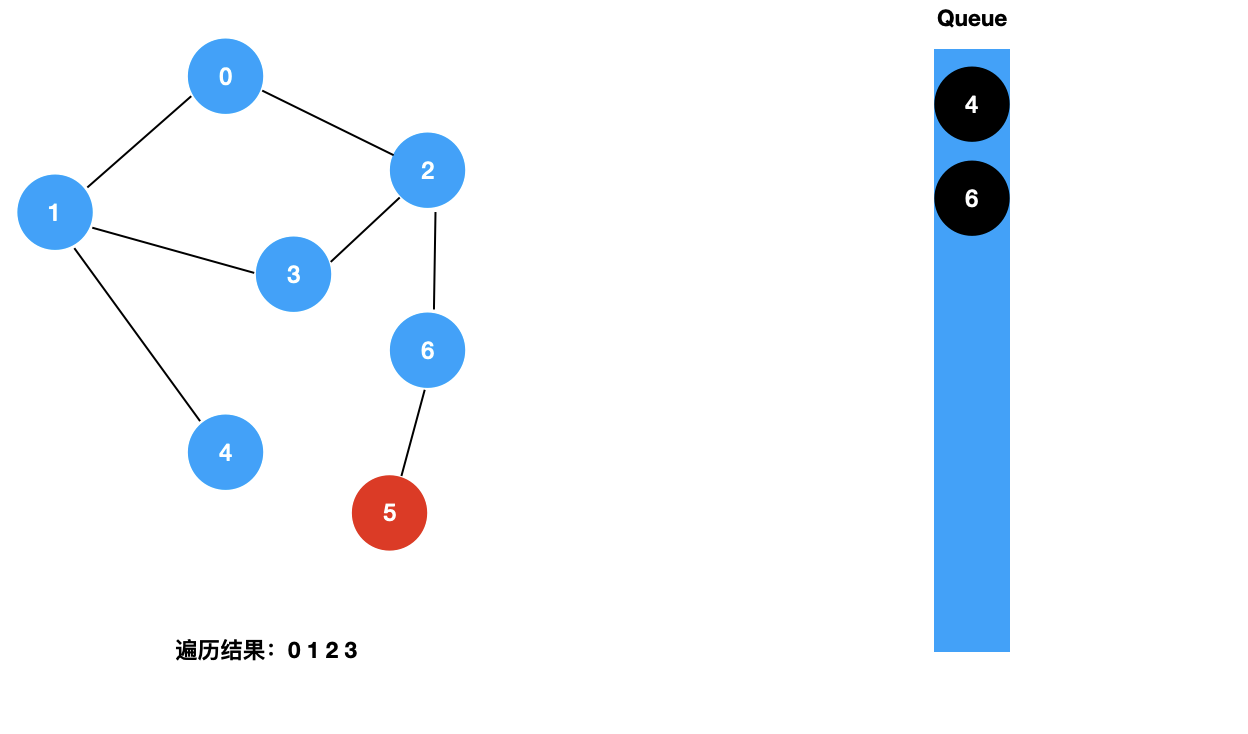
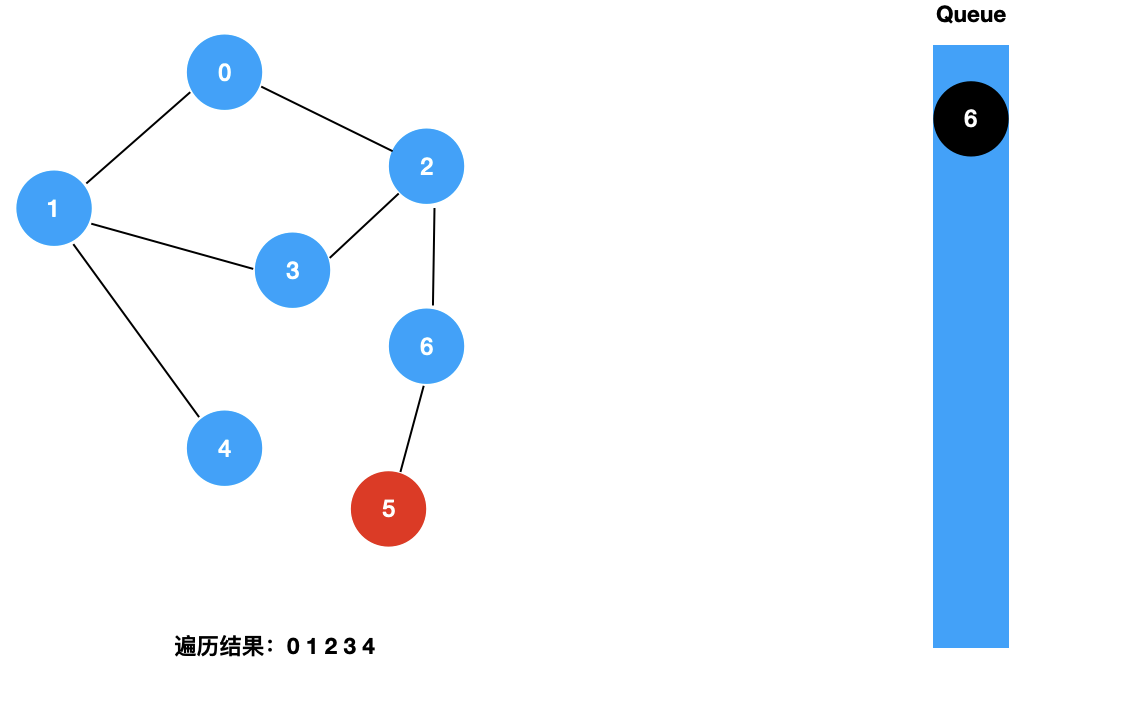
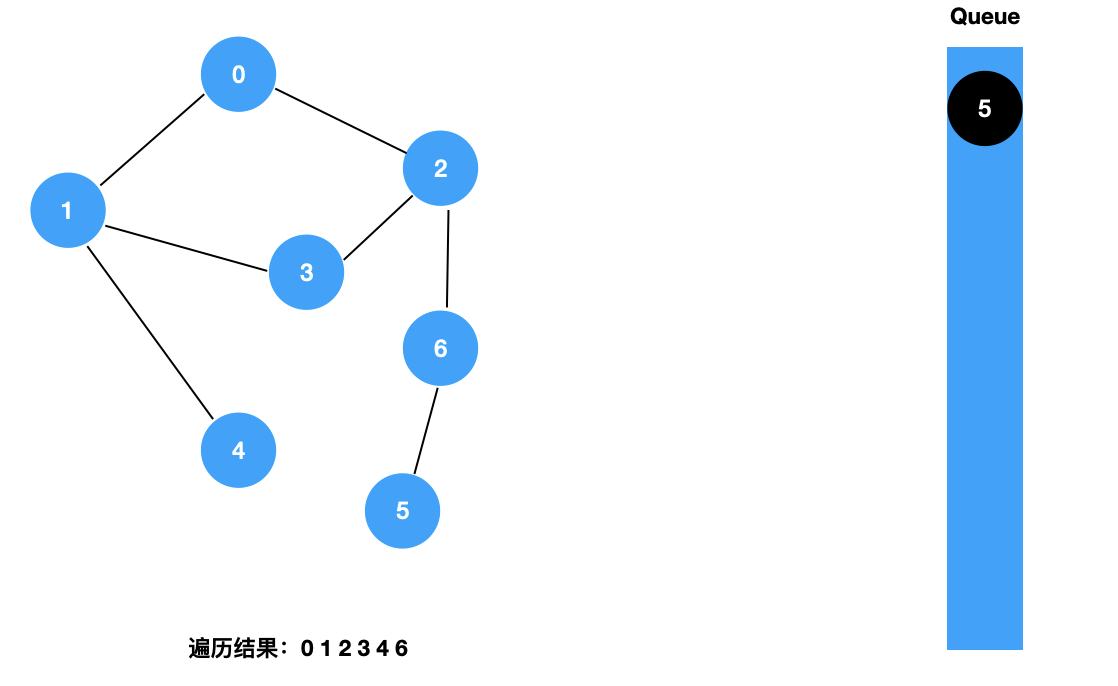
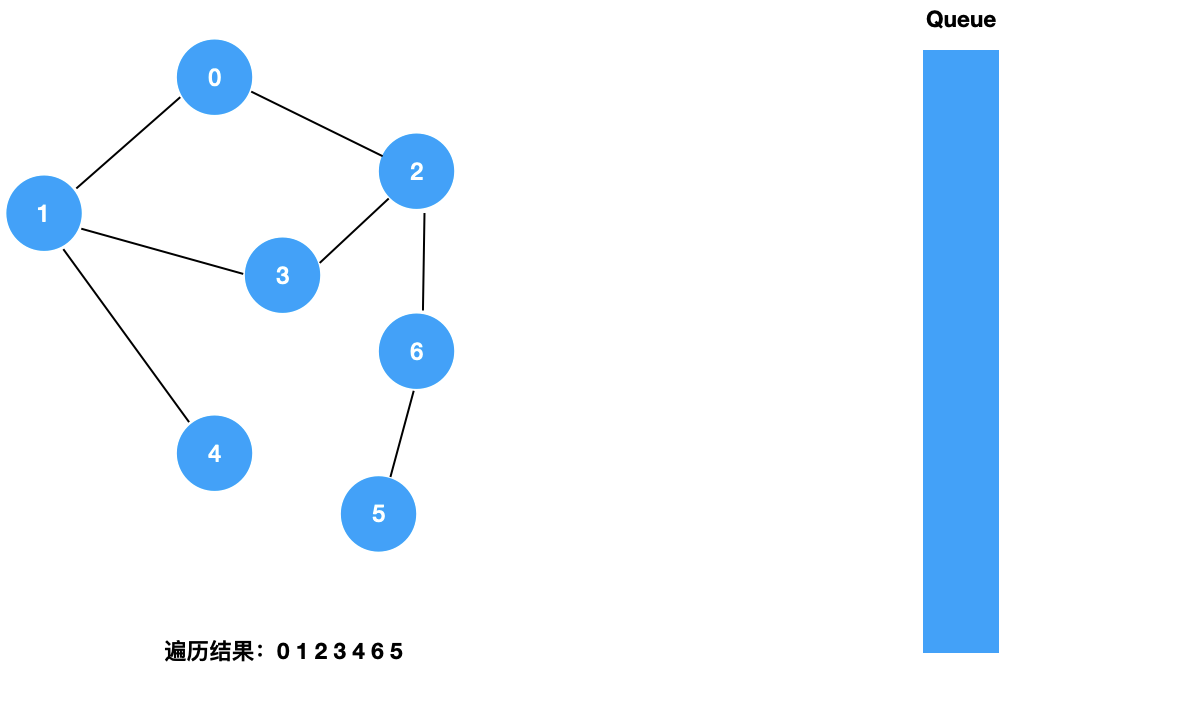
我们来看一下图的广度优先遍历的具体过程：

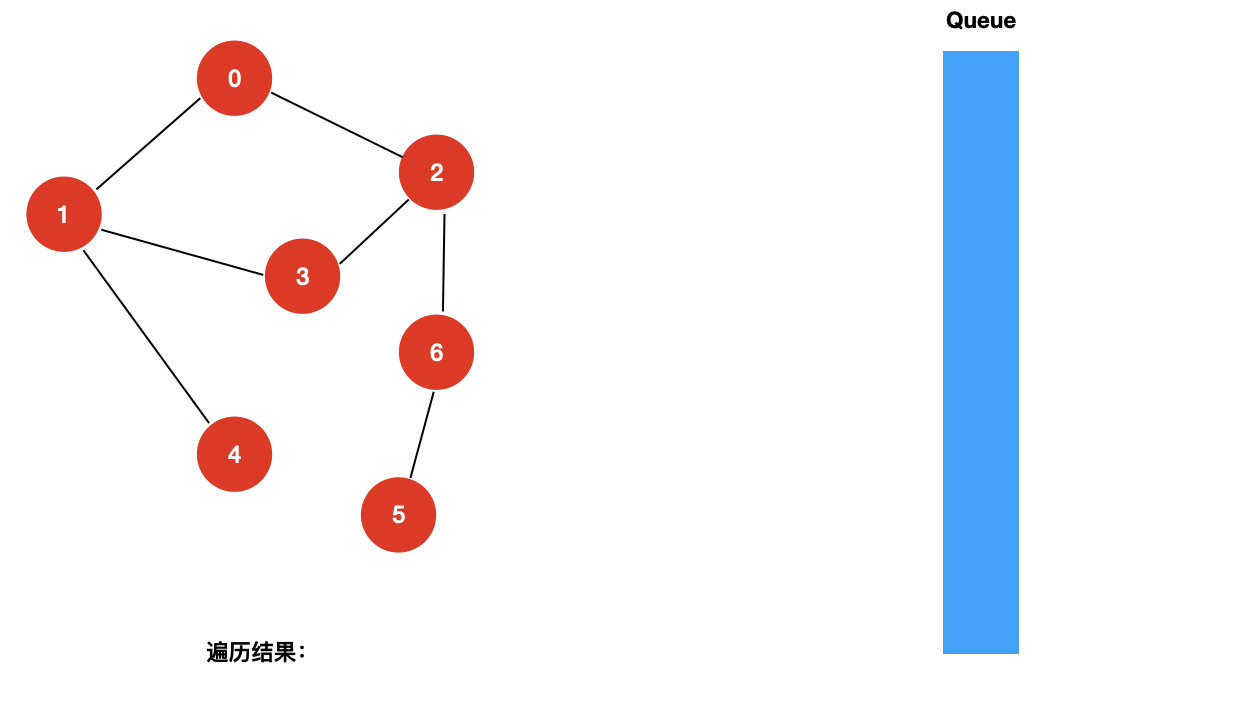
对于上面这样一个图，和树的广度优先遍历一样，我们使用一个辅助的队列，其遍历过程如下所示：

二：图的 BFS 的实现

代码链接🔗

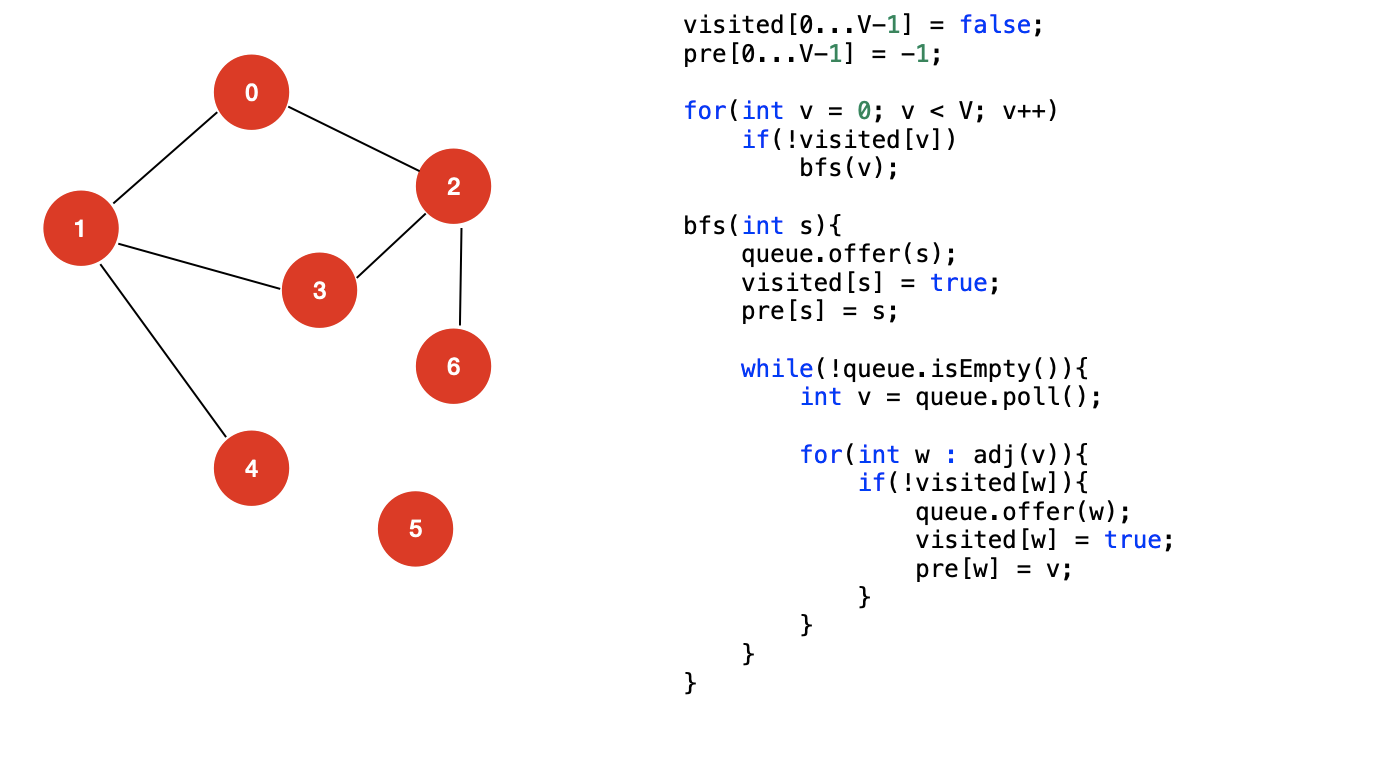
通过上面的过程分析，我们可以轻松地写出图的 BFS 的实现，这里我给出伪代码提供大家参考：

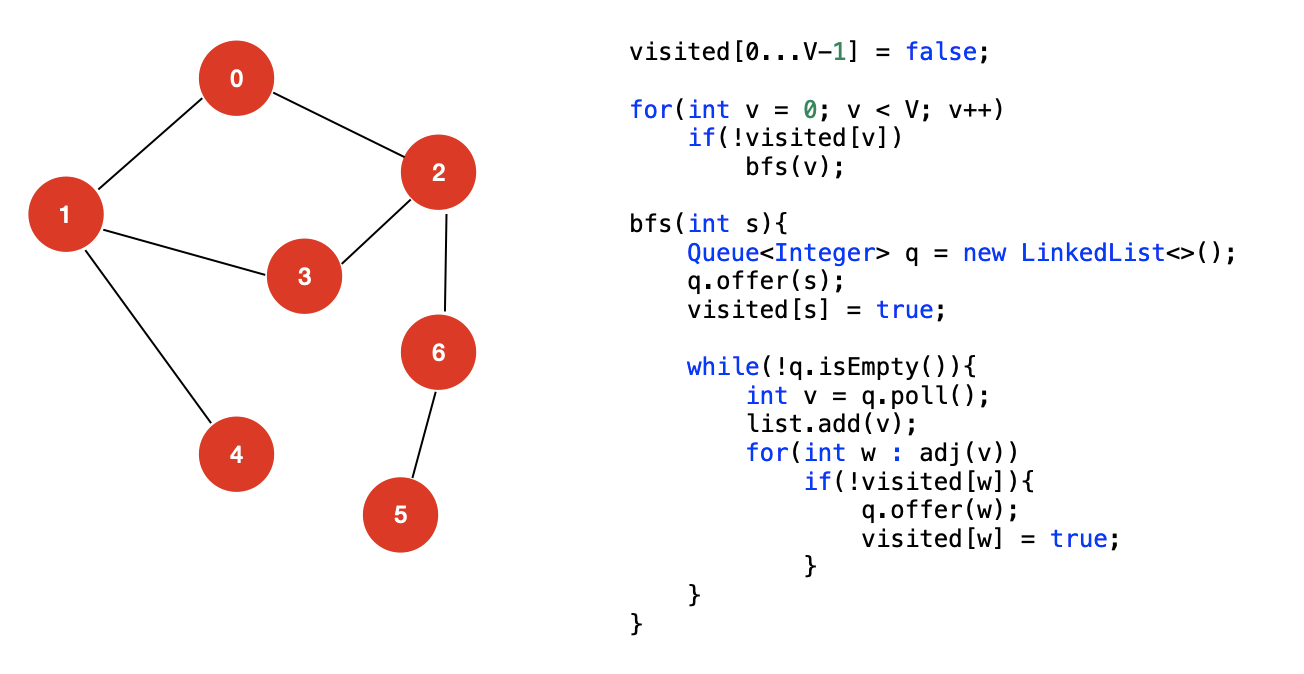
三：使用 BFS 求解路径问题

单源路径问题

代码链接🔗

单源路径问题是指求解从固定的一个顶点 s 到达顶点 t 的一条路径。

对于 DFS 遍历，我们使用了一个数组 pre 来记录顶点 w 是通过遍历顶点 v 而来的，这个信息表示如下：

pre[w] = v;

对于 BFS 遍历实际上是一样的，我们也使用一个数组 pre 用来记录一个顶点是通过遍历哪一个顶点时而来的，然后，将 pre 的信息收集起来即可求解路径。

伪代码如下：

所有点对路径问题

代码链接🔗

和 DFS 实现所有点对路径问题一样，我们只需要将图中的每一个顶点都实现一遍单源路径问题即可，这里就不再赘述了，请点击代码链接进行查看。

路径问题的优化

代码链接🔗

我们在 DFS 求解路径问题时，针对用户只查询一次的情况，单独封装了一个算法类 Path，让用户传入两个点 s 与 t，该算法可以返回从 s 到 t 的一条路径，其优点在于我们不需要去遍历整个图，只要找到了路径，代码可以提前返回。

使用 BFS 算法实现这么一个功能的逻辑实际上是一样，我们也只需要判断，从 s 出发，是否有遍历到点 t，如果遍历到，bfs 方法的逻辑就可以直接返回，伪代码如下所示：

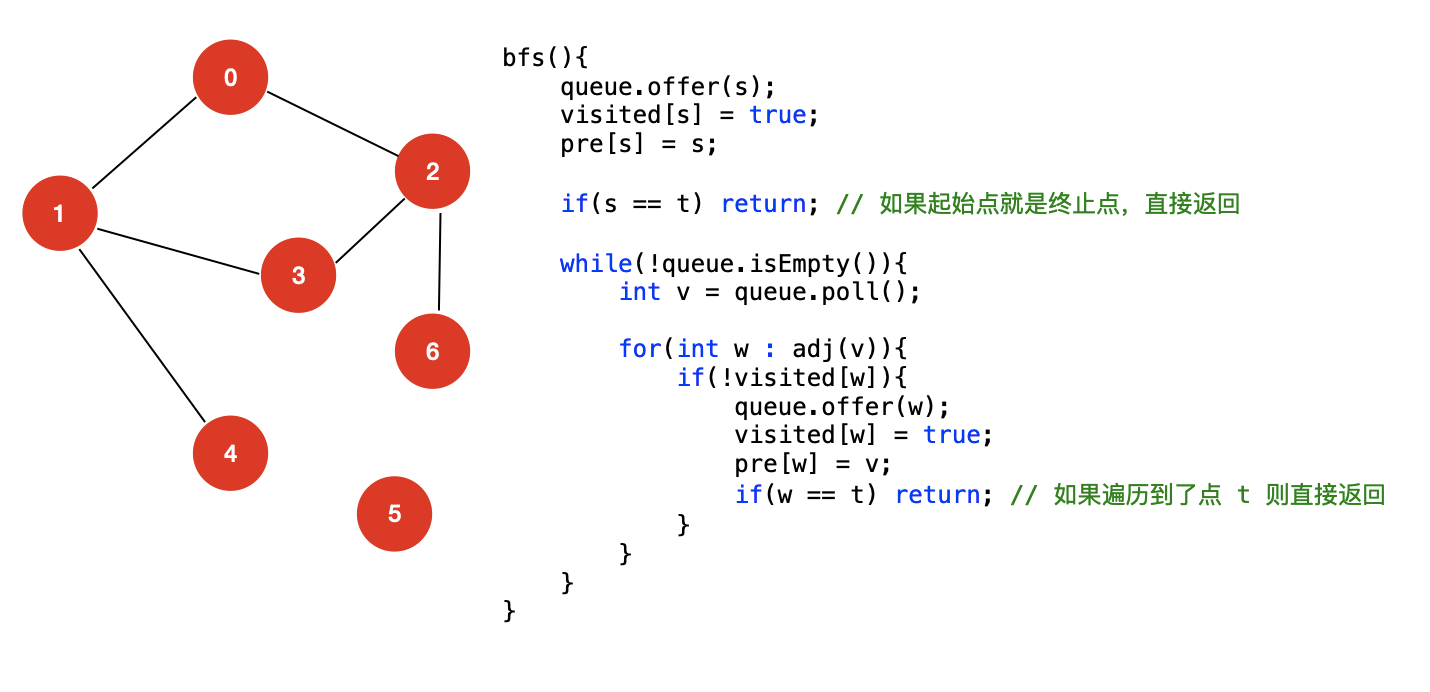
四：使用 BFS 求解联通分量

代码链接🔗

和我们使用 DFS 求解联通分量问题相同，原本我们使用 visited 数组存储布尔值，现在我们使用 visited 数组存储 int 型，存储的值代表同一个联通分量的标志，我们称作为 ccId。详细的代码请点击链接进行查阅，在这里就不再重复赘述了。

五：使用 BFS 求解环检测问题

代码链接🔗

除了 DFS ，BFS 也可以应用到环检测问题。

回顾一下 DFS，在 for(int w : adj(v)) 中，我们判断，当一个顶点 w 已经被访问过，并且 w 还不是 v 的上一个节点时，我们就找到了环。

所以，BFS 是一样的，我们只需要创建一个整型数组 pre 来记录每一个顶点来自于哪一个顶点的遍历，之后，就可以顺利组建我们的逻辑了。

伪代码如下所示：

六：使用 BFS 解决二分图检测

代码链接🔗

我们回顾一下使用 DFS 检测二分图的做法，核心就是在 DFS 过程中对每一个节点进行染色。

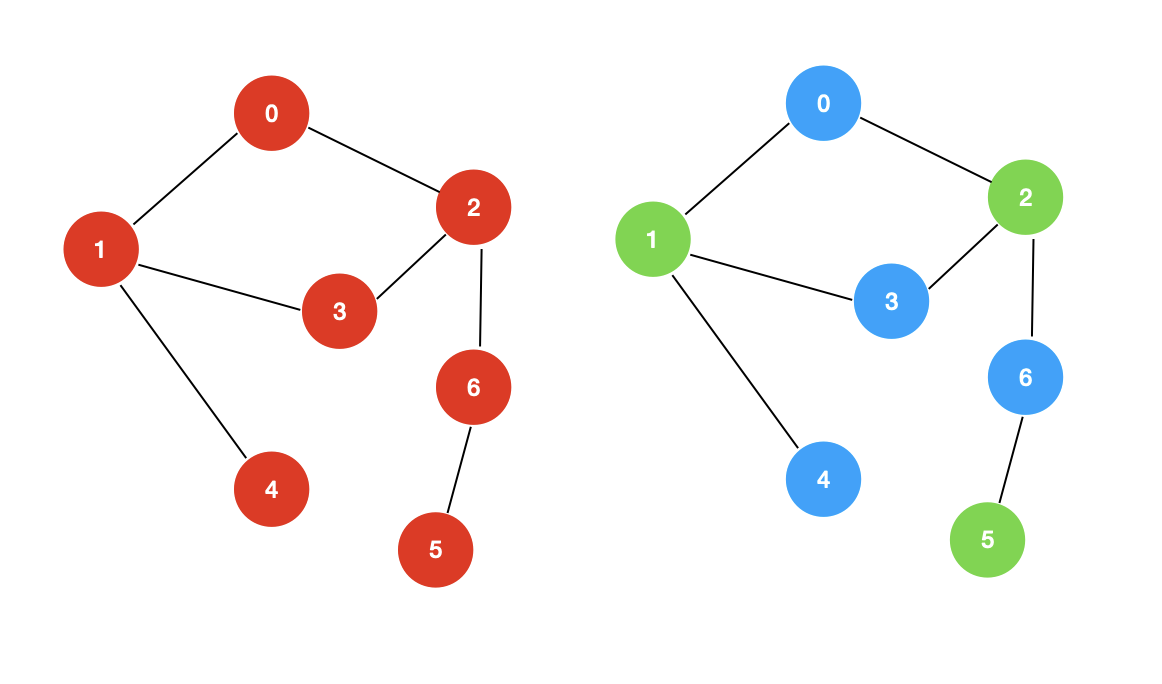
BFS 也是一样的，我们只需要在 BFS 遍历的过程中，对顶点进行“染色”操作，如果染色后，满足二分图的“所有的边的两个端点隶属不同的部分”这个特性，就说明该图是一个二分图。

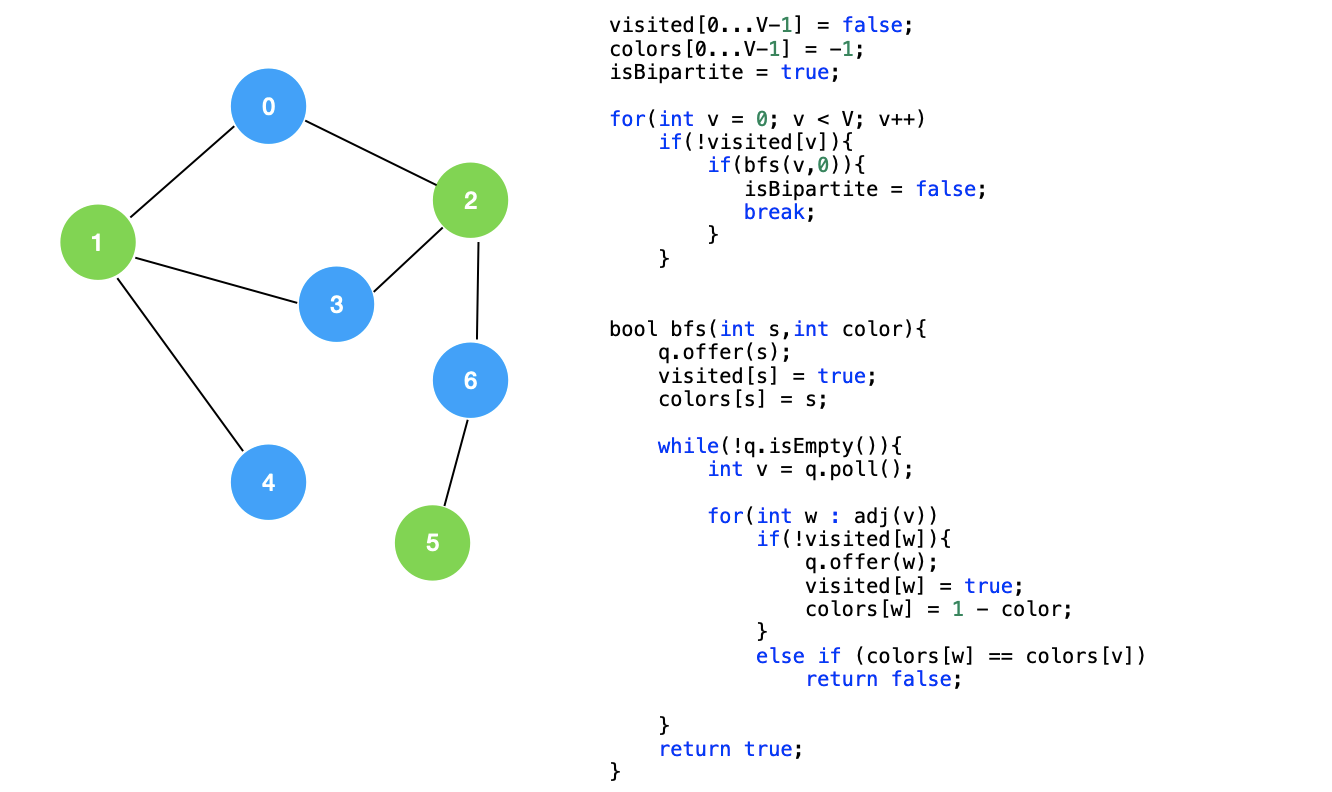
伪代码如下所示：

七：BFS 的重要性质

对于这样的一个图：

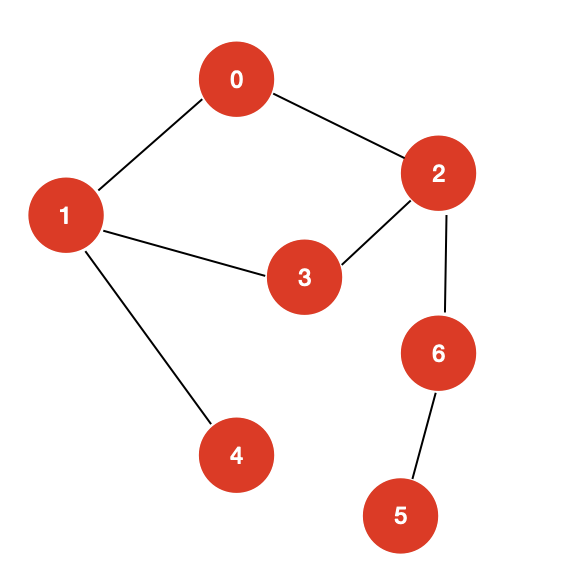
我们使用 DFS 和 BFS 来求解以 0 为源顶点 6 为目标节点的电源路径问题，会有什么样的结果呢？

测试结果如下：

BFS path 0 -> 6 : [0, 2, 6]
DFS path 0 -> 6 : [0, 1, 3, 2, 6]

我们看到，BFS 和 DFS 遍历都可以求解单源路径问题，但是二者的结果是截然不同的。

我们可以发现，BFS 求解的单源路径问题的结果实际上是“最短路径”。

为什么使用 BFS 求解单源路径问题就可以得到最短路径呢？

我们可以先回顾一下树的广度优先遍历：

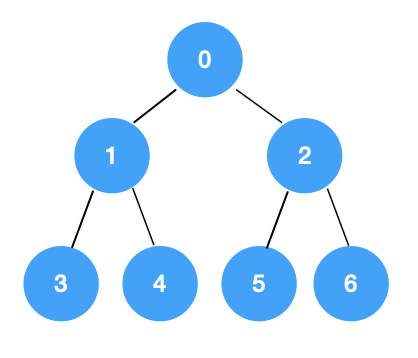
对于树的广度优先遍历，其特点为，后遍历的节点距根节点的距离要大于等于先遍历的节点距根节点的距离。

譬如，节点 6 距根节点 0 的路径距离为 2，节点 3 于节点 6 之前被遍历到，它距根节点 0 的路径也是 2，节点 6 距根节点的距离要大于等于节点 3 距根节点的距离。所以，树的广度优先遍历实际上就是按照距 root 节点的距离进行遍历的。

如果理解了这一点，我们再回到图，就会发现，图和树是一样的，图的广度优先遍历也是按照距源节点的距离遍历所有的顶点：

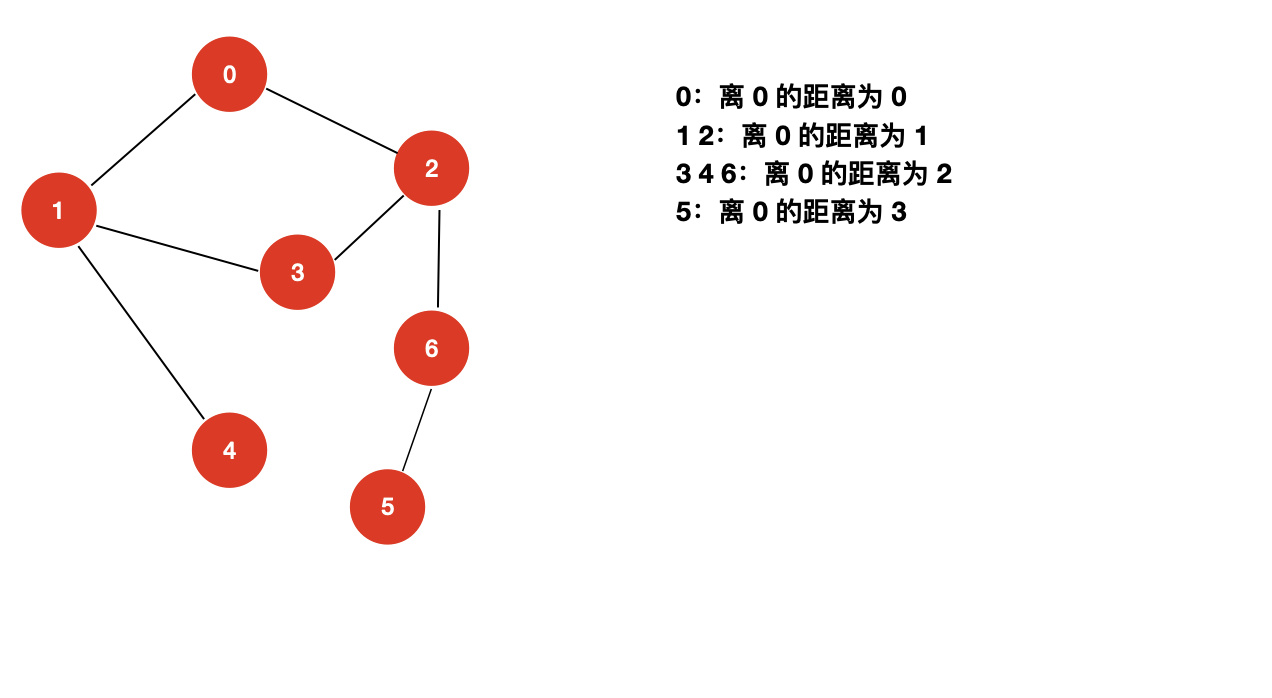
所以，BFS 遍历能够解决 DFS 解决不了的最短路径问题。

八：无权图的最短路径

代码链接🔗

我们已经知道 BFS 可以求解最短路径问题，那么我们如何获取从一个源顶点到目标顶点的距离是多少呢？其实非常简单，我们只需要在 BFS 遍历的过程中多维护一个数组 dis 即可，dis 数组用来保存从源节点出发到各个节点的距离值。

伪代码如下：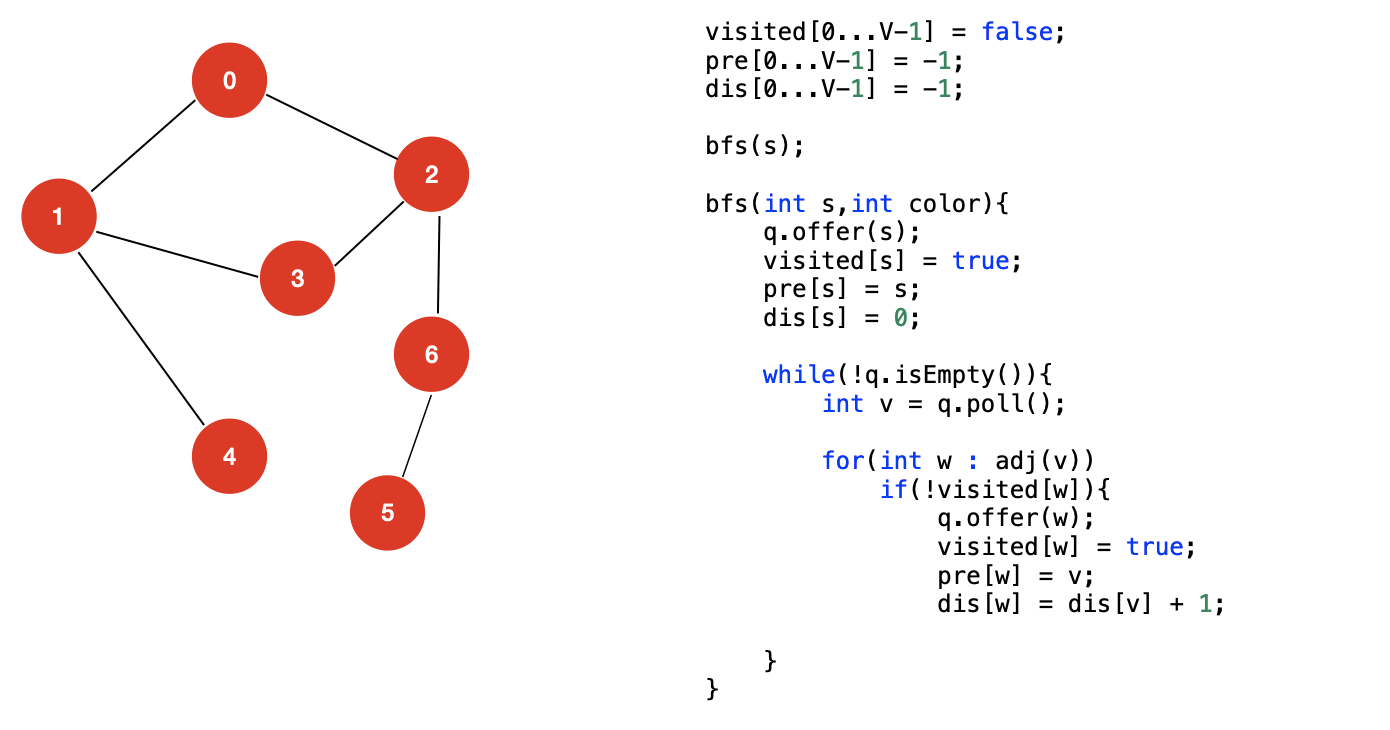

我们已经知道 BFS 可以求解单源路径问题，那么，所有点对最短路径以及任意两点的最短路径问题也就迎刃而解了。在这里，我给出任意两点的最短路径问题的代码，就不再赘述逻辑了，大家可以点击下方链接进行查看：

代码链接🔗

九：DFS 和 BFS 的联系

当我们将 DFS 转换为非递归写法时，我们发现 DFS 和 BFS 的本质其实就是 DFS 使用了栈这种数据结构，而 BFS 使用了队列这种数据结构。
也就是说，DFS 和 BFS 的逻辑实际上是一致的，他们的不同只是在于选择的“容器”的不同。