0 题目来源

acwing

1 涉及到的知识点

递归、全排列等

1.1 给定位数范围的全排列模板

vector<int> vec;
int test[10];
void dfs(int u)
{
    if (u > 3)//位数范围为1~3位
        return;
    for (int i = 0; i < vec.size(); i++)
        cout << vec[i] << ' ';
    cout << endl;
    for (int i = 1; i <= 9; i++)//1~9的数字
    {
        if (test[i] == 0)
        {
            test[i] = 1;
            vec.push_back(i);
            dfs(u + 1);
            vec.pop_back();
            test[i] = 0;
        }
    }
}

1.2 确定位数的全排列模板

vector<int> vec;
int test[10];
void dfs(int u)
{
    if (u == 3)//确定输出3位
    {
        for (int i = 0; i < vec.size(); i++)
            cout << vec[i] << ' ';
        cout << endl;
        return;
    }
    for (int i = 1; i <= 9; i++)//1~9的数字
    {
        if (test[i] == 0)
        {
            test[i] = 1;
            vec.push_back(i);
            dfs(u + 1);
            vec.pop_back();
            test[i] = 0;
        }
    }
}

1.3 逐位取出一个整数中的每一位模板

while (num)
{
    int temp = num % 10;//temp即为每一位
    b /= 10;
}

2 题目描述

100可以表示为带分数的形式：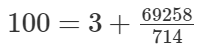
还可以表示为：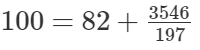
注意特征：带分数中，数字1∼9分别出现且只出现一次（不包含0）。
类似这样的带分数，100有11种表示法。

3 输入输出

输入格式：
一个正整数。
输出格式：
输出输入数字用数码1∼9不重复不遗漏地组成带分数表示的全部种数。
数据范围：

4 样例

输入样例1：
100
输出样例1：
11
输入样例2：
105
输出样例2：
6

5 思路

本题需要分别取a、b、c，使其满足。
上式可以变形为
因此，只要确定a、c，则b可以计算得出。
因此，可以通过两个嵌套的全排列（给定位数范围），对a、c的所有可能情况进行枚举，并计算相应的b，检测满足题意的情况个数，即得到答案。

6 代码

#include<iostream>
#include<cstring>
long long ans, n;
int test[10];
int cpytest[10];
using namespace std;
bool check(long long b)
{
    memcpy(cpytest, test, sizeof test);//容易遗漏，由于需要多次检测，而每次检测会对检测数组进行改变，因此在每次检测开始前需要对检测数组进行还原。
    while (b)
    {
        int temp = b % 10;
        b /= 10;
        if (temp == 0)
            return false;
        if (cpytest[temp] == 0)
            cpytest[temp] = 1;
        else
            return false;
    }
    for (int i = 1; i <= 9; i++)//容易遗漏，遍历cpytest，确保a、b、c覆盖1~9所有位
    {
        if (cpytest[i] == 0)
            return false;
    }
    return true;
}
void dfs_c(int u, long long a, long long c)
{
    if (u > 9)
        return;
    long long b = n * (long long)c - a * c;
    if (a != 0 && c != 0 && b != 0 && check(b))
        ans++;
    for (int i = 1; i <= 9; i++)
    {
        if (test[i] == 0)
        {
            test[i] = 1;
            dfs_c(u + 1, a, c * 10 + i);
            test[i] = 0;
        }
    }
}
void dfs_a(int u, long long a)
{
    if (a >= n)
        return;
    if(a)
        dfs_c(u, a, 0);
    for (int i = 1; i <= 9; i++)
    {
        if (test[i] == 0)
        {
            test[i] = 1;
            dfs_a(u + 1, a * 10 + i);
            test[i] = 0;
        }
    }
}
int main()
{
    cin >> n;
    dfs_a(0, 0);
    cout << ans;
    return 0;
}