0 题目来源

力扣《程序员面试金典》

1 涉及到的知识点

矩阵、数组

2 题目描述

给你一幅由 N × N 矩阵表示的图像，其中每个像素的大小为 4 字节。请你设计一种算法，将图像旋转 90 度。
不占用额外内存空间能否做到？

3 样例

示例 1:
给定 matrix =
[
[1,2,3],
[4,5,6],
[7,8,9]
],
原地旋转输入矩阵，使其变为:
[
[7,4,1],
[8,5,2],
[9,6,3]
]
示例 2:
给定 matrix =
[
[ 5, 1, 9,11],
[ 2, 4, 8,10],
[13, 3, 6, 7],
[15,14,12,16]
],
原地旋转输入矩阵，使其变为:
[
[15,13, 2, 5],
[14, 3, 4, 1],
[12, 6, 8, 9],
[16, 7,10,11]
]

4 思路

4.1 方法一：逐层逐个交换

本题要求不要占用额外的矩阵空间，因此可以想到采用交换元素的方法。
为了减小时间复杂度，因此采用逐层遍历的方法。
交换方法如下：（圈内和圈内的交换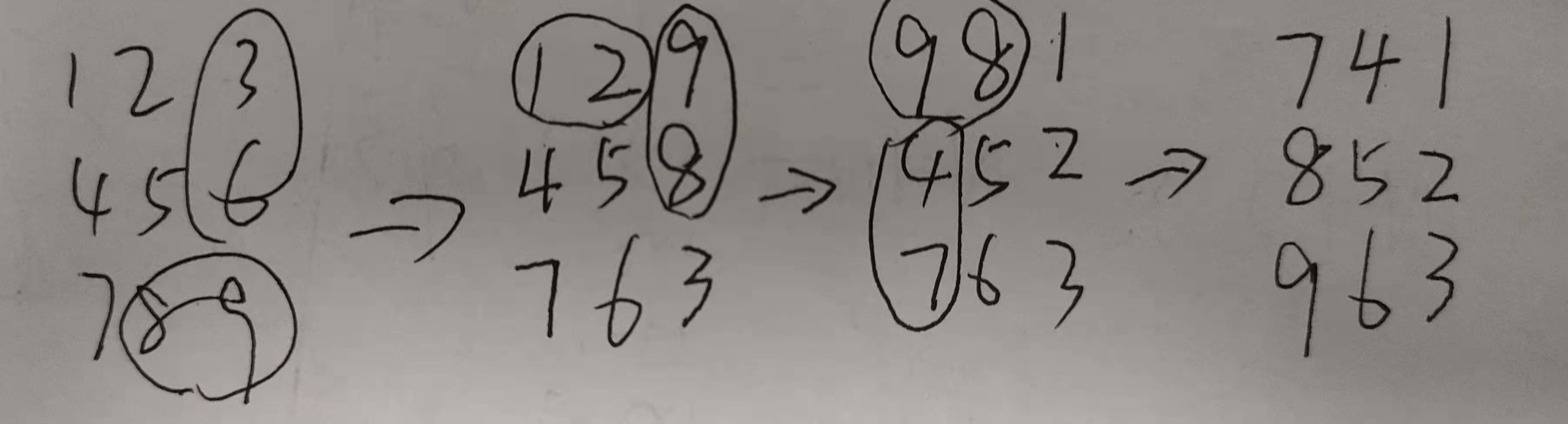）c58bd8cc123cd86de8b2871babf990e.jpg
每个矩阵共有旋转矩阵 - 图2（向下取整）层（N为行/列数），每层都以此类推，每部分元素交换3次。

该方法难点在于每个元素坐标的计算和表示，需花费较多时间推导。 关键等式为：matrix[row][col]=matrix[n−col−1][row]

4.2 方法二：翻转矩阵

先将矩阵水平翻转90度，然后再沿着对角线翻转一次，就可以得到旋转90度的矩阵。
点击查看：力扣的官方题解解释

5 代码

5.1 方法一

  1. class Solution {
  2. public:
  3.     void rotate(vector<vector<int>>& matrix) {
  4.         int N=matrix.size();
  5.         for(int i=0;i<N/2;i++)//遍历层数
  6.         {
  7.             for(int j=i+1;j<N-i;j++)
  8.             {
  9.                 swap(matrix[N-1-i][j],matrix[N-1-j][N-1-i]);
  10.                 swap(matrix[N-1-j][N-1-i],matrix[i][N-1-j]);
  11.                 swap(matrix[i][N-1-j],matrix[j][i]);
  12.             }
  13.         }
  14.     }
  15. };

5.2 方法2

  1. class Solution {
  2. public:
  3.     void rotate(vector<vector<int>>& matrix) {
  4.         int n = matrix.size();
  5.         // 水平翻转
  6.         for (int i = 0; i < n / 2; ++i) {
  7.             for (int j = 0; j < n; ++j) {
  8.                 swap(matrix[i][j], matrix[n - i - 1][j]);
  9.             }
  10.         }
  11.         // 主对角线翻转
  12.         for (int i = 0; i < n; ++i) {
  13.             for (int j = 0; j < i; ++j) {
  14.                 swap(matrix[i][j], matrix[j][i]);
  15.             }
  16.         }
  17.     }
  18. };
  19. /*本方法来自力扣官方题解*/