本题来自于《算法设计与分析》课程实验的计蒜客题目，未经授权请勿转载

1 本题涉及到的知识点

树的先序遍历、图的邻接表

2 题目描述

在蒜头君的国度里有个城市，这个城市间只有条路把这个个城市连接起来。现在，蒜头君在第号城市，他有张该国地图，他想知道如果自己要去参观第号城市，必须经过的前一个城市是几号城市（假设你不走重复的路）。

3 输入与输出格式

3.1 输入格式

第一行输入一个整数表示测试数据共有 #card=math&code=M%281%5Cle%20M%5Cle%205%29&id=EqXS7)组。
每组测试数据的第一行输入一个正整数#card=math&code=N%281%5Cle%20N%5Cle%20100000%29&id=i7wWd)和一个正整数#card=math&code=S%281%5Cle%20S%5Cle%20N%29&id=dvHtw)，表示城市的总个数，表示蒜头君所在城市的编号。
随后的行，每行有两个正整数#card=math&code=a%2Cb%281%5Cle%20a%2Cb%5Cle%20N%29&id=HUFeg)，表示第号城市和第号城市之间有一条路连通。

3.2 输出格式

每组测试数据输个正整数，其中，第个数表示从走到号城市，必须要经过的上一个城市的编号。（其中时，请输出）。

4 样例

4.1 样例输入

1 
10 1 
1 9 
1 8 
8 10 
10 3 
8 6 
1 2 
10 4 
9 5 
3 7

4.2 样例输出

-1 1 10 10 9 8 3 1 1 8

5 分析

5.1 问题的转化

本题目提到个城市间只有条路把这个个城市连接起来，因此整个地图将构成树，蒜头君所在的城市即为树的根节点。要前往一个城市，必须要经过的城市就是这个城市的父节点。因此，问题转化为：已知一颗树，如何能求出每个结点的父结点？

5.2 求父节点的方法

我们可以使用树的先序遍历对整个树进行遍历，在这个过程中对所有结点的父结点进行记录，从而得出问题的答案。

5.3 树的存储方法

由于本题在输入树的时候，还不知道根结点与其他结点的连接关系，因此只能采用无向图的存储方式来存储，可选的方式为邻接矩阵或者邻接表。
由于本题数据规模较大：#card=math&code=N%281%5Cle%20N%5Cle%20100000%29&id=QwSdo)，使用邻接矩阵存储很可能会导致空间超限。因此，使用邻接表的方式最为合适，我们在这里使用vector数组来作为邻接表，记录每个结点相连接的其他所有结点的序号：vector<int> t[100001]。

5.4 避免重复访问的方法

由于我们在存储树的时候，是按照无向图的方式来存储，并不是只存储了该结点的子结点，而是把所有具有连接关系的结点都进行了存储。所以，如果直接进行先序遍历的话，会导致重复访问节点（A访问B，B访问A……以此循环），出现死循环。因此，我们需要用visit数组来记录是否访问过了某个结点，如果访问过了，则不对它进行遍历。

6 源代码

#include<iostream>
#include<vector>
using namespace std;
int father[100001];
void travel(int head, int lasthead, vector<int>* t, int* visit)
/*函数功能：递归形式的树的先序遍历，在遍历途中，把每个结点的父节点记录到father数组中。
四个参数的含义：
head：当前正在遍历的结点序号
lasthead：当前正在遍历的结点的父节点序号
t：被遍历的树（vector数组，记录了相邻两个结点的连接关系）
visit：避免重复访问而设置的数组。由于vector数组t记录的连接关系的双向的，因此，为了避免重复访问，需要使用visit数组检测该结点是否已经遍历过了。
*/
{
    father[head] = lasthead;//设置当前结点的父节点是lasthead
    visit[head] = 1;//表示该结点已经访问过了
    for (int i = 0; i < t[head].size(); i++)//遍历所有与当前结点连接的结点
    {
        if (!visit[t[head][i]])//如果这个结点还没有被访问过
            travel(t[head][i], head, t, visit);//使用先序遍历对其进行访问
    }
}
int main()
{
    int m;
    cin >> m;//输入测试数据的个数
    for (int i = 0; i < m; i++)//遍历每次的测试数据
    {
        int n, s;
        cin >> n >> s;//输入城市个数、蒜头君在哪个城市
        father[s] = -1;//定义蒜头君所在城市的父结点为-1（无父节点）
        int visit[100001] = { 0 };//清除访问过的城市
        vector<int> t[100001];//定义树vector数组
        for (int j = 0; j < n - 1; j++)//输入n-1组数据
        {
            int a, b;
            cin >> a >> b;//输入连接的两个结点号
            t[a].push_back(b);//把相应结点号加入到对应vector结点中
            t[b].push_back(a);//表示a与b连接，b也与a连接
        }
        travel(s, -1, t, visit);//对该树进行先序遍历，遍历途中记录每个结点的父节点，存到father数组中。这里传入-1参数的原因是，根节点的父结点为-1
        for (int j = 1; j <= n; j++)//遍历father数组
            cout << father[j]<<" ";//打印输出每个结点的父节点
    }
}

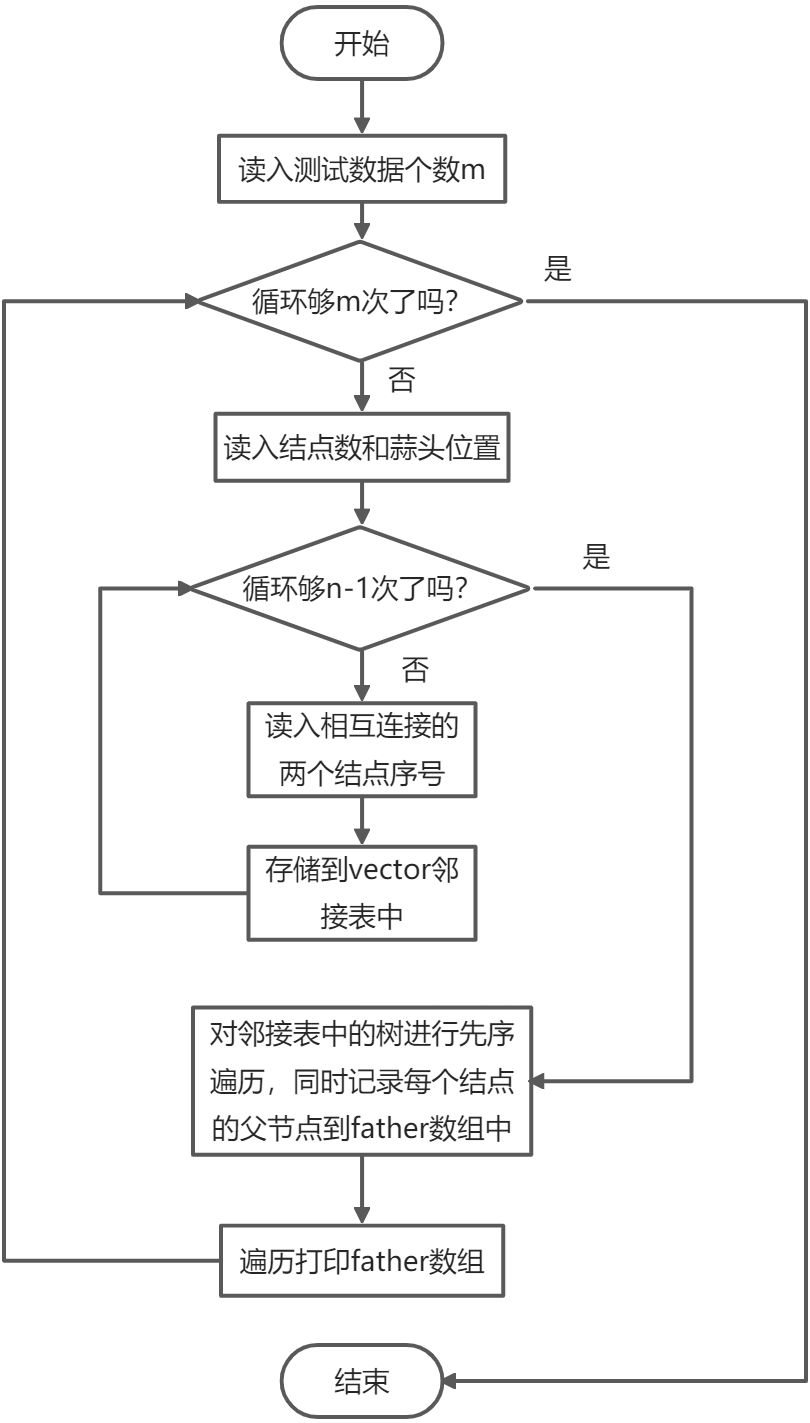
7 主函数流程图