0 题目来源

acwing

1 涉及的知识点

位运算、地图的坐标、增量数组、memcpy

位运算
对于需要对每一位进行二元遍历的情况，可以使用位运算+for循环进行简单遍历：
如要求对2位进行0/1遍历，则需要遍历数字0~3

  1. 0——00
  2. 1——01
  3. 2——10
  4. 3——11

可以使用num>>i&1（num为遍历数字，i为待取出的位数）来取出相应位置的数字。

地图的坐标
通常采用如下方式对地图建立坐标系：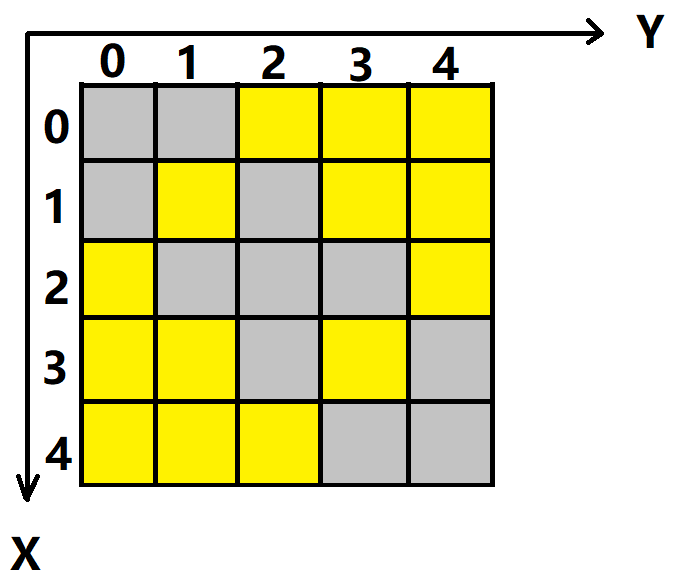
image.png

增量数组
为了方便对一个坐标的上下左右元素进行遍历，可以定义增量数组，如下：

  1. int incx[5] = { -1,1,0,0,0 };//定义增量数组
  2. int incy[5] = { 0,0,-1,1,0 };//上下左右中

memcpy函数
见如下文章：
0 常用基础知识点总结

2 题目描述

你玩过“拉灯”游戏吗？
2525 盏灯排成一个 5×55×5 的方形。
每一个灯都有一个开关，游戏者可以改变它的状态。
每一步，游戏者可以改变某一个灯的状态。
游戏者改变一个灯的状态会产生连锁反应：和这个灯上下左右相邻的灯也要相应地改变其状态。
我们用数字 11 表示一盏开着的灯，用数字 00 表示关着的灯。
下面这种状态
10111
01101
10111
10000
11011
在改变了最左上角的灯的状态后将变成：
01111
11101
10111
10000
11011
再改变它正中间的灯后状态将变成：
01111
11001
11001
10100
11011
给定一些游戏的初始状态，编写程序判断游戏者是否可能在 66 步以内使所有的灯都变亮。

3 输出输出

输入格式
第一行输入正整数 nn，代表数据中共有 nn 个待解决的游戏初始状态。
以下若干行数据分为 nn 组，每组数据有 55 行，每行 55 个字符。
每组数据描述了一个游戏的初始状态。
各组数据间用一个空行分隔。
输出格式
一共输出 nn 行数据，每行有一个小于等于 66 的整数，它表示对于输入数据中对应的游戏状态最少需要几步才能使所有灯变亮。
对于某一个游戏初始状态，若 66 步以内无法使所有灯变亮，则输出 −1−1。
数据范围
0

4 样例

输入样例：
3
00111
01011
10001
11010
11100

11101
11101
11110
11111
11111

01111
11111
11111
11111
11111
输出样例：
3
2
-1

5 思路

本题为固定的5x5地图，例如一个5x5地图如下：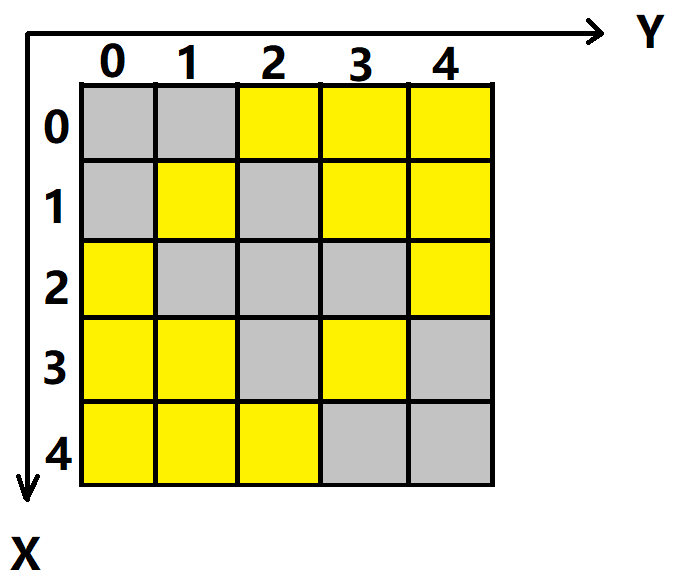
image.png
通过按下第二行的(1,0)和(1,1)，可以使第一行全部变亮。
同理，在第二行按完后，通过按下第三行的相应位置（第二行暗色的下面相应位置），也可以使得第二行全部变亮。以此类推，可以使得所有色块均变亮。
于是，对于第一行的每一种情况，在后面4行都有着唯一确定的按法，因此，我们只需要遍历第一行的所有情况，尝试按下后面四行，记录最小步数，则该最小步数为最终答案。如果最后一行也已按完，但最后一行仍有未亮起的色块，则说明本方案无解。
对第一行的5个色块进行按下/不按下的遍历，共有2^5=32种情况，这里我们可以使用位运算的方法对其进行遍历：
遍历数字0~31，对每个数字，都有一个唯一的5位二进制数字与其对应，代表着第一行每一位的按下情况，为1则按下，为0则不按。
取出5位二进制数中一位的方法：

  1. for(int num=0;num<32;num++)//遍历0~31
  2.     for(int i=0;i<5;i++)
  3.         num>>i&1;//将当前数字的二进制形式向右移动i位，与1相与，即取出该位的数字

注意事项：

  • 使用增量数组，从而方便地遍历坐标上下左右的位置。

    6 代码

    1. #include<iostream>
    2. #include<cstring>
    3. #define INF 233333333
    4. using namespace std;
    5. char mp[6][6];
    6. int incx[5] = { -1,1,0,0,0 };//定义增量数组
    7. int incy[5] = { 0,0,-1,1,0 };
    8. void turn(int x, int y)
    9. {
    10.   for (int i = 0; i < 5; i++)
    11.   {
    12.       if (x + incx[i] >= 0 && y + incy[i] >= 0)
    13.       {
    14.           if (mp[x + incx[i]][y + incy[i]] == '1')
    15.               mp[x + incx[i]][y + incy[i]] = '0';
    16.           else
    17.               mp[x + incx[i]][y + incy[i]] = '1';
    18.       }
    19.   }
    20. }
    21. int main()
    22. {
    23.   int n;
    24.   cin >> n;
    25.   for (int i = 0; i < n; i++)
    26.   {
    27.       char tempmp[6][6];
    28.       for (int j = 0; j < 5; j++)
    29.           for (int k = 0; k < 5; k++)
    30.               cin >> tempmp[j][k];
    31.       int mintimes = INF;//记录最小步数
    32.       for (int op = 0; op < 32; op++)//遍历第0行的状态
    33.       {
    34.           int times = 0;//记录当前步数
    35.           memcpy(mp, tempmp, sizeof(mp));
    36.           for (int j = 0; j < 5; j++)//取出op的每一位
    37.           {
    38.               if (op >> j & 1)//如果该位为1，表示按下
    39.               {
    40.                   turn(0, j);
    41.                   times++;
    42.               }
    43.           }
    44.           for (int j = 1; j < 5; j++)//遍历第1~4行（从0开始数）
    45.           {
    46.               for (int k = 0; k < 5; k++)//遍历第0~4列
    47.               {
    48.                   if (mp[j - 1][k] == '0')
    49.                   {
    50.                       turn(j, k);
    51.                       times++;
    52.                   }
    53.               }
    54.           }
    55.           int suc = 1;//记录是否成功
    56.           for (int j = 0; j < 5; j++)
    57.           {
    58.               if (mp[4][j] == '0')//如果最后一行有一个为0
    59.               {
    60.                   suc = 0;//失败
    61.                   break;
    62.               }
    63.           }
    64.           if (suc && (times < mintimes))
    65.               mintimes = times;//如果当前步数小于最小步数，更新mintimes
    66.       }
    67.       if (mintimes == INF || mintimes > 6)//如果最小步数小于6，则说明失败
    68.           cout << -1 << endl;
    69.       else
    70.           cout << mintimes << endl;
    71.   }
    72.   return 0;
    73. }