详解ROIAlign的基本原理和实现细节

剪辑自：http://blog.leanote.com/post/afanti/b5f4f526490b

ROI Align 是在Mask-RCNN这篇论文里提出的一种区域特征聚集方式, 很好地解决了ROI Pooling操作中两次量化造成的区域不匹配(mis-alignment)的问题。实验显示，在检测测任务中将 ROI Pooling 替换为 ROI Align 可以提升检测模型的准确性。

1. ROI Pooling 的局限性分析

在常见的两级检测框架（比如Fast-RCNN，Faster-RCNN，RFCN）中，ROI Pooling 的作用是根据预选框的位置坐标在特征图中将相应区域池化为固定尺寸的特征图，以便进行后续的分类和包围框回归操作。由于预选框的位置通常是由模型回归得到的，一般来讲是浮点数，而池化后的特征图要求尺寸固定。故ROI Pooling这一操作存在两次量化的过程。

• 将候选框边界量化为整数点坐标值。
• 将量化后的边界区域平均分割成 k x k 个单元(bin),对每一个单元的边界进行量化。

事实上，经过上述两次量化，此时的候选框已经和最开始回归出来的位置有一定的偏差，这个偏差会影响检测或者分割的准确度。在论文里，作者把它总结为“不匹配问题（misalignment）。

下面我们用直观的例子具体分析一下上述区域不匹配问题。如 图1 所示，这是一个Faster-RCNN检测框架。输入一张800800的图片，图片上有一个665665的包围框(框着一只狗)。图片经过主干网络提取特征后，特征图缩放步长（stride）为32。因此，图像和包围框的边长都是输入时的1/32。800正好可以被32整除变为25。但665除以32以后得到20.78，带有小数，于是ROI Pooling 直接将它量化成20。接下来需要把框内的特征池化77的大小，因此将上述包围框平均分割成77个矩形区域。显然，每个矩形区域的边长为2.86，又含有小数。于是ROI Pooling 再次把它量化到2。经过这两次量化，候选区域已经出现了较明显的偏差（如图中绿色部分所示）。更重要的是，该层特征图上0.1个像素的偏差，缩放到原图就是3.2个像素。那么0.8的偏差，在原图上就是接近30个像素点的差别，这一差别不容小觑。

图 1

2. ROI Align 的主要思想和具体方法

为了解决ROI Pooling的上述缺点，作者提出了ROI Align这一改进的方法(如图2)。ROI Align的思路很简单：取消量化操作，使用双线性内插的方法获得坐标为浮点数的像素点上的图像数值,从而将整个特征聚集过程转化为一个连续的操作，。值得注意的是，在具体的算法操作上，ROI Align并不是简单地补充出候选区域边界上的坐标点，然后将这些坐标点进行池化，而是重新设计了一套比较优雅的流程，如 图3 所示：

• 遍历每一个候选区域，保持浮点数边界不做量化。
• 将候选区域分割成k x k个单元，每个单元的边界也不做量化。
• 在每个单元中计算固定四个坐标位置，用双线性内插的方法计算出这四个位置的值，然后进行最大池化操作。

这里对上述步骤的第三点作一些说明：这个固定位置是指在每一个矩形单元（bin）中按照固定规则确定的位置。比如，如果采样点数是1，那么就是这个单元的中心点。如果采样点数是4，那么就是把这个单元平均分割成四个小方块以后它们分别的中心点。显然这些采样点的坐标通常是浮点数，所以需要使用插值的方法得到它的像素值。在相关实验中，作者发现将采样点设为4会获得最佳性能，甚至直接设为1在性能上也相差无几。事实上，ROI Align 在遍历取样点的数量上没有ROIPooling那么多，但却可以获得更好的性能，这主要归功于解决了misalignment的问题。值得一提的是，我在实验时发现，ROI Align在VOC2007数据集上的提升效果并不如在COCO上明显。经过分析，造成这种区别的原因是COCO上小目标的数量更多，而小目标受misalignment问题的影响更大（比如，同样是0.5个像素点的偏差，对于较大的目标而言显得微不足道，但是对于小目标，误差的影响就要高很多）。

图 2

图 3

3. ROI Align 的反向传播

常规的ROI Pooling的反向传播公式如下：

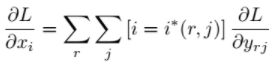
这里，xi代表池化前特征图上的像素点；yrj代表池化后的第r个候选区域的第j个点；i(r,j)代表点yrj像素值的来源（最大池化的时候选出的最大像素值所在点的坐标）。由上式可以看出，只有当池化后某一个点的像素值在池化过程中采用了当前点Xi的像素值（即满足i=i(r，j)），才在xi处回传梯度。

类比于ROIPooling，ROIAlign的反向传播需要作出稍许修改：首先，在ROIAlign中，xi（r,j）是一个浮点数的坐标位置(前向传播时计算出来的采样点)，在池化前的特征图中，每一个与 xi(r,j) 横纵坐标均小于1的点都应该接受与此对应的点yrj回传的梯度，故ROI Align 的反向传播公式如下:

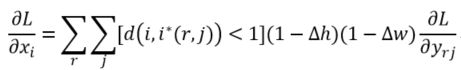
上式中，d(.)表示两点之间的距离，Δh和Δw表示 xi 与 xi*(r,j) 横纵坐标的差值，这里作为双线性内插的系数乘在原始的梯度上。

注：本文系原创文章，转载请注明出处