剪辑自：https://medium.com/huggingface/from-zero-to-research-an-introduction-to-meta-learning-8e16e677f78a#d094

Meta-learning is an exciting trend of research in the machine-learning community which tackles the problem of learning to learn.

The traditional paradigm in machine learning research is to get a huge dataset on a specific task, and train a model from scratch using this dataset. Obviously that’s very far from how humans leverage past experiences to learn very quickly a new task from only a handset of examples.

That’s because humans learn to learn [1].

Over the last months, I have been playing and experimenting quite a lot with meta-learning models for Natural Language Processing and will be presenting some of this work at ICLR, next month in Vancouver 🇨🇦 — come say hi! 👋

In this post, I will start by explaining what’s meta-learning in a very visual and intuitive way. Then, we will code a meta-learning model in PyTorch and I will share some of the lessons learned on this project.

What’s learning in the first place?

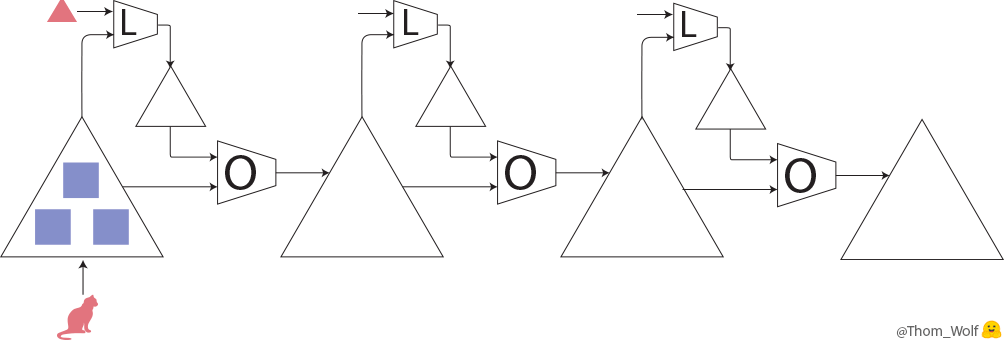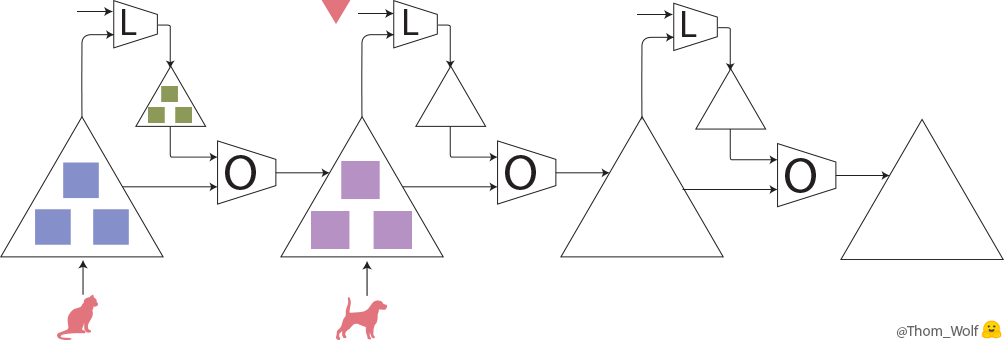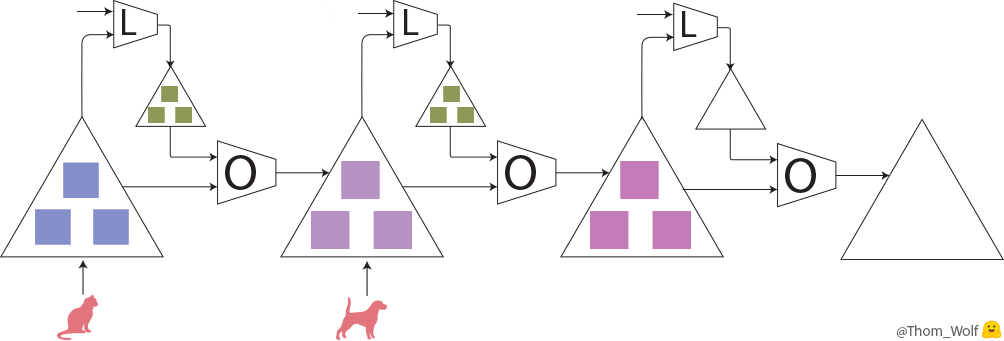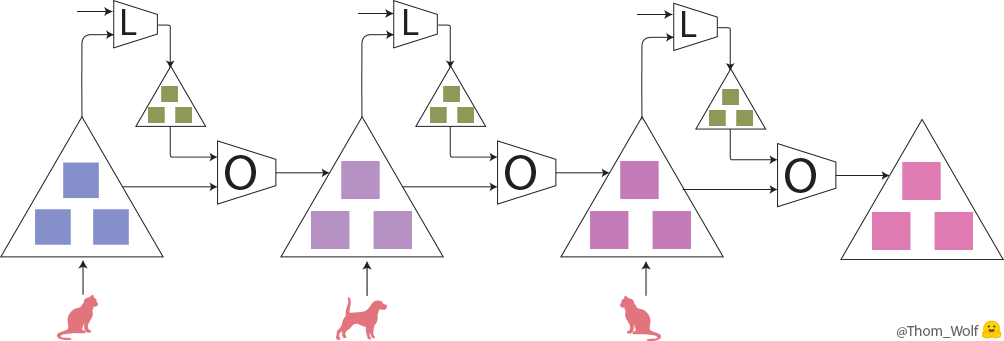
Let’s have a quick look at what happens when we train a simple neural net to classify images of dogs and cats. Let’s say we have a single training image of a cat together with a label indicating that this image represents a cat [2]. I made a quick animation of a training step to save us a few thousand sentences.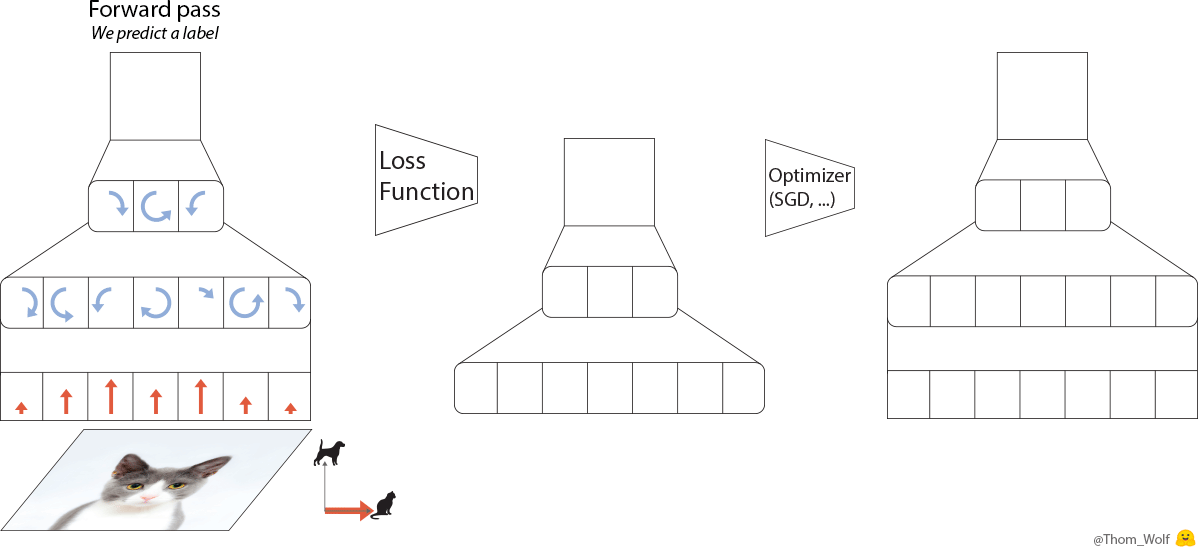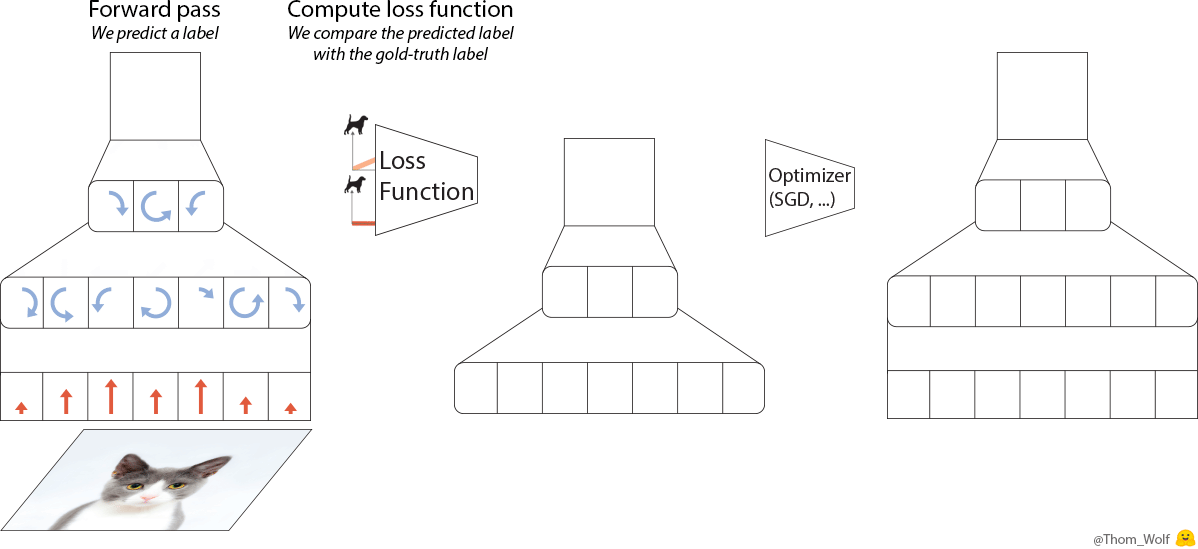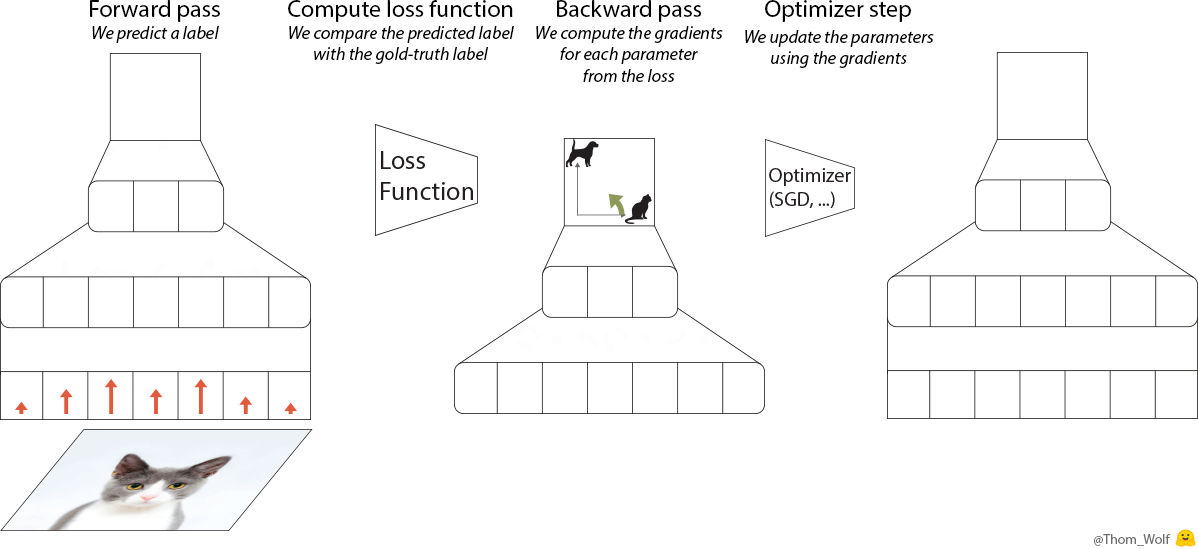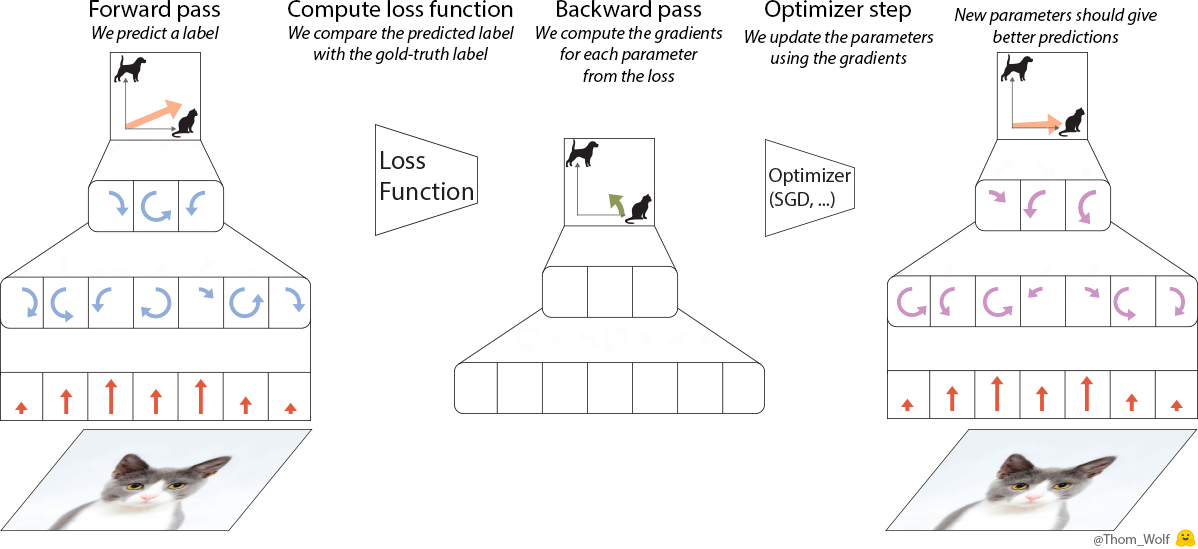

Single step of the training process of a neural network. The neural net is trained to classify an image as representing a dog or a cat

The backward pass (“backprop”) is a key step when we train a neural net. Since the computations performed by the neural network and the loss are differentiable functions [3], we can compute the gradient that should be applied to each parameter of the neural net to reduce the difference between the label currently predicted by the neural net and the real/target label (this difference is measured by the loss function). After the backpropagation comes the optimizer which computes updated parameters for the model. This is where training a neural net becomes more of an art than a science as there are so many possible optimizers and optimization settings (hyper-parameters).

Let’s represent our single training step in a more compact way

The training image is now a 🐈 and the label indicating that the picture represents a cat is a 🔺. Large △s are our neural net with ■ parameters and gradients. The loss function is the L-box and the optimizer the O-box.

The learning process then simply consists in repeatedly applying the optimization step until we converge to good parameters for our neural net.

3 steps of a neural net training process where the neural net (large △s) is trained to classify dogs/cats images.

Let’s turn to meta-learning

The idea of meta-learning is to learn the learning process.

There are several ways to implement meta-learning [4] but the two I want to describe here are about learning a learning process that resemble the one we’ve just seen.

In our training process, there are two things in particular we can learn:

• the initial parameters of the neural net (blue ■) and
• the parameters of the optimizer (pink ★).

I will describe a combination of the two cases but each case is also very interesting on its own and can lead to simplifications, speedups and sound theoretical results [5].

So now, we have two modules to train:

• What I will call the model (M) which is our previous neural net. It can now be seen as a low-level network. It is sometimes called an optimizee or a learner. The weights of the model are the ■ on the drawings.
• The optimizer (O) or meta-learner is a higher-level model which is updating the weights of the lower-level network (the model). The weights of the optimizer are the ★ on the drawings.

How do we learn these meta-parameters?

Well it turns out we can back-propagate a meta-loss gradient along the training process itself, back to the initial weights of the model and/or to the parameters of the optimizer [6].

We now have two, nested, training processes: the meta-training process of the optimizer/meta-learner in which the (meta-)forward pass includes several training steps of the model (with forward, backward and optimization steps as we saw previously).

Let’s take a look at the meta-training step:

A meta-training step (training the optimizer O) comprising with 3 steps of training the model M)

Here, a single step of meta-training process is represented horizontally. It includes two steps of training process of the model (vertically in the meta-forward and meta-backward boxes). The training process of the model is exactly the same training process that we’ve just seen.

As we can see, the input of the meta-forward pass is a list of examples/labels (or a list of batches) that are used successively during the model training pass.

The input of a meta-training step is a list of examples (🐈, 🐕) with associated labels (🔺,🔻)

Now what meta-loss can we use to train the meta-learner? In the case of the model training we could simply compare the model prediction to the target label to get an error signal.

In the case of the meta-learner, we would like a meta-loss that is indicative of how well the meta-learner is performing its task: training the model.

One possibility is then to compute the loss of the model on some training data, the lower the loss, the better the training was. We can compute a meta-loss at the end or even just combine the losses of the model that we already compute during the training (e.g. by summing them).

We also need a meta-optimizer to update the weights of the optimizer. Here it starts to get very meta as we could use another meta-learner to optimize the meta-learner and so on, but in the end we will need a hand-defined optimizer like SGD or ADAM (it can’t be turtles all the way down).

There are a few important remarks regarding the implementation that we can as well discuss now:

• Second-order derivatives: back propagating the meta-loss through the model’s gradients involves computing derivatives of derivative, i.e. second derivatives (when the green ▲ passes through the green ■ on the meta-backward pass of our last animation). We can compute that in modern frameworks like Tensorflow or PyTorch but in practice we often drop the second derivatives and only back propagate though the model weights (the yellow ■ of the meta-backward pass) to reduce the complexity.
• Coordinate sharing: a recent deep-learning model can have a very large number of parameters (easily around 30–200 millions in NLP). With current GPU memory, it is not possible to have such a number of parameters as separate inputs to the optimizer. What we often do is called coordinate-sharing [7], it means we design the optimizer for a single parameter of the model and duplicate it for all parameters (i.e. share it’s weights along the input dimension associated to the model parameters). This way the number of parameters of the meta-learner is not a function of the number of parameters of the model. When the meta-learner is a network with a memory like an RNN, we can still allow to have a separate hidden state for each model parameters to keep separate memories of the evolution of each model parameter.

Meta-learning in PyTorch

Let’s try some code to see how this looks in practice.

So we have a model with a set of weights that we want to train and use for two tasks:

• during the meta-forward pass: we use our model to compute gradients (from the loss) that are feed as inputs to the optimizer to update the model parameters, and
• during the meta-backward pass: we use our model as a path for back propagating the gradients of the optimizer’s parameters (computed from the meta-loss).

The easiest way to do that in PyTorch is to have two duplicate modules that represent the model, one for each task. Let’s call forward model the module responsible for storing the model gradients used during the meta-forward pass and backward model the module responsible for keeping parameters as a continuous path for back propagating the optimizer gradients during the meta-backward pass.

The two modules will share their Tensors to avoid duplicating memory (tensors are the real meat in memory) but will keep separate Variables to cleanly separate the gradients of the model and the gradients used for the meta-learner.

A simple meta-learner class in PyTorch

Sharing Tensors in PyTorch is rather straight-forward: we just need to update the pointers in the Variable class to point to the same Tensors. One difficulty comes when our model is already a memory optimized model like an AWD-LSTM or AWD-QRNN model with shared Tensors (input and output embeddings). Then we need to be careful to keep the right pointers when we update the model parameters of the two modules.

One way to do that is to set a simple helper that will handle the task of looping through the parameters, send back all needed information to update the Parameters pointers (and not only the Tensors) and keep shared parameters synced. Here is such a function:

def get_params(module, memo=None, pointers=None):
    """ Returns an iterator over PyTorch module parameters that allows to update parameters
        (and not only the data).
    ! Side effect: update shared parameters to point to the first yield instance
        (i.e. you can update shared parameters and keep them shared)
    Yields:
        (Module, string, Parameter): Tuple containing the parameter's module, name and pointer
    """
    if memo is None:
        memo = set()
        pointers = {}
    for name, p in module._parameters.items():
        if p not in memo:
            memo.add(p)
            pointers[p] = (module, name)
            yield module, name, p
        elif p is not None:
            prev_module, prev_name = pointers[p]
            module._parameters[name] = prev_module._parameters[prev_name] # update shared parameter pointer
    for child_module in module.children():
        for m, n, p in get_params(child_module, memo, pointers):
            yield m, n, p

Using this function, we can plug any model and loop over the model parameters in our meta-learner in a clean way [8].

Now let’s draft a simple meta-learner class. Our optimizer is a module that will take as inputs during the forward pass, the forward model (with gradients) and the backward model, will loop over their parameters to update the backward model parameter in a way that allows meta-gradients to back propagate (by updating Parameters pointers and not only Tensors).

class MetaLearner(nn.Module):
    """ Bare Meta-learner class
        Should be added: intialization, hidden states, more control over everything
    """
    def __init__(self, model):
        super(MetaLearner, self).__init__()
        self.weights = Parameter(torch.Tensor(1, 2))
    def forward(self, forward_model, backward_model):
        """ Forward optimizer with a simple linear neural net
        Inputs:
            forward_model: PyTorch module with parameters gradient populated
            backward_model: PyTorch module identical to forward_model (but without gradients)
              updated at the Parameter level to keep track of the computation graph for meta-backward pass
        """
        f_model_iter = get_params(forward_model)
        b_model_iter = get_params(backward_model)
        for f_param_tuple, b_param_tuple in zip(f_model_iter, b_model_iter): # loop over parameters
            # Prepare the inputs, we detach the inputs to avoid computing 2nd derivatives (re-pack in new Variable)
            (module_f, name_f, param_f) = f_param_tuple
            (module_b, name_b, param_b) = b_param_tuple
            inputs = Variable(torch.stack([param_f.grad.data, param_f.data], dim=-1))
            # Optimization step: compute new model parameters, here we apply a simple linear function
            dW = F.linear(inputs, self.weights).squeeze()
            param_b = param_b + dW
            # Update backward_model (meta-gradients can flow) and forward_model (no need for meta-gradients).
            module_b._parameters[name_b] = param_b
            param_f.data = param_b.data

We can now train this optimizer as we saw in the first part. Here is a simple gist that illustrate the meta-training process that we have been describing:

def train(forward_model, backward_model, optimizer, meta_optimizer, train_data, meta_epochs):
  """ Train a meta-learner
  Inputs:
    forward_model, backward_model: Two identical PyTorch modules (can have shared Tensors)
    optimizer: a neural net to be used as optimizer (an instance of the MetaLearner class)
    meta_optimizer: an optimizer for the optimizer neural net, e.g. ADAM
    train_data: an iterator over an epoch of training data
    meta_epochs: meta-training steps
  To be added: intialization, early stopping, checkpointing, more control over everything
  """
  for meta_epoch in range(meta_epochs): # Meta-training loop (train the optimizer)
    optimizer.zero_grad()
    losses = []
    for inputs, labels in train_data:   # Meta-forward pass (train the model)
      forward_model.zero_grad()         # Forward pass
      inputs = Variable(inputs)
      labels = Variable(labels)
      output = forward_model(inputs)
      loss = loss_func(output, labels)  # Compute loss
      losses.append(loss)
      loss.backward()                   # Backward pass to add gradients to the forward_model
      optimizer(forward_model,          # Optimizer step (update the models)
                backward_model)
    meta_loss = sum(losses)             # Compute a simple meta-loss
    meta_loss.backward()                # Meta-backward pass
    meta_optimizer.step()               # Meta-optimizer step

Avoid memory blow-up — Hidden State Memorization

Sometimes we want to learn an optimizer that can operate on very large models with several tens of millions of parameters and at the same time we would like to unroll the meta-training over a large number of steps to get good quality gradients [9] like we did in our work.

In practice, it means we want to include a long training process during the meta-forward pass, with many time-steps, and we’ll have to keep in memory the parameters (yellow ■) and gradients (green ■) data for each step that are used for the meta-backward pass.

How can we do that without blowing up our GPU’s memory?

One way is to trade some memory for computation by using gradient checkpointing, also called hidden state memorization [10]. In our case gradient checkpointing consists in slicing the meta-forward and meta-backward passes in segments that we compute successively.

A good introduction to gradient checkpointing is given in the nice blog post of Yaroslav Bulatov of OpenAI. If you are interested in this, you should go and check it:
Fitting larger networks into memory.

This post is already quite long so I won’t include a full gist of gradient checkpointing code. I’ll rather forward you to the nice PyTorch implementation of TSHadley and the current active work to include gradient checkpointing natively in PyTorch.

Other approaches in Meta-learning

There are two other trends of research in meta-learning that I hadn’t time to cover but which are also very promising. I’ll just give you a few pointers so you can go check that for your-self now that you know the general idea:

• Recurrent networks: We have built upon the standard training process of neural nets. An alternative is to consider the succession of task as a sequential series of input and build a recurrent model that can ingest and build a representation of this sequence for a new task. In this case we typically have a single training process with a recurrent network with memory or attention. This approach also gives good results, in particular when the embeddings are adequately designed for the task. A good example is the recent SNAIL paper.
• Reinforcement learning: The computation made by the optimizer during the meta-forward pass is very similar to the computation of a recurrent network: repeatedly apply the same parameters on a sequence of inputs (the succession of weights and gradients of the model during the learning). In practice this means we meet a usual issue with recurrent nets: the models have trouble returning to a safe path when they make errors as they are not trained to recover from training errors and the models have difficulties generalizing to longer sequences than the ones used during the meta-training. To tackle these issues, one can turn to reinforcement learning approaches where the model learn an action policy associated to a current state of training.

There is an interesting parallel between meta-learning and neural net models used in Natural Language Processing (NLP) like recurrent neural networks (RNN) that we have just started mentioning in the previous paragraph:

A meta-learner optimizing a neural net model behaves similarly to a recurrent neural network.

Like an RNN, the meta-learner ingests a series of parameters and gradients of the model during training, as an input sequence, and compute a sequential output (the series of updated model parameters) from this input sequence.

We develop this analogy in our paper and study how a meta-learner can be used to implement a medium-term memory in a neural net language model: the meta-learner learns to encode a medium-term memory in the weights of a standard RNN like a LSTM (in addition to the way short-term memories are conventionally encoded in the hidden state of the LSTM).

Our meta-learning language model has a hierarchy of memories with 3 levels, from bottom to top: a standard LSTM, a meta-learner updating the weights of the LSTM to store medium term memories and a long-term static memory.

We discovered that the meta-learning language model could be trained to encode memory of recent inputs, like the beginning of a Wikipedia article, that will be useful to predict the end of an article.

The curves indicate how good the model is at predicting the words of a Wikipedia article given the beginning (A, …, H are successive Wikipedia articles), colored words indicate the same for single words, blue is better, red is worse. As the model reads through an article, it learns from the beginning and become better at predicting the end (for more details see our paper).

Well I guess now you are ready to have a look at our paper for more details on this story.

This concludes my introduction to Meta-Learning. Congratulation for reaching the end of this long post!

I hope you liked it!

Don’t forget to give us a few claps 👏 if you want more content like that!

1. ^ As such, meta-learning can be seen as a generalization of “transfer learning” and is related to the techniques for fine-tuning model on a task as well as techniques for hyper-parameters optimization. There was an interesting workshop on meta-learning at NIPS 2017 last December.
2. ^ Of course in a real training we would be using a mini-batch of examples.
3. ^ More precisely: “most of” these operations are differentiable.
4. ^ Good blog posts introducing the relevant literature are the BAIR posts: Learning to learn by Chelsea Finn and Learning to Optimize with Reinforcement Learning by Ke Li.
5. ^ Good examples of learning the model initial parameters are Model-Agnostic Meta-Learning of UC Berkeley and its recent developments as well as the Reptile algorithm of OpenAI. A good example of learning the optimizer’s parameters is the Learning to learn by gradient descent by gradient descent paper of DeepMind. A paper combining the two is the work Optimization as a Model for Few-Shot Learning by Sachin Ravi and Hugo Larochelle. An nice and very recent overview can be found in Learning Unsupervised Learning Rules.
6. ^ Similarly to the way we back propagate through time in an unrolled recurrent network.
7. ^ Initially described in DeepMind’s Learning to learn by gradient descent by gradient descent paper.
8. ^ We are using coordinate-sharing in our meta-learner as mentioned earlier. In practice, it means we simply iterate over the model parameters and apply our optimizer broadcasted on each parameters (no need to flatten and gather parameters like in L-BFGS for instance).
9. ^ There is a surprising under-statement of how important back-propagating over very long sequence can be to get good results. The recent paper An Analysis of Neural Language Modeling at Multiple Scales from Salesforce research is a good pointer in that direction.
10. ^ Gradient checkpointing is described for example in Memory-Efficient Backpropagation Through Time and the nice blog post of Yaroslav Bulatov.